Probabilidad teórica: cómo sacarla, ejemplos, ejercicios
La probabilidad teórica (o de Laplace) de que ocurra un evento E que pertenece a un espacio muestral S, en el que todos los eventos tienen igual probabilidad de ocurrencia, se define en notación matemática como: P(E) = n(E) / N(S)
Donde P(E) es la probabilidad, dada como el cociente entre el número total de posibles resultados del evento E, al cual llamamos n(E), dividido entre el número total N(S) de posibles resultados en el espacio muestral S.

La probabilidad teórica es un número real comprendido entre 0 y 1, pero frecuentemente se expresa en forma de porcentaje, en cuyo caso la probabilidad será un valor comprendido entre 0% y 100%.
Calcular la probabilidad de ocurrencia de un evento es muy importante en muchos campos, tales como la actividad bursátil, las compañías de seguros, los juegos de azar y muchos más.
Índice del artículo
Un caso ilustrativo es el caso de las rifas o loterías. Suponga que se emiten 1.000 boletos para rifar un teléfono inteligente. Como el sorteo se hace en forma aleatoria, cualquiera de los boletos tiene igual posibilidad de ser ganador.
Para hallar la probabilidad de que una persona que compra un boleto con el número 81 sea ganadora, se efectúa el siguiente cálculo de probabilidad teórica:
P(1) = 1/1.000 = 0,001 = 0,1%
El resultado anterior se interpreta de la siguiente manera: si el sorteo se repitiese infinitas veces, cada 1.000 veces el boleto 81 sería seleccionado, en promedio, una vez.
Si por algún motivo alguien adquiere todos los boletos es seguro que ganará el premio. La probabilidad de ganar el premio si se tienen todos los boletos se calcula así:
P(1.000) = 1.000/1.000 = 1 = 100%.
Es decir, que probabilidad 1 o 100% significa que es totalmente seguro que ese resultado ocurrirá.
Si alguien posee 500 boletos las posibilidades de ganar o perder son las mismas. La probabilidad teórica de ganar el premio en este caso se calcula así:
P(500) = 500/1.000 = ½ = 0,5 = 50%.
Aquel que no compra ningún boleto no tiene ninguna posibilidad de ganar y su probabilidad teórica se determina así:
P(0) = 0 / 1.000 = 0 = 0%
Se tiene una moneda con cara en un lado y escudo o sello en el otro. Cuando se lanza la moneda ¿Cuál es la probabilidad teórica de que salga cara?
P(cara) = n(cara) / N( cara + escudo ) = ½ = 0,5 = 50%
El resultado se interpreta de la siguiente manera: si se hiciese un número enorme de lanzamientos, en promedio en cada 2 lanzamientos uno de ellos saldría cara.
En términos porcentuales, la interpretación del resultado es que realizando un número infinitamente grande de lanzamientos, en promedio de cada 100 de ellos 50 darían como resultado cara.
En una caja hay 3 canicas azules, 2 canicas rojas y 1 verde. ¿Cuál es la probabilidad teórica de que al sacar una canica de la caja esta sea roja?
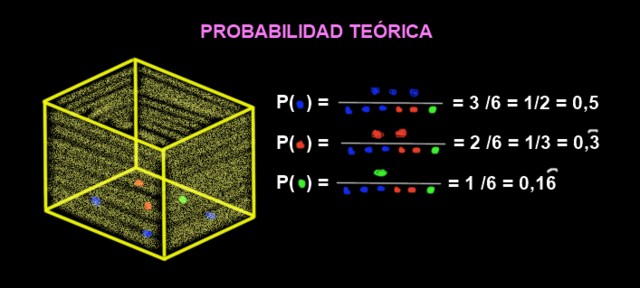
La probabilidad que salga roja es:
P(roja) = Número de casos favorables / Número de casos posibles
Es decir:
P(roja) = Número de canicas rojas / Número total de canicas
Finalmente se tiene que la probabilidad que se extraiga una canica roja es:
P(roja) = 2 / 6 = ⅓ = 0,3333 = 33,33%
Mientras que la probabilidad que al extraer una canica verde es:
P(verde) = ⅙ = 0,1666 = 16,66%
Por último, la probabilidad teórica de obtener en una extracción a ciegas una canica azul es:
P(azul) = 3/6 = ½ = 0,5 = 50%
Es decir, de cada 2 intentos el resultado será azul en uno de ellos y otro color en otro intento, bajo la premisa de que se repone la canica extraída y que el número de ensayos es muy, muy grande.
Determinar la probabilidad de que al lanzar un dado se obtenga un valor menor o igual a 4.
Solución
Para calcular la probabilidad de que ocurra este evento se aplicará la definición de probabilidad teórica:
P(≤4) = Número de casos favorables / Número de casos posibles
P(≤5) = 5 / 6 = = 83,33%
Hallar la probabilidad de que en dos lanzamientos consecutivos de un dado normal de seis caras salga 5 las 2 veces.
Solución
Para dar respuesta a este ejercicio conviene hacer un cuadro para mostrar todas las posibilidades. La primera cifra indica el resultado del primer dado y la segunda el resultado del otro.

Para calcular la probabilidad teórica necesitamos conocer el número total de casos posibles, en este caso como puede verse del cuadro anterior, hay 36 posibilidades.
También observando el cuadro se deduce que el número de casos favorables al evento que en los dos lanzamientos consecutivos salga 5 es solamente 1, resaltado con color, por lo tanto la probabilidad de que este evento ocurra es:
P(5 x 5) = 1 / 36.
También se pudo haber llegado a este resultado usando una de las propiedades de la probabilidad teórica, la cual afirma que la probabilidad combinada de dos eventos independientes es el producto de sus probabilidades individuales.
En este caso la probabilidad de que en el primer lanzamiento salga 5 es ⅙. El segundo lanzamiento es completamente independiente del primero, por tanto la probabilidad que salga 5 en el segundo es también ⅙. Entonces la probabilidad combinada es:
P(5×5) = P(5) P(5) = (1/6) (1/6) = 1/36.
Hallar la probabilidad que en el primer lanzamiento salga un número menor que 2 y en el segundo salga un número mayor que 2.
Solución
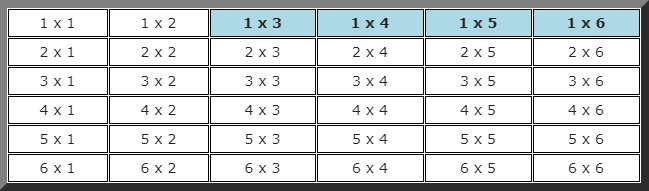
Nuevamente hay que construir una tabla de eventos posibles, donde se subrayan aquellos en los cuales el primer lanzamiento resultó menor a 2 y en el segundo mayor a 2.
En total hay 4 posibilidades de un total de 36. Es decir que la probabilidad de este evento es:
P(2 ; >2) = 4 / 36 = 1/9 = 0,1111 = 11,11%
Usando el teorema de probabilidades que afirma:
La probabilidad de ocurrencia de dos eventos independientes es igual al producto de las probabilidades individuales.
Se obtiene idéntico resultado:
P(2) P(>2) = (1/6) (4/6) = 4 / 36 = 0,1111 = 11,11%
El valor obtenido con este procedimiento coincide con el resultado anterior, mediante la definición teórica o clásica de la probabilidad.
Cual es la probabilidad que al lanzar dos dados la suma de los valores sea 7.
Solución

Para hallar la solución en este caso se ha elaborado un cuadro de posibilidades en el que se ha indicado en color los casos que cumplen la condición de que la suma de los valores sea 7.
Mirando la tabla pueden contarse 6 casos posibles, por lo que la probabilidad es:
P( I + II : 7) = 6 / 36 = 1/6 = 0,1666 = 16,66%
- Canavos, G. 1988. Probabilidad y Estadística: Aplicaciones y métodos. McGraw Hill.
- Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
- Lipschutz, S. 1991. Serie Schaum: Probabilidad. McGraw Hill.
- Obregón, I. 1989.Teoría de la probabilidad. Editorial Limusa.
- Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.
