Capacitancia: unidades, fórmulas, cálculo, ejemplos
La capacitancia es la relación que existe entre la carga de un condensador o capacitador, medido en coulomb, y su potencial eléctrico o voltaje, medido en voltios. Se expresa en unidades faradio (F), en honor a Michael Faraday (1791-1867).
La capacitancia también es definida como la propiedad o capacidad de un condensador o conjunto de condensadores eléctricos, que se mide por la cantidad de carga eléctrica que pueden almacenar, en forma separada, por unidad de cambio del potencial eléctrico.

El término capacitancia es introducido como consecuencia de la creación de un dispositivo eléctrico llamado capacitor, inventado por el científico prusiano Ewald Georg von Kleist, en 1745, e independientemente por el físico holandés Pieter van Musschenbroek.
Los capacitores son dispositivos eléctricos que almacenan carga eléctrica y la descargan en forma instantánea. Esta propiedad ha sido utilizada en numerosos aparatos eléctricos, como la televisión, el radio, las lámparas, la computadora, entre otros muchos de la vida cotidiana.
Índice del artículo
- 1 Capacitor y capacitancia
- 2 Unidades y fórmulas
- 3 ¿Cómo se calcula la capacitancia?
- 4 Ejemplos
- 5 Ejercicios resueltos
- 6 Combinación de capacitores
- 7 Referencias
Un condensador o capacitor está formado por dos conductores que tienen cargas iguales y de signo contrario. Los conductores se denominan armaduras o placas del condensador.
Una placa está unida al borne positivo (+) de una batería, mientras la otra placa está unida al negativo (-). Como las placas tienen cargas iguales y de signo contrario, la carga neta de un capacitor es de cero (0).
La capacitancia es la relación entre la carga de un conductor o conductores que forman un capacitor y el valor de la diferencia de voltaje existente entre las placas del condensador.
La fórmula de la capacitancia es la siguiente:
C = q / v
Donde C es capacitancia, q la carga (cuya unidad es el coulomb) y v el voltaje (voltio)
La unidad de capacitancia es el faradio (F), el cual equivale a coulomb / voltio. El faradio es una unidad muy grande, por lo que se utiliza el microfaradio (µF), que equivale a 10-6 faradio; o el pico faradio (pF), que equivale a 10-12 faradio.
¿Cuál será el valor de la capacitancia de un capacitor cuyas placas tienen una carga de 5·10-3 coulomb, y una diferencia de voltaje de 6 voltios?
Aplicando la fórmula resolvemos:
C = q / v
= (5·10-3 coulomb) / (6 volt)
= 8,33·10-4 faradio
La fórmula de la capacitancia varía dependiendo del tipo de capacitor.
C = kεoA / d
k es la constante dieléctrica, la cual tiene un valor de 1 en el aire y el vacío. Por esta razón la fórmula se reduce a:
C = εoA / d
εo es la constante de dieléctrica, cuyo valor es cercano a 8,854·10-12 F·m-1, A es el área o superficie de las placas en paralelo expresada en m2, mientras d la distancia que separa las placas paralelas.
C = 4ΠεoR
Donde R es el radio de la esfera en metros.
C = 4Πεo / (1/R1 – 1/R2)
C = 2Πεol/ln (R2 / R1)
Donde l es la longitud de los cilindros concéntricos en metros.
¿Cuál será la capacidad de un capacitor o condensador en el aire con un área de sus placas de 3 cm2 y separadas por una distancia de 2 mm?
Tenemos la fórmula:
C = εoA/d
Y los datos:
εo = 8,854 x 10-12 F·m-1
A = 3 cm2 (3·10-4 m2)
d = 2 mm (2·10-3 m)
Se procede simplemente a sustituir:
C = (8,854·10-12 F·m-1)(3·10-4 m2) / (2·10-3 m)
= 1,3281·10-14 F
Si se considera a la Tierra como un capacitor esférico con un radio (R) de 6.370 km: ¿Cuál será el valor de su capacitancia?
Datos:
C = 4ΠεoR
Π = 3,1416
εo = 8,854·10-12 F.m-1
R = 6.370 Km (6,37·106 m)
Se procede nuevamente a sustituir los valores en la fórmula de la capacitancia:
C = (4·3,1416)(8,854·10-12 F·m-1)(6,37·106 m)
= 7,09·10-8 F
= 709 µF
Los capacitores o condensadores se pueden combinar en serie o en paralelo.
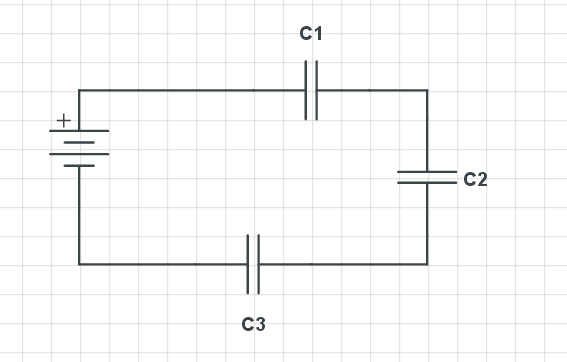
La imagen superior muestra tres capacitores en serie (C1, C2 y C3), así como una batería con sus bornes positivo (+) y negativo (-). Estos capacitores presentan una serie de características en relación a su voltaje, carga y capacitancia.
Caída de voltaje (ΔV) en los capacitores
ΔVt = ΔV1 + ΔV2 + ΔV3
La caída total de voltaje en un conjunto de capacitores en serie es igual a la suma de las caídas de voltaje de los capacitores.
Carga de los capacitores
Qt = Q1 = Q2 = Q3
Por los capacitores dispuestos en serie circula la misma cantidad de carga.
Capacitancia de los capacitores
La capacitancia equivalente de los capacitores en serie presenta la siguiente relación:
1/Ceq = 1/C1 + 1/C2 + 1/C3
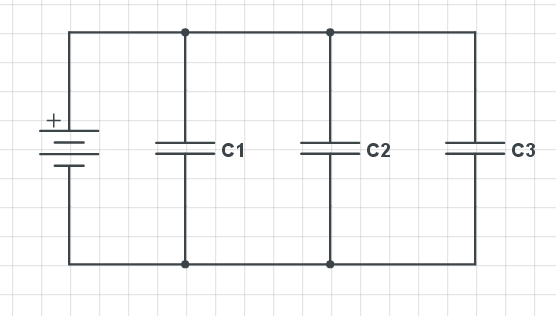
Arriba tenemos tres capacitores dispuestos en paralelo (C1, C2 y C3), los cuales guardan en relación a la caída de voltaje, la carga y la capacitancia el comportamiento siguiente:
Caída de voltaje en los capacitores
ΔVt = ΔV1 = ΔV2 = ΔV3
En los capacitores en paralelo la caída de voltaje total de los capacitores es la misma que la existente para cada uno de los capacitores.
Carga de los capacitores
Qt = Q1 + Q2 + Q3
En un sistema en paralelo la carga total de los capacitores es igual a la suma de la carga de todos los capacitores.
Capacitancia de los capacitores
Ceq = C1 + C2 + C3
En un sistema en paralelo la capacitancia equivalente de ellos es igual a la suma de las capacitancias de todos los capacitores.
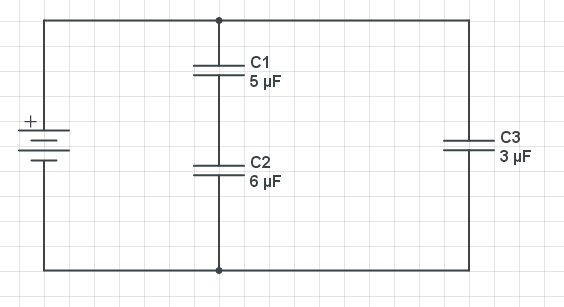
Arriba se muestra un esquema de tres capacitores: C1 y C2 están dispuestos en serie y ellos están en paralelo con C3. La capacitancia de los capacitores son las siguientes: C1 = 5 µF, C2 = 6 µF y C3 = 3 µF. Hallar la capacitancia equivalente del circuito.
Primero se halla la capacitancia equivalente de C1 y C2 que están en serie.
1/Ceq1,2 = 1/C1 + 1/C2
1/Ceq1,2 = 1/5 µF + 1/6 µF
1/Ceq1,2 = (11 / 30) µF
Ceq1,2 = 30 µF / 11
= 2,72 µF
Los capacitores 1 y 2 están en paralelo con C3. Entonces, la capacitancia equivalente de C1, C2 y C3 es igual a Ceq1,2 + C3.
Ceq1,2,3 = 2,72 µF + 3 µF
= 5,72 µF
- Serway, R. A. y Jewett, J. W. (2009). Física para ciencias e ingeniería. Volumen 2. Séptima Edición. Editorial Cengage Learning.
- Reddick, R y Halliday, D. (1965). Física. Parte 2. Segunda edición en español. Editorial Continental S.A.
- Study. (22 de abril de 2015). Capacitance: Units & Formula. Recuperado de: study.com
- Lumen Physics. (s.f.). Capacitors in Series and Parallel. Recuperado de: courses.lumenlearning.com
- The Editors of Encyclopaedia Britannica. (2020). Capacitance. Recuperado de: britannica.com
