¿Qué es un experimento determinista?
El experimento determinista, en estadística, es aquel que tiene un resultado predecible y reproducible siempre que se mantengan las mismas condiciones y parámetros iniciales. Es decir, la relación causa-efecto es conocida en su totalidad.
Por ejemplo, el tiempo que le toma a la arena de un reloj en pasar de un compartimiento al otro es un experimento determinista, porque el resultado es predecible y reproducible. Siempre y cuando las condiciones sean las mismas, tardará el mismo tiempo en desplazarse de cápsula a cápsula.

Muchos fenómenos físicos son deterministas, siendo algunos ejemplos los siguientes:
– Un objeto más denso que el agua, como una piedra, siempre se hundirá.
– Un flotador, que es menos denso que el agua, siempre saldrá a flote (a menos que se ejerza una fuerza que lo mantenga sumergido).
– La temperatura de ebullición del agua a nivel del mar siempre es 100 ºC.
– El tiempo que tarda en caer un dado que se deja caer del reposo, ya que está determinado por la altura desde la que se dejó caer y este tiempo siempre es igual (cuando se suelta desde la misma altura).
Aprovechando el ejemplo del dado. Si este se deja caer, aun cuando se tenga el cuidado de darle la misma orientación y siempre a la misma altura, es difícil predecir qué cara mostrará hacia arriba una vez que se haya detenido en el suelo. Esto sería un experimento aleatorio.
Teóricamente, si se conocieran con precisión infinita datos como: posición; velocidad inicial y orientación del dado; forma (de bordes redondeados o angulosos); y coeficiente de restitución de la superficie sobre la que cae, tal vez sería posible predecir, mediante cálculos complejos, qué cara mostrará hacia arriba el dado cuando se detenga. Pero cualquier variación ínfima en las condiciones de partida daría un resultado diferente.
Tales sistemas son deterministas y a la vez caóticos, ya que una pequeña alteración de las condiciones iniciales cambia el resultado final de forma aleatoria.
Índice del artículo
Los experimentos deterministas son completamente medibles, pero aun así la medición de su resultado no es infinitamente precisa y tiene cierto margen de incertidumbre.
Pongamos por ejemplo el siguiente experimento, totalmente determinista: soltar un auto de juguete por un pista recta inclinada.

Siempre se suelta desde el mismo punto de partida, teniendo el cuidado de no dar ningún impulso. En este caso, el tiempo que le toma al auto recorrer la pista debe ser siempre el mismo.
Ahora un niño se propone medir el tiempo que le toma al carrito recorrer la pista. Para esto usará el cronómetro que viene incorporado a su teléfono móvil.
Siendo un chico observador, lo primero que nota es que su instrumento de medida tiene una precisión finita, porque la menor diferencia de tiempo que puede medir el cronómetro es de 1 centésima de segundo.
Luego el niño procede a realizar el experimento y con el cronómetro del móvil mide 11 veces -digamos que para estar bien seguro- el tiempo que le tomó al cochecito recorrer el plano inclinado, obteniendo los siguientes resultados:
3,12s 3,09s 3,04s 3,04s 3,10s 3,08s 3,05s 3,10s 3,11s 3,06s y 3,03s.
El niño se sorprende, porque en la escuela le habían dicho que este es un experimento determinista, pero en cada medida obtuvo un resultado ligeramente diferente.
¿Cuáles pueden ser las causas que en cada medición se tenga un resultado diferente?
Una causa puede ser la precisión del instrumento, que como ya se había dicho es de 0,01s. Pero nótese que las diferencias en las mediciones están por encima de ese valor, por lo que debe pensarse en otras causas, como por ejemplo:
– Pequeñas variaciones del punto de partida.
– Diferencias en el inicio y pausa del cronómetro, debido al tiempo de reacción del niño.
Respecto al tiempo de reacción ciertamente ocurre un retardo desde que el niño ve que se comienza a mover el carrito, hasta que pulsa el cronómetro.
Similarmente, en la llegada hay un retardo debido al tiempo al tiempo de reacción. Pero los retardos de inicio y llegada se compensan, de modo que el tiempo obtenido debe ser muy cercano al verdadero.
En todo caso, la compensación por el retardo de reacción no es exacta, porque los tiempos de reacción pueden tener pequeñas variaciones en cada ensayo, lo cual explica las diferencias en los resultados.
¿Cuál es entonces el verdadero resultado del experimento?
Para reportar el resultado final debemos echar mano de la estadística. Primero veamos con qué frecuencia se repiten los resultados:
– 3,03s (1 vez)
– 3,04s (2 veces)
– 3,05s (1 vez)
– 3,06s (1 vez)
– 3,08s (1 vez)
– 3,09s 1 vez
– 3,10s (2 veces)
– 3,11s (1 vez)
– 3,12s (1 vez)
Al ordenar los datos, nos damos cuenta que no puede precisarse una moda o resultado más repetido. Entonces el resultado a reportar es la media aritmética, que puede calcularse así:
(1×3,03 + 2×3,04 + 1×3,05 + 1x 3,06 + 1×3,08 + 1×3,09 + 2×3,10 + 1×3,11 + 1×3,12) / (1 + 2 + 1 + 1 + 1 + 1 + 2 + 1 + 1).
El resultado del cálculo anterior es 3,074545455. Lógicamente no tiene sentido reportar en el resultado todos estos decimales, debido a que cada medición tiene nada más 2 decimales de precisión.
Aplicando las reglas de redondeo, puede afirmarse que el tiempo que le toma al carrito recorrer la pista es la media aritmética redondeada a dos cifras decimales.
El resultado que podemos reportar para nuestro experimento es:
3,08 segundos es el tiempo que le toma al carro de juguete recorrer la pista inclinada.
Como se ha visto en nuestro ejemplo de experimento determinista, toda medición tiene un error, puesto que no puede medirse con precisión infinita.
En todo caso, lo único que puede hacerse es mejorar los instrumentos y los métodos de medición, con el fin de obtener un resultado más preciso.
En la sección anterior dimos un resultado para nuestro experimento determinista del tiempo que le toma al coche de juguete recorrer una pista inclinada. Pero este resultado lleva implícito un error. Ahora explicaremos cómo calcular ese error.
En las mediciones para el tiempo se nota una dispersión en la medidas realizadas. La desviación estándar es una forma usada frecuentemente en estadística para reportar la dispersión de los datos.
Varianza y desviación estándar
La forma de calcular la desviación estándar es así: primero se encuentra la varianza de los datos, definida de esta forma:
La suma de las diferencias de cada resultado con la media aritmética, elevada al cuadrado y dividido entre el número total de datos
Si a la varianza se le toma la raíz cuadrada, se obtiene entonces la desviación estándar.
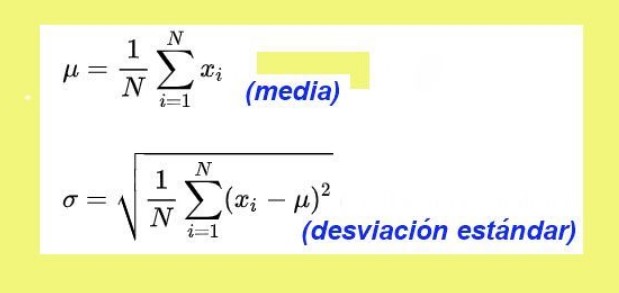
La desviación estándar para los datos del tiempo de descenso del autito de juguete es:
σ = 0,03
El resultado fue redondeado a 2 decimales, porque la precisión de cada uno de los datos es de 2 decimales. En este caso 0,03s representa el error estadístico de cada uno de los datos.
Sin embargo, el promedio o media aritmética de los tiempos obtenidos tiene un error menor. El error del promedio se calcula dividiendo la desviación estándar entre la raíz cuadrada del número total de datos.
Error del promedio = σ / √N = 0,03 / √11= 0,01
Es decir, el error estadístico del promedio de tiempo es 1 centésima de segundo y en este ejemplo, coincide con la apreciación del cronómetro, pero no siempre es así.
Como resultado final de la medida, se reporta entonces:
t = 3,08s ± 0,01s es el tiempo que le toma al coche de juguete recorrer la pista inclinada.
Se concluye que aun cuando se trata de un experimento determinista, el resultado de su medición no tiene precisión infinita y siempre tiene un margen de error.
Y además, para reportar el resultado final es necesario, aun cuando se trata de un experimento determinista, usar métodos estadísticos.
- CanalPhi. Experimento determinista. Recuperado de: youtube.com
- MateMovil. Experimento determinista. Recuperado de: youtube.com
- Pishro Nick H . Introduction to probability. Recuperado de: probabilitycourse.com
- Ross. Probabilidad y estadistica para ingenieros. Mc-Graw Hill.
- Statistic how to. Deterministic: Definition and Examples. Recuperado de: statisticshowto.datasciencecentral.com
- Wikipedia. Desviación típica. Recuperado de: es.wikipedia.com
- Wikipedia. Experiment (probability theory). Recuperado de: en.wikipedia.com
