Teorema de existencia y unicidad: demostración, ejemplos y ejercicios
El teorema de existencia y unicidad establece las condiciones necesarias y suficientes para que una ecuación diferencial de primer orden, con condición inicial dada, tenga una solución y que además dicha solución sea la única.
Sin embargo el teorema no da ninguna técnica ni indicación de cómo hallar tal solución. El teorema de existencia y unicidad se extiende también a ecuaciones diferenciales de orden superior con condiciones iniciales, lo que se conoce como problema de Cauchy.
El enunciado formal del teorema de existencia y unicidad es el siguiente:
“Para una ecuación diferencial y’(x) = f(x,y) con condición inicial y(a) = b, existe al menos una solución en una región rectangular del plano XY que contiene al punto (a,b), si f(x,y) es continua en dicha región. Y si la derivada parcial de f respecto de y: g = ∂f/ ∂y es continua en esa misma región rectangular, entonces la solución es única en un entorno del del punto (a,b) contenido en la región de continuidad de f y g.”
La utilidad de este teorema radica primero en conocer cuáles son las regiones del plano XY en las que puede existir una solución y además, saber si la solución encontrada es la única posible o si existen otras.
Nótese que en caso de que no se cumpla la condición de unicidad, el teorema no puede predecir cuántas soluciones en total tiene el problema de Cauchy: tal vez sea una, dos, o más.
Índice del artículo

Para este teorema se conocen dos demostraciones posibles, una de ellas es la demostración de Charles Émile Picard (1856-1941) y la otra se debe a Giuseppe Peano (1858-1932) basado en los trabajos de Augustin Louis Cauchy (1789-1857).
Es de notar que en la demostración de este teorema participaron las mentes matemáticas más brillantes del siglo XIX, por lo que se puede intuir que ninguna de las dos es sencilla.
Para demostrar formalmente el teorema se requiere establecer primero una serie de conceptos de matemáticas más avanzadas, como funciones tipo Lipschitz, espacios de Banach, teorema de existencia de Carathéodory y varios más, que escapan del propósito del artículo.
Una gran parte de las ecuaciones diferenciales que se manejan en física tratan con funciones continuas en las regiones de interés, por lo tanto nos limitaremos a mostrar la forma en que se aplica el teorema en ecuaciones sencillas.
Consideremos la siguiente ecuación diferencial con una condición inicial:
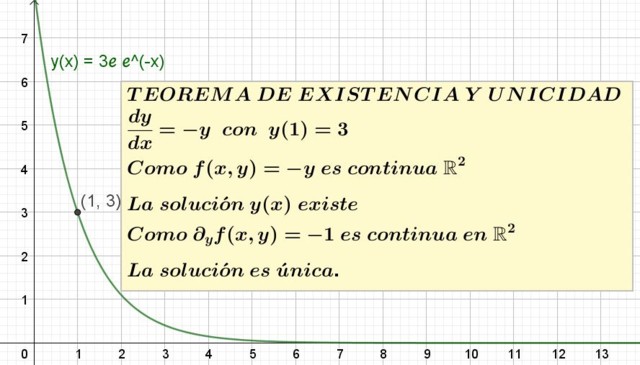
y’(x) = – y; con y(1) =3
¿Existe una solución para este problema? ¿Es la única solución posible?
Respuestas
En primer lugar se evalúa la existencia de la solución de la ecuación diferencial y que además que cumpla la condición inicial.
En este ejemplo f(x,y) = – y la condición de existencia requiere saber si f(x,y) es continua en una región del plano XY que contenga al punto de coordenadas x=1, y=3.
Pero f(x,y)=-y es la función afín, que es continua en el dominio de los números reales y existe en todo el rango de los números reales.
Por lo tanto se concluye que f(x,y) es continua en R2, por lo que el teorema garantiza la existencia de al menos una solución.
Sabiendo esto, toca evaluar si la solución es única o si por el contrario hay más de una. Para esto es necesario calcular la derivada parcial de f respecto de la variable y:
∂f/∂y = ∂(-y)/∂y = -1
Entonces g(x,y) = -1 que es una función constante, que también está definida para todo R2 y además es continua allí. Se sigue que el teorema de existencia y unicidad garantiza que este problema de valor inicial sí tiene una solución única, aunque no nos dice cuál es.
Considere la siguiente ecuación diferencial ordinaria de primer orden con condición inicial:
y’(x) = 2√y ; y(0) = 0.
¿Existe una solución y(x) para este problema? En caso afirmativo determinar si hay una o más de una.
Respuesta
Consideramos la función f(x,y) = 2√y. La función f está definida únicamente para y≥0, pues sabemos que un número negativo carece de raíz real. Además f(x,y) es continua en el semiplano superior de R2 incluido el eje X, por lo que el teorema de existencia y unicidad garantiza al menos una solución en dicha región.
Ahora bien, la condición inicial x=0,y=0 está en el borde de la región de solución. Entonces tomamos la derivada parcial de f(x,y) respecto de y:
∂f/∂y = 1/√y
En este caso la función no está definida para y=0, precisamente donde está la condición inicial.
¿Qué nos dice el teorema? Nos dice que aunque sabemos que existe al menos una solución el semiplano superior del eje X incluido el eje X, como no se cumple la condición de unicidad, no hay garantía que exista una solución única.
Esto significa que podría haber una o más de una solución en la región de continuidad de f(x,y). Y como siempre, el teorema no nos dice cuáles podrían ser.
Resolver el problema de Cauchy del ejemplo 1:
y’(x) = – y; con y(1) =3.
Hallar la función y(x) que satisface la ecuación diferencial y la condición inicial.
Solución
En el ejemplo 1 se determinó que este problema tiene solución y además es única. Para encontrar la solución, lo primero que debe notarse es que se trata de una ecuación diferencial de primer grado de variables separables, la cual se escribe de la siguiente manera:
dy /dx = – y → dy = -y dx
Dividiendo entre y en ambos miembros para separar las variables nos queda:
dy/y = – dx
Se aplica la integral indefinida en ambos miembros:
∫(1/y) dy = – ∫dx
Resolviendo las integrales indefinidas se tiene:
ln(y) = -x + C
donde C es una constante de integración que se determina mediante la condición inicial:
ln(3) = -1 + C, es decir que C = 1 + ln(3)
Sustituyendo el valor de C y reorganizando queda:
ln(y) – ln(3) = -x + 1
Aplicando la siguiente propiedad de los logaritmos:
La diferencia de logaritmos es el logaritmo del cociente
La expresión anterior puede reescribirse así:
ln(y/3) = 1 – x
Se aplica la función exponencial con base e en ambos miembros para obtener:
y / 3 = e(1 – x)
Que equivale a:
y = 3e e-x
Esta es la solución única de la ecuación y’ = -y con y(1) = 3. El gráfico de dicha solución se muestra en la figura 1.
Hallar dos soluciones para el problema planteado en el ejemplo 2:
y’(x) = 2√(y) ; y(0) = 0.
Solución
También se trata de una ecuación de variables separables, que escrita en forma diferencial queda así:
dy / √(y) = 2 dx
Tomando la integral indefinida en ambos miembros queda:
2 √(y)= 2 x + C
Como se sabe que y≥0 en la región de solución nos queda:
y = (x + C)2
Pero como debe cumplirse la condición inicial x=0, y=0, entonces la constante C es cero y queda la siguiente solución:
y(x) = x2.
Pero esta solución no es única, la función y(x) = 0 también es solución del problema planteado. El teorema de existencia y unicidad aplicado a este problema en el ejemplo 2 ya había predicho que podía existir más de una solución.
- Coddington, Earl A.; Levinson, Norman (1955), Theory of Ordinary Differential Equations, New York: McGraw-Hill.
- Encyclopedia of Mathematics. Cauchy-Lipschitz theorem. Recuperado de: encyclopediaofmath.org
- Lindelöf, Sur l’application de la méthode des approximations successives aux équations différentielles ordinaires du premier ordre; Comptes rendus hebdomadaires des séances de l’Académie des sciences. Vol. 116, 1894, pp. 454–457. Recuperado de: gallica.bnf.fr.
- Wikipedia. Método de las aproximaciones sucesivas de Picard. Recuperado de: es.wikipedia.com
- Wikipedia. Teorema de Picard-Lindelöf. Recuperado de: es.wikipedia.com.
- Zill, D.1986. Ecuaciones diferenciales elementales con Aplicaciones.Prentice Hall.
