Factor común por agrupación de términos: ejemplos, ejercicios
El factor común por agrupación de términos es un procedimiento algebraico que permite escribir algunas expresiones algebraicas en forma de factores. Para lograr este objetivo, primero hay que agrupar convenientemente la expresión y observar que cada grupo así formado tenga, en efecto, un factor común.
Aplicar la técnica correctamente requiere algo de práctica, pero en poco tiempo se logra dominar. Veamos primero un ejemplo ilustrativo descrito paso a paso. Luego el lector puede aplicar lo aprendido en cada uno de los ejercicios que aparecerán después.

Por ejemplo supongamos que se necesita factorizar la siguiente expresión:
2x2 + 2xy – 3zx – 3zy
Esta expresión algebraica consta de 4 monomios o términos, separados por signos + y –, a saber:
2x2, 2xy, -3zx, -3zy
Observando con detenimiento, la x es común a los tres primeros, pero no al último, mientras que la y es común al segundo y al cuarto, y la z es común al tercero y al cuarto.
Así que en principio no existe un factor común a los cuatro términos a la vez, pero si se agrupan como se va a mostrar en el apartado siguiente, es posible que sí aparezca uno que ayude a escribir la expresión como el producto de dos o más factores.
Índice del artículo
Factorizar la expresión: 2x2 + 2xy – 3zx – 3zy
Paso 1: Agrupar
2x2 + 2xy – 3zx – 3zy = (2x2 + 2xy) + (-3zx – 3zy)
Paso 2: Sacar el factor común de cada grupo
2x2 + 2xy – 3zx – 3zy =
=(2x2 + 2xy) – (3zx + 3zy) =
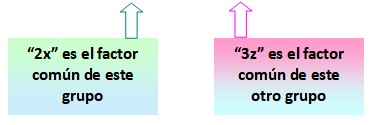
=2x (x+y) – 3z (x+y)
Importante: el signo negativo también es un factor común que debe ser tomado en cuenta.
Ahora nótese que el paréntesis (x+y) está repetido en los dos términos obtenidos al agrupar. Ese es el factor común que se estaba buscando.
Paso 3: Factorizar toda la expresión
2x2 + 2xy – 3zx – 3zy = (x+y) (2x – 3z)
Con el resultado anterior se ha llegado a la meta de la factorización, que no es otra que transformar una expresión algebraica a base de sumas y restas de términos, en el producto de dos o más factores, en nuestro ejemplo, de: (x+y) y (2x – 3z).
Cuestión 1: ¿Cómo saber que el resultado es correcto?
Respuesta: Se aplica la propiedad distributiva al resultado obtenido y después de reducir y simplificar, la expresión así lograda debe coincidir con la original, si no es así, hay un error.
En el ejemplo anterior, se trabaja a la inversa con el resultado, para comprobar que está bien:
(x+y) (2x – 3z) = 2x2 -3zx +2xy – 3zy
Como el orden de los sumandos no altera la suma, luego de aplicar la propiedad distributiva se tienen de regreso todos los términos originales, signos incluidos, por lo tanto, la factorización es correcta.
Cuestión 2: ¿Se podía haber agrupado de otra forma?
Respuesta: Hay expresiones algebraicas que admiten más de una forma de agrupación y otras que no. En el ejemplo seleccionado, el lector puede intentar por su cuenta otras posibilidades, por ejemplo agrupar así:
2x2 + 2xy – 3zx – 3zy = (2x2– 3zx) + (2xy – 3zy)
Y puede comprobar que el resultado es el mismo que se obtuvo aquí. Encontrar la agrupación óptima es cuestión de práctica.
Cuestión 3: ¿Por qué es necesario sacar factor común de una expresión algebraica?
Respuesta: Porque hay aplicaciones en las que la expresión factorizada facilita los cálculos. Por ejemplo, supongamos que se desea hacer 2x2 + 2xy – 3zx – 3zy igual a 0. ¿Cuáles serían las posibilidades?
Para responder esta inquietud, la versión factorizada es mucho más útil que el desarrollo original en términos. Se plantea así:
(x+y) (2x – 3z) = 0
Una posibilidad de que la expresión valga 0 es que x = -y, sin importar el valor de z. Y la otra es que x = (3/2)z, sin que importe el valor de y.
Sacar factor común de la siguiente expresión por agrupación de términos:
ax+ay+bx +by
Solución
Se agrupan los dos primeros, con el factor común “a” y los dos últimos con el factor común “b”:
ax+ay+bx +by = a (x+y) + b (x+y)
Una vez hecho esto se pone de manifiesto un nuevo factor común, que es (x+y), de modo que:
ax+ay+bx +by = a (x+y) + b (x+y) = (x+y)(a+b)
Otra manera de agrupar
Esta expresión admite otra forma de agrupar. Veamos qué sucede si se reordenan los términos y se hace un grupo con los que contienen x y otro con los que contienen y:
ax+ay+bx +by = ax +bx +ay +by = x (a+b) + y (a+b)
De esta manera el nuevo factor común es (a+b):
ax+ay+bx +by = ax +bx +ay +by = x(a+b) + y(a+b) = (x+y)(a+b)
Que conduce al mismo resultado de la primera forma de agrupar que se probó.
Se requiere escribir la siguiente expresión algebraica como el producto de dos factores:
3a3 – 3a2b+9ab2-a2+ab-3b2
Solución
Esta expresión contiene 6 términos. Probemos agrupando primero y cuarto, segundo y tercero y por último quinto y sexto:
3a3 – 3a2b+9ab2-a2+ab-3b2 = (3a3 -a2) + (– 3a2b+9ab2) + (ab-3b2)
Ahora se factoriza cada paréntesis:
= (3a3 -a2) + (– 3a2b+9ab2) + (ab -3b2) = a2 (3a – 1) + 3ab(3b –a ) + b(a-3b)
A primera vista parece que se ha complicado la situación, pero el lector no debe desanimarse, ya que vamos a reescribir el último término:
a2 (3a – 1) + 3ab(3b –a ) + b(a-3b) = a2 (3a – 1) + 3ab (3b-a) – b(3b-a)
Los dos últimos términos tienen ahora un factor común, que es (3b-a), así que se pueden factorizar. Es muy importante no perder de vista el primer término a2 (3a – 1), que debe seguir acompañando todo como sumando, así no se esté trabajando con él:
a2 (3a – 1) + 3ab (3b-a) – b(3b-a) = a2 (3a – 1) + (3b-a)(3ab-b)
La expresión se ha reducido a dos términos y se descubre un nuevo factor común en el último, que es “b”. Ahora queda:
a2 (3a – 1) + (3b-a)(3ab-b) = a2 (3a – 1) +b (3b-a)(3a-1)
El siguiente factor común en aparecer es 3a – 1:
a2 (3a – 1) +b (3b-a)(3a-1) = (3a – 1)[ a2 + b(3b-a)]
O si prefiere sin corchetes:
(3a – 1)[ a2 + b(3b-a)] = (3a – 1)(a2 –ab + 3b2)
¿Puede el lector encontrar otra forma de agrupar que conduzca a este mismo resultado?

- Baldor, A. 1974. Algebra Elemental. Cultural Venezolana S.A.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Principales casos de factorización. Recuperado de: julioprofe.net.
- UNAM. Matemáticas Básicas: Factorización por agrupación de términos. Facultad de Contaduría y Administración.
- Zill, D. 1984. Álgebra y Trigonometría. MacGraw Hill.
