Triángulo obtusángulo: qué es, características, tipos, ejemplos

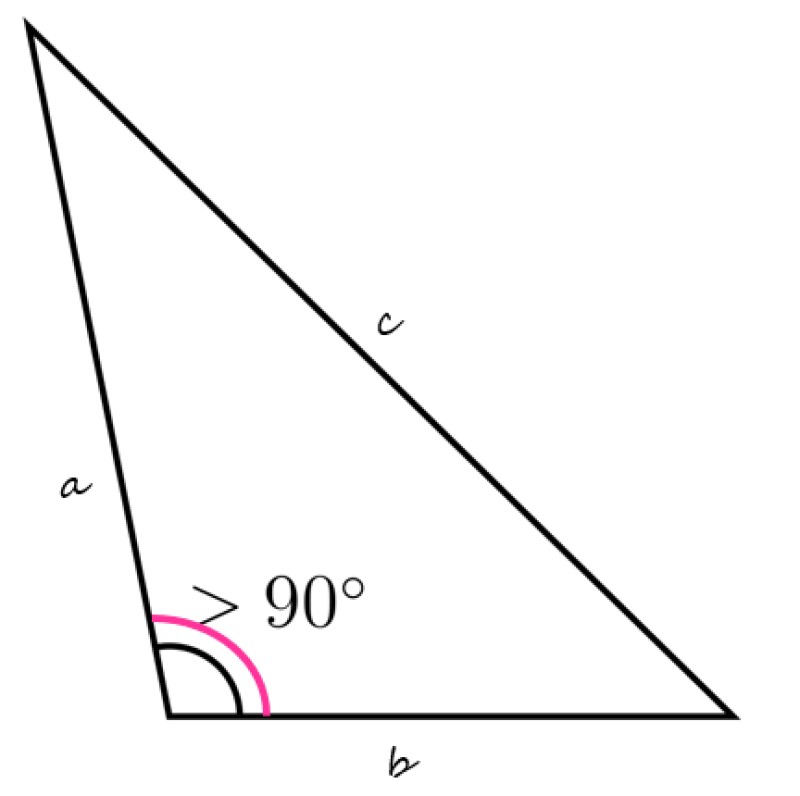
¿Qué es un triángulo obtusángulo?

Un triángulo obtusángulo es la figura plana, cerrada y con tres lados, que además contiene un ángulo interno obtuso, es decir, mayor a 90º y menor de 180º.

Cualquier triángulo contiene 3 ángulos internos, y si uno de ellos es obtuso, los otros dos son, por fuerza, agudos, en virtud de que la suma de los ángulos internos de cualquier triángulo, siempre es igual a 180º.

En la figura de arriba se muestra un ejemplo de triángulo obtusángulo, con el ángulo interno inferior izquierdo mayor a 90º. Los restantes ángulos internos deben sumar menos de 90º, solo así se cumple que la suma de los tres sea igual a 180º.

Además de los triángulos obtusángulos, existen los triángulos acutángulos, si todos sus ángulos internos son agudos, y los triángulos rectángulos, cuando uno de los ángulos internos mide exactamente 90º.

Elementos de los triángulos obtusángulos

Los triángulos obtusángulos poseen los elementos comunes a todos los triángulos: son figuras planas de 3 lados, con 3 ángulos internos y 3 vértices. Además, tienen segmentos notables, llamados cevianas, tales como altura, mediana y mediatriz, y puntos donde las cevianas se intersectan.

Cada uno de estos elementos se define brevemente de la siguiente manera:

-Lados, son los segmentos que conforman la figura.

-Vértices, puntos de intersección de cada pareja de lados adyacentes.

-Ángulos internos, se encuentran entre dos lados adyacentes, por el lado interior de la figura, coincidiendo el vértice del ángulo con el del triángulo.

-Ángulos externos, están entre un lado y la extensión del lado adyacente, por fuera de la figura, siendo común el vértice, tanto del triángulo como del ángulo. La suma de la medida entre el ángulo interno y su ángulo adyacente externo es 180º, de manera que son ángulos complementarios.

-Altura, es la medida del segmento perpendicular que une a un vértice con el lado opuesto, o con la extensión de este.

-Mediana, línea que se dirige desde un vértice hasta el centro del lado opuesto.

-Mediatriz, segmento perpendicular a un lado y que pasa justo por su centro.

-Bisectriz, es un segmento que divide a la mitad un ángulo interno del triángulo.

-Ortocentro, punto de intersección de las tres alturas.

-Baricentro, también llamado centroide, es el punto donde se intersectan las tres medianas.

-Circuncentro, aquí se cortan las tres mediatrices.

-Incentro, punto de confluencia de las bisectrices.

Una vez repasados estos conceptos, algunas de las características más notables de los triángulos obtusángulos se describen a continuación.

Características

1.- La suma de los tres ángulos internos del triángulo obtusángulo es 180º, por ello, solo uno de sus ángulos internos puede ser mayor a 90º, mientras que la suma de los dos restantes es menor a 90º.

2.- El lado más largo del triángulo obtusángulo es opuesto al ángulo obtuso.

3.- En un triángulo obtusángulo, las alturas desde los vértices que hacen ángulo agudo, se cruzan con las extensiones de los lados opuestos.

4.- El ortocentro de un triángulo obtusángulo está fuera de la figura.

5.- El circuncentro del triángulo obtusángulo también cae fuera del triángulo (no sucede así con el triángulo acutángulo).

6.- Solamente es posible inscribir un cuadrado en el triángulo obtusángulo, apoyando uno de los lados del cuadrado sobre el lado más largo del triángulo. Se pueden dibujar dos cuadrados, apoyando el lado sobre los lados más cortos del triángulo, quedando un vértice no inscrito (que no toca el lado del triángulo).

7.- Sea un triángulo obtusángulo de lados (a, b, c), siendo c el lado más largo. La siguiente desigualdad es válida:

a²+b² c²

8.- Sean dos triángulos obtusángulos, cuyos lados respectivos son (a, b, c) y (u, v, w). Los lados más largos de cada uno son c y w, entonces se cumple la siguiente desigualdad:

a∙u + b∙v c∙w

Tipos de triángulos obstusángulos

Los triángulos obtusángulos pueden ser de dos tipos, de acuerdo a la longitud de sus lados:

• Isósceles
• Escaleno

Se describen brevemente a continuación:

Triángulo isósceles

Es aquel que tiene dos lados iguales y uno diferente, es decir, sus lados son (a, a, c).

Cuando el triángulo isósceles es a la vez obtusángulo, los lados de medida “a” son más cortos y el lado “c” es el más largo. El ángulo obtuso se forma entre los lados iguales, mientras que los dos ángulos agudos son de igual medida y se forman entre los lados “a” y el lado “c”.

Y tal como se dijo en la sección precedente, el lado “c”, por ser el más largo, es opuesto al ángulo obtuso.

Triángulo escaleno

Los tres lados del triángulo escaleno tienen distinta medida: (a, b, c).

Ejemplos

Ejemplo 1

El triángulo que se muestra en la siguiente figura es obtusángulo. El ángulo obtuso es γ = 114.5º y se comprueba que la suma de los tres ángulos internos es 180º:

114.5º + 36.8º + 28.6º ≈ 180º

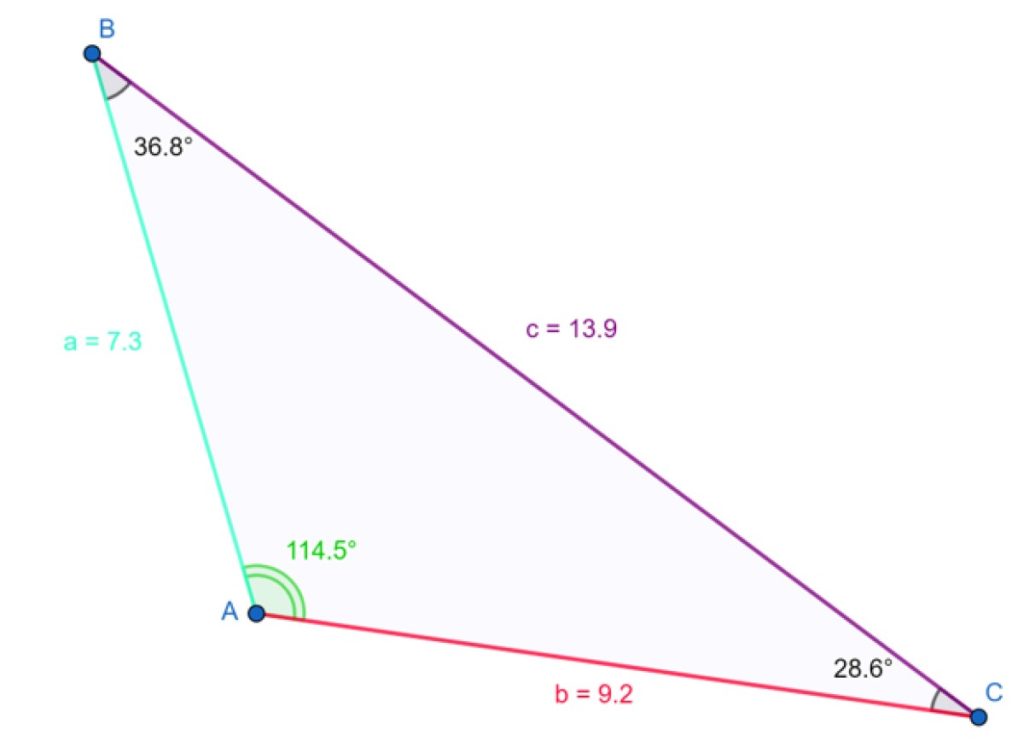
El lado más largo mide 13.9 unidades y es opuesto al ángulo obtuso. También se cumple la desigualdad antes mencionada:

a²+b² c²

Si a = 7.3 y b = 9.2, entonces:

7.3² + 9.2² 13.9²

137.93 193.2

Ejemplo 2

En el triángulo de Calabi, es posible colocar el cuadrado más grande posible, de tres maneras distintas dentro del triángulo, como se muestra en la siguiente figura.

El triángulo de Calabi es isósceles y obtusángulo. El ángulo obtuso mide aproximadamente 101.736° y los ángulos agudos en la base miden ambos 39.13°, también aproximadamente.

Ejercicio resuelto

Los lados iguales de un triángulo isósceles obtusángulo miden 6 cm, mientras que el lado más largo mide 10 cm. Calcular el valor del ángulo obtuso, el de los ángulos águdos restantes y la altura desde dicho vértice hasta la base.

Solución

Se puede emplear el teorema del coseno para encontrar el coseno del ángulo obtuso. Luego, con ayuda de la calculadora se determina el ángulo en cuestión, denotado como γ.

El teorema del coseno afirma que:

c² = a² +b² − 2ab∙cos γ

Donde γ es el ángulo entre los lados a y b. Como el triángulo es isósceles, los lados a y b son iguales, por lo tanto:

c² = 2a² − 2a²∙cos γ

Despejando cos γ:

2α + 112.885º = 180º

α = (180 – 112.885)/2 = 33.558º

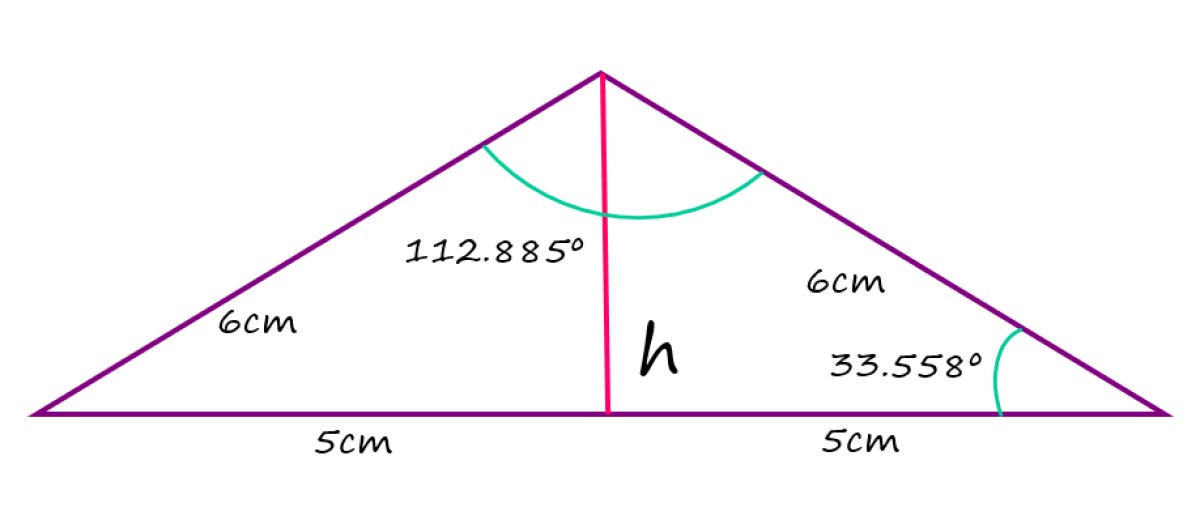
En cuanto a la altura del triángulo, medida desde la base, se obtiene observando que dicha altura divide al triángulo en dos triángulos rectángulos iguales, con hipotenusa igual a 6 cm y base 5 cm. En, tal caso se aplica el teorema de Pitágoras para encontrar directamente el valor de h: