¿Qué es el momento magnético?
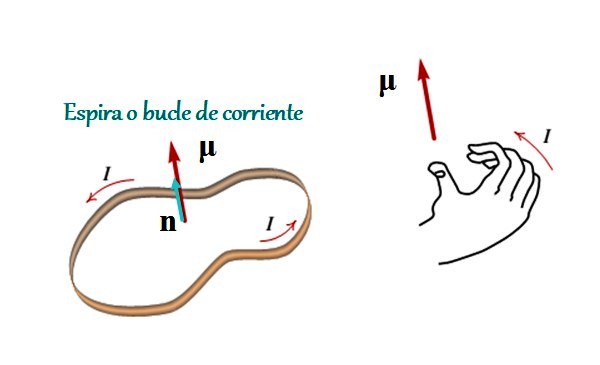
El momento magnético es un vector que relaciona a la corriente que atraviesa una espira o lazo cerrado con el área de la misma. Su módulo es igual al producto de la intensidad de la corriente por el área, y su dirección y sentido vienen dados por la regla de la mano derecha, como se muestra en la figura 1.
Esta definición es válida sin importar la forma de la espira. En cuanto a la unidad del momento magnético, en el Sistema Internacional de unidades SI es Ampere × m2.
En términos matemáticos, denotando al vector momento magnético con la letra griega μ (en negrita porque se trata de un vector y así se distingue de su magnitud), se le expresa como:
μ = IA n
Donde I es la intensidad de la corriente, A es el área que encierra la espira y n es el vector unitario (de módulo igual a 1) que apunta en la dirección perpendicular al plano de la espira, y cuyo sentido está dado por la regla del pulgar derecho (ver la figura 1).
Esta regla es muy simple: enroscando los cuatro dedos de la mano derecha para que sigan a la corriente, el pulgar indica dirección y sentido de n y por consiguiente el del momento magnético.
La ecuación anterior es válida para una espira. Si hay N espiras como en una bobina, el momento magnético se multiplica por N:
μ = NIA n
Índice del artículo
Es sencillo encontrar expresiones para el momento magnético de espiras con formas geométricas regulares:
-Espira cuadrada de lado ℓ: μ = Iℓ2n
–Espira rectangular de lados a y b: μ = Iab n
–Espira circular de radio R: μ = IπR2n
El campo magnético producido por el lazo o espira de corriente se asemeja mucho al de un imán de barra y también al de la Tierra.
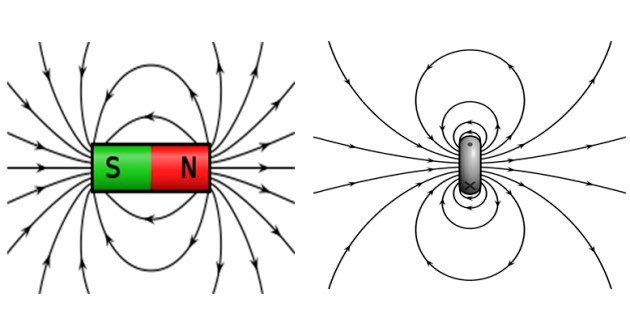
Los imanes de barra se caracterizan por tener polo norte y polo sur, donde los polos opuestos se atraen y los polos iguales se repelen. Las líneas de campo son cerradas, salen del polo norte y llegan al polo sur.
Ahora bien, los polos magnéticos son inseparables, lo cual quiere decir que si se divide un imán de barra en dos imanes más pequeños, estos siguen teniendo sus propios polos norte y sur. No es posible tener los polos magnéticos aislados, por eso es que al imán de barra se lo llama dipolo magnético.
El campo magnético de una espira circular de radio R, que transporta una corriente I, se calcula mediante la ley de Biot-Savart. Para los puntos pertenecientes a su eje de simetría (en este caso el eje x), el campo viene dado por:
Relación entre el campo magnético y el momento magnético del dipolo
Incluyendo el momento magnético en la expresión anterior resulta:
De esta manera, la intensidad del campo magnético es proporcional al momento magnético. Nótese que la intensidad del campo decrece con el cubo de la distancia.
Esta aproximación es aplicable a cualquier espira, siempre y cuando x sea grande en comparación a sus dimensiones.
Y como las líneas de este campo se asemejan tanto a las del imán de barra, la ecuación es un buen modelo para este campo magnético y el de otros sistemas cuyas líneas sean parecidas, como por ejemplo:
-Partículas cargadas en movimiento como el electrón.
-El átomo.
-La Tierra y otros planetas y satélites del Sistema Solar.
-Estrellas.
Una característica muy importante del momento magnético es su vinculación al torque que la espira experimenta en presencia de un campo magnético externo.
Un motor eléctrico contiene bobinas por las que atraviesa una corriente de sentido cambiante y que gracias al campo externo experimentan un efecto de giro. Este giro hace que un eje se mueva y la energía eléctrica se convierta en energía mecánica durante el proceso.
Supongamos, para facilitar los cálculos, una espira rectangular de lados a y b, cuyo vector normal n, saliente a la pantalla, inicialmente es perpendicular a un campo magnético uniforme B, como en la figura 3. Los lados de la espira experimentan fuerzas dadas por:
F = IL x B
Donde L es un vector de magnitud igual a la longitud del segmento y dirigido según la corriente, I es la intensidad de la misma y B es el campo. La fuerza es perpendicular tanto a L como al campo, pero no todos los lados experimentan fuerza.
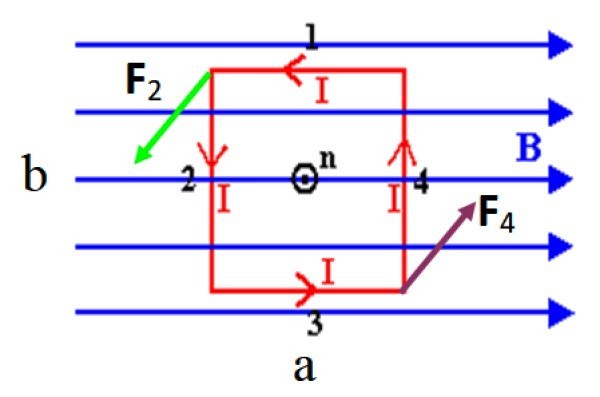
En la figura mostrada, no hay fuerza sobre los lados cortos 1 y 3 por ser paralelos al campo, recuérdese que el producto cruz entre vectores paralelos es nulo. Sin embargo, los lados largos 2 y 4, que son perpendiculares a B, experimentan las fuerzas denotadas como F2 y F4.
Dichas fuerzas forman un par: tienen igual magnitud y dirección, pero sentidos opuestos, por lo tanto no son capaces de trasladar a la espira en medio del campo. Pero pueden hacerla rotar, ya que el torque τ que ejerce cada fuerza, respecto al eje vertical que pasa por el centro de la espira, tiene la misma dirección y sentido.
De acuerdo a la definición de torque, donde r es el vector de posición:
τ = r x F
Entonces:
τ2 = τ4= (a/2) F (+j )
Los torques individuales no se cancelan, ya que tienen la misma dirección y sentido, entonces se suman:
τneto = τ2 + τ4 =a F (+j )
Y siendo la magnitud de la fuerza F = IbB, resulta:
τneto = I⋅a⋅b⋅B (+j )
El producto a⋅b es el área A de la espira, entonces Iab es la magnitud del momento magnético μ. Por lo tanto τneto = μ⋅B (+j )
Se puede ver que, en general, el torque coincide con el producto vectorial entre los vectores μ y B:
τneto = μ x B
Y aunque esta expresión se derivó partiendo de una espira rectangular, es válida para una espira plana de forma arbitraria.
El efecto del campo sobre la espira es un torque que tiende a alinear el momento magnético con el campo.
Para hacer girar a la espira o el dipolo en medio del campo hay que efectuar un trabajo contra la fuerza magnética, el cual cambia la energía potencial del dipolo. La variación de la energía ΔU, cuando la espira rota desde el ángulo θo al ángulo θ viene dada por la integral:
ΔU = -μB cos θ
Que a su vez se puede expresar como el producto escalar entre los vectores B y μ:
ΔU = – μ·B
La energía potencial mínima en el dipolo ocurre cuando cos θ = 1, lo que significa que μ y B son paralelos, la energía es máxima si son opuestos (θ = π) y es nula cuando son perpendiculares (θ = π/2).
- Figueroa, D. 2005. Serie: Física para Ciencias e Ingeniería. Volumen 5. Electromagnetismo. Editado por Douglas Figueroa (USB).
- Resnick, R. 1999. Física. Vol. 2. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 2. Pearson.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 2. 7ma. Ed. Cengage Learning.
- Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 2. Editorial Reverté.
