Aceleración media: cómo se calcula y ejercicios resueltos

La aceleración media a_m es la magnitud que describe la variación de la velocidad de una partícula en el transcurso del tiempo. Es importante, porque pone de manifiesto las variaciones que el movimiento experimenta.

Para expresar esta magnitud en términos matemáticos, es preciso considerar dos velocidades y dos instantes de tiempo, a los que respectivamente se denotan como v₁ y v₂, y t₁ y t₂.

Combinando los valores de acuerdo a la definición ofrecida, se tendrá la siguiente expresión:

En el sistema internacional SI las unidades para a_m serán m/s², aunque otras unidades que involucren longitud por unidad de tiempo al cuadrado servirán.

Por ejemplo está el km/h.s que se lee “kilómetro por hora y por segundo”. Obsérvese que la unidad de tiempo aparece dos veces. Pensando en un móvil que se desplaza a lo largo de una línea recta, significa que por cada segundo transcurrido, el móvil aumenta su rapidez en 1 km/h. O bien la disminuye en 1 km/h por cada segundo que pasa.

Índice del artículo

• 1 Aceleración, velocidad y rapidez
• 2 Cómo se calcula la aceleración media
• 3 Los signos de la aceleración en el movimiento unidimensional
• 4 Caída libre: un movimiento con aceleración constante
• 5 Ejercicio resuelto
  • 5.1 Respuesta
• 6 Referencias

Aceleración, velocidad y rapidez

Aunque se asocia a la aceleración con un incremento de la rapidez, lo cierto es que observando cuidadosamente la definición, resulta que cualquier cambio en la velocidad implica la existencia de una aceleración.

Y la velocidad no siempre cambia necesariamente en magnitud. Puede ocurrir que el móvil solamente varíe de dirección y mantenga constante su celeridad. Aún así hay una aceleración responsable de este cambio.

Ejemplo de ello es un automóvil que da una curva con rapidez constante de 60 km/h. El vehículo está sujeto a una aceleración, la cual se encarga de cambiar la dirección de la velocidad para que el auto siga la curva. El conductor la aplica haciendo uso del volante.

Tal aceleración se dirige hacia el centro de la trayectoria curva, para hacer que el automóvil no se salga de ella. Recibe el nombre de aceleración radial o normal. Si la aceleración radial se anulara súbitamente, el coche ya no podría seguir dando la curva y continuaría en línea recta.

Un auto desplazándose por una curva es un ejemplo de movimiento en dos dimensiones, mientras que cuando marcha en línea recta, su movimiento es unidimensional. En este caso, el único efecto que tiene la aceleración es el de cambiar la rapidez del auto.

A esta aceleración se la denomina aceleración tangencial. No es exclusiva del movimiento unidimensional. El coche que da la curva a 60 km/h podría al mismo tiempo acelerar a 70 km/h mientras la toma. En tal caso el conductor necesita hacer uso tanto del volante como del pedal del acelerador.

Si consideramos un movimiento unidimensional, la aceleración media tiene una interpretación geométrica similar a la de la velocidad media, como pendiente de la recta secante que corta la curva en los puntos P y Q de la gráfica velocidad vs tiempo.

Esto se aprecia en la siguiente figura:

Cómo se calcula la aceleración media

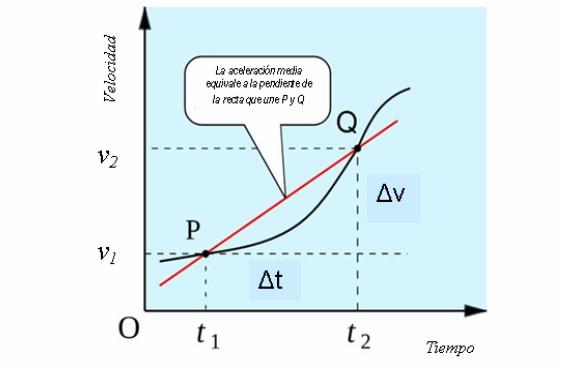
Veamos algunos ejemplos para calcular la aceleración media en diversas situaciones:

I) En un cierto instante de tiempo un móvil que se desplaza a lo largo de una línea recta tiene una velocidad de + 25 km/h y 120 segundos más tarde tiene otra de -10 km/h. ¿Cuál fue la aceleración media?

Respuesta

Como el movimiento es unidimensional se puede prescindir de la notación vectorial, en cuyo caso:

v_o = +25 km/h = +6.94 m/s

v_f = -10 km/h = – 2.78 m/s

Δt = 120 s

Siempre que se tenga un ejercicio con magnitudes mixtas como este, en el cual hay horas y segundos, es necesario pasar todos los valores a las mismas unidades.

Al ser un movimiento unidimensional se ha prescindido de la notación vectorial.

II) Un ciclista se desplaza hacia el este a razón de 2.6 m/s y 5 minutos más tarde va hacia el sur a 1.8 m/s. Encontrar su aceleración media.

Respuesta

El movimiento no es unidimensional, por lo tanto se hace uso de la notación vectorial. Los vectores unitarios i y j indican las direcciones junto a la siguiente convención de signos, facilitando el cálculo:

• Norte: +j
• Sur: –j
• Este: +i
• Oeste: –i

v₂ = – 1.8 j m/s

v₁ = + 2.6 i m/s

Δt = 5 minutos = 300 segundos

Los signos de la aceleración en el movimiento unidimensional

Como siempre que sucede con las magnitudes medias o promedio, la información brindada es global. No ofrecen detalles de lo sucedido con el móvil en cada instante de tiempo, sin embargo lo que aportan sigue siendo valioso para la descripción del movimiento.

Mediante los signos tanto de la velocidad como de la aceleración, es posible saber si un móvil que se desplaza sobre una recta acelera o frena. En ambas situaciones la aceleración está presente, ya que la velocidad está cambiando.

Estas son algunas consideraciones interesantes en cuanto a los signos de estas dos magnitudes:

• Velocidad y aceleración media, ambas del mismo signo, significa que visto globalmente, el móvil va cada vez más deprisa.
• Velocidad y aceleración con signos diferentes es señal de un móvil ha estado más bien frenando.

Suele pensarse que siempre que se trate de una aceleración negativa el móvil está frenando. Esto es cierto si la velocidad del móvil es positiva. Pero si es negativa, en realidad la celeridad va en aumento.

Como siempre cuando se estudio el movimiento, se piensa en los casos especiales. Por ejemplo ¿qué sucede cuando la aceleración media es nula?. ¿Significa que el móvil ha mantenido siempre su velocidad constante?

La respuesta es no. El móvil pudo haber variado su velocidad en el intervalo considerado, pero la velocidad inicial y la final fueron las mismas. Por el momento se desconoce el detalle de lo sucedido en el intervalo, ya que la aceleración media no ofrece más información.

¿Y si la aceleración media a_m es igual a la aceleración a en cualquier punto del intervalo temporal? Esta es una situación muy interesante llamada Movimiento Rectilíneo Uniformemente Variado o MRUV por sus siglas.

Significa que la velocidad cambia de manera uniforme a lo largo del tiempo. Por lo tanto la aceleración es constante. En la naturaleza existe un movimiento así, con el cual todos están familiarizados: la caída libre.

Caída libre: un movimiento con aceleración constante

Es un hecho conocido que la tierra atrae a los objetos hacia su centro y que al liberar alguno a cierta altura, este experimenta la aceleración de la gravedad, cuyo valor es aproximadamente constante e igual 9.8 m/s² cerca de la superficie.

Si la resistencia del aire no interviene, el movimiento es vertical y se conoce como caída libre. Cuando la aceleración es constante y escogiendo t₀ = 0, la ecuación de la aceleración media se transforma en:

v_f = v₀ + at = gt (v₀= 0)

Donde a = g = 9.8 m/s²

Ejercicio resuelto

Se deja caer un objeto desde suficiente altura. Encontrar la velocidad al cabo de 1.25 segundo.

Respuesta

v_o = 0, ya que el objeto se deja caer, entonces:

v_f = gt = 9.8 x 1.25 m/s = 12.25 m/s, dirigida verticalmente hacia el suelo. (Se ha tomado la dirección vertical hacia abajo como positiva).

A medida que el objeto se aproxima al suelo, su velocidad aumenta en 9.8 m/s por cada segundo transcurrido. La masa del objeto no está involucrada. Dos objetos diferentes, dejados caer desde la misma altura y al mismo tiempo, desarrollan la misma velocidad a medida que caen.

Referencias

1. Giancoli, D. Physics. Principles with Applications. Sixth Edition. Prentice Hall. 21- 35.
2. Resnick, R. (1999). Física. Volumen 1. Tercera edición en español. México. Compañía Editorial Continental S.A. de C.V. 20-34.
3. Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7^ma. Edición. México. Cengage Learning Editores. 21-39.