Conservación del momento lineal: principio, ejemplos, ejercicios.
La conservación del momento lineal de un cuerpo establece que el producto de su masa por su vector velocidad es una cantidad constante, cuando el cuerpo está libre de interacción con otros cuerpos y con la velocidad medida respecto a un sistema de referencia fijo o no-acelerado.
Cuando se tienen varios cuerpos que interactúan solo entre ellos, pero no con el medio exterior, entonces el momento lineal del conjunto también permanece constante a través del tiempo.

El momento lineal, cantidad de movimiento lineal o simplemente el momentum, se denota con la letra p y es una cantidad vectorial:

El momento lineal no es lo mismo que la velocidad, aunque la relación es evidente: por ejemplo, un camión que va a 20 km/h tiene más momento lineal que una bicicleta que se mueva a la misma velocidad.
Para que el momento lineal de un cuerpo cambie, es necesario que sobre él esté actuando una fuerza externa neta, de lo contrario permanece constante. Además, el momento lineal P de un sistema formado por n-cuerpos es la suma vectorial de los momentos individuales:
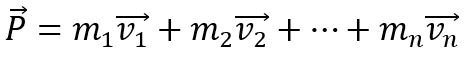
Índice del artículo
- 1 Principio de la conservación de la cantidad de movimiento lineal
- 2 Ejemplos
- 3 Aplicaciones
- 4 Ejercicios
- 5 Referencias
En un cuerpo libre de fuerzas (o bien uno en el que todas las fuerzas sobre el mismo se cancelen) ocurre que el momento lineal se mantiene constante.
De igual manera pasa en un sistema formado por varios cuerpos que solo interactúan entre sí, pero no con el medio exterior: el momento lineal total del sistema permanece fijo durante la evolución del movimiento del conjunto.
Este principio de conservación se enuncia así:
El momento lineal total de un conjunto de n-cuerpos que solo interactúan entre sí, pero no con el medio exterior, es una cantidad invariable en el tiempo.
Y matemáticamente se expresa de la siguiente manera:

Las igualdades anteriores se cumplen, si y solo si los n-cuerpos interactúan entre ellos, pero no con el medio exterior. Además, los momentos individuales siempre deben medirse respecto de un sistema de referencia inercial.

Dos astronautas en el espacio están tomados de las manos y se mantienen en una posición fija respecto de la nave. Pero sí se empujan uno al otro, comienzan a separarse en direcciones contrarias, cuando son vistos desde la nave.
En este caso, como la interacción entre los astronautas es solo entre ellos a través de la fuerza de contacto de sus manos, el momento lineal total después de empujarse sigue siendo el valor inicial respecto de la nave. Es decir, momento lineal total 0.
Sin embargo, el momento lineal de cada astronauta sí que cambió. Inicialmente cada uno tenía momento lineal 0 respecto de la nave, pero después de empujarse uno sale en una dirección y el otro en la dirección contraria, con momentos lineales no-nulos de igual magnitud y direcciones contrarias.
Así, cuando los momentos individuales se suman vectorialmente, se obtiene como resultado el momento lineal total inicial, que es nulo.
Por otra parte, la conservación de la cantidad momento lineal señala que el astronauta con menor masa es el que se mueve con mayor rapidez respecto de la nave. Pero el resultado de multiplicar su masa por su rapidez, es igual al producto obtenido al multiplicar la masa del otro por la rapidez del otro.
Un perrito está sobre una plataforma flotante en un lago de aguas tranquilas y su dueño lo ve desde un muelle. Al comienzo, tanto la plataforma como el perrito están en reposo, pero cuando el perrito quiere acercarse al dueño, la plataforma se aleja del muelle.
La explicación a esta observación está justamente en el principio de conservación de la cantidad de momento lineal. El sistema está constituido por el perrito y la plataforma.
El perrito puede caminar sobre la plataforma gracias a la fuerza de fricción entre sus patas y la superficie, en este caso la fuerza de fricción es una fuerza interna de interacción entre él y la plataforma.
El conjunto es un sistema aislado, ya la plataforma puede moverse horizontalmente sobre el lago, libre de toda resistencia al movimiento. Por otra parte, en la dirección vertical todas las fuerzas se equilibran y se compensan, y el conjunto no tiene movimiento en esa dirección.
Por lo tanto, en esta situación se cumplen todas las hipótesis para que el principio de conservación del momento lineal se aplique.

Un esquimal queda atrapado en el centro de un lago helado, el hielo es tan liso que por más que lo intenta, el esquimal resbala y siempre queda en el mismo lugar.
La única forma posible de que el esquimal salga del lago, es que lance en la dirección contraria a la que desea moverse algún objeto pesado que lleve en su mochila (suponiendo que lleve uno).

La conservación del momento lineal se aplica para impulsar un cohete en el espacio exterior donde no hay fuerzas externas. En este caso el impulso de la nave se logra mediante la expulsión de gases a gran velocidad, para que el cohete pueda moverse en la dirección contraria a la que fueron expulsados.
Si originalmente la nave está en reposo, cuando se quema y expulsa combustible, la fuerza de la expulsión ocurre contra la propia nave. Se trata de una fuerza interna entre los gases y la nave. No hay fuerzas exteriores y por tanto aplica la conservación del momento lineal.
Como el momento lineal de los gases es igual y contrario al de la nave, esta logra salir del reposo, y al seguir expulsando gases, incrementa su cantidad de movimiento y por tanto su velocidad.

Otro caso de aplicación de la conservación del momento lineal en la vida cotidiana es incrustar un clavo en la madera aprovechando la cantidad de movimiento o momento lineal del martillo.
Se podría argumentar que en este caso el principio no aplica, porque sí hay una fuerza externa: la resistencia que ofrece la madera al clavo.
Sin embargo, en el momento del contacto, la fuerza que el martillo imprime al clavo es una fuerza interna (entre el sistema que es el clavo y el martillo) mucho más grande que la resistencia que opone la madera, y por tanto esta última es despreciable.
Todo el momento lineal del martillo, que es bastante grande debido a su gran masa y velocidad, se transfiere al clavo justo después de la colisión. Nótese que se transfiere todo el momento, pero no toda la energía cinética del martillo, ya que parte de esta se transforma en energía térmica en el clavo y en el martillo, que elevan su temperatura después del impacto.
Los astronautas Andrew y Berenice están fuera de la estación espacial tomados de las dos manos y en reposo respecto a la estación. Se impulsan empujando las manos de uno contra las del otro y se sueltan. Si Andrew, de 70 kg de masa se mueve a 1 m/s respecto de la estación ¿cuál es la rapidez de Berenice con 49 kg de masa?
Solución
En este caso claramente se aplican las hipótesis de la conservación del momento lineal, ya que en el espacio exterior no hay fuerzas externas. La fuerza con la que empujan sus manos ambos astronautas es una fuerza interna.
Supongamos que la masa de Andrew es Ma y la de Berenice Mb. Similarmente, las velocidades de ambos de después del impulso son Va para Andrew y Vb para Berenice. Entonces la conservación del momento lineal se aplica así:
Ma∙0 + Mb∙0 = Ma∙Va+ Mb∙Vb
Despejando la velocidad de Berenice se tiene:
Vb = – (Ma / Mb) ∙ Va
Colocando los valores numéricos:
Vb = – (70 / 49) ∙ (1m/s) û = -1,43m/s û
Es decir que Berenice se mueve con rapidez de 1,43 m/s en dirección contraria a la de Andrew.

Un perrito de 5 kg de masa está en reposo sobre una plataforma de 15 kg que flota, también en reposo, sobre un lago quieto. Si el perrito comienza a caminar sobre la plataforma a razón de 0,5 m/s respecto de esta. ¿Qué rapidez tendrá el perrito y la plataforma respecto de un observador fijo a tierra?
Solución
Se tomará como sistema inercial de referencia al muelle donde se encuentra el dueño del perrito. Inicialmente tanto el cachorro como la plataforma flotante se encuentran en reposo respecto del muelle.
Cuando el perrito decide caminar hacia el dueño con rapidez v’ respecto de la plataforma, entonces la plataforma se aleja del muelle con velocidad +V. La velocidad del perrito respecto del muelle se consigue mediante la suma vectorial de su velocidad respecto de la plataforma más la velocidad de la plataforma y la denotamos por:
v = –v’ + V
Como la resistencia del agua al movimiento de la plataforma es prácticamente nula debido a su baja rapidez, entonces puede afirmarse que el sistema conformado por el perrito + la plataforma es un sistema aislado y se aplica el principio de conservación del momento lineal:
0 = m∙v + M∙V
Recordando que v = v’ + V se tiene:
0 = -m∙v’ + m∙v + M∙V
Es decir: m∙v’ = (m+M)∙V
Por lo tanto V = [m/(m +M)] v’ y v = -(M/m) V = – [M/(m + M)] v’
Sustituyendo los valores numéricos se tiene:
V = [5 /(5 +15)]∙0,5m/s = 0,125 m/s
Esta es la velocidad con la que se aleja la plataforma del muelle.
V = -(15/20) ∙0,5m/s = -0,375 m/s
Y esta es la velocidad con la que el perrito se acerca al muelle.
- Duke University. Systems of Particles. Recuperado de: webhome.phy.duke.edu.
- Rex, A. 2011. Fundamentos de Física. Pearson.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Tipler, P. (2006). Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté.
