Matriz ortogonal: propiedades, demostración, ejemplos
Se tiene una matriz ortogonal cuando dicha matriz multiplicada por su transpuesta da como resultado la matriz identidad. Si la inversa de una matriz es igual a la transpuesta entonces la matriz original es ortogonal.
Las matrices ortogonales tienen como característica que el número de filas es igual al número de columnas. Además, los vectores fila son vectores ortogonales unitarios y los vectores fila de la transpuesta también lo son.
Cuando una matriz ortogonal se multiplica por los vectores de un espacio vectorial produce una transformación isométrica, es decir, una transformación que no cambia las distancias y preserva los ángulos.
Un representante típico de las matrices ortogonales son las matrices de rotación. Las transformaciones de las matrices ortogonales sobre un espacio vectorial se denominan transformaciones ortogonales.
Las transformaciones geométricas de rotación y reflexión de puntos representados por sus vectores cartesianos, se efectúa mediante la aplicación de matrices ortogonales sobre los vectores originales para obtener las coordenadas de los vectores transformados. Es por esta razón que las matrices ortogonales son ampliamente usadas en el procesamiento gráfico computacional.
Índice del artículo
Una matriz M es ortogonal si multiplicada por su transpuesta MT da como resultado la matriz identidad I. De igual forma, el producto de la transpuesta de una matriz ortogonal por la matriz original de como resultado la matriz identidad:
M MT = MT M = I
Como consecuencia de la afirmación anterior, se tiene que la transpuesta de una matriz ortogonal es igual a su matriz inversa:
MT = M-1.
El conjunto de las matrices ortogonales de dimensión n x n forman el grupo de ortogonal O(n). Y el subconjunto de O(n) de matrices ortogonales con determinante +1 forman el Grupo de Matrices Especiales Unitarias SU(n). Las matrices del grupo SU(n) son matrices que producen transformaciones lineales de rotación, también conocidas como el grupo de rotaciones.
Quremos demostrar que una matriz es ortogonal si, y solo si, los vectores fila (o los vectores columna) son ortogonales entre sí y de norma 1.
Suponga que las filas de una matriz ortogonal n x n son n vectores ortonormales de dimensión n. Si se denota por v1, v2, …., vn a los n vectores se cumple:
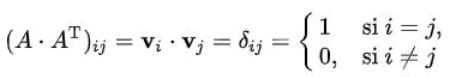
Donde queda evidente que efectivamente el conjunto de vectores fila es un conjunto de vectores ortogonales con norma uno.
Demuestre que la matriz 2 x 2 que en su primera fila tiene el vector v1= (-1 0) y en su segunda fila el vector v2= (0 1) es una matriz ortogonal.
Solución: Se construye la matriz M y se calcula su transpuesta MT:
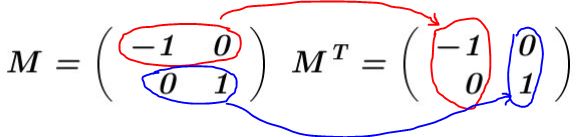
En este ejemplo, la matriz M es auto transpuesta, es decir que la matriz y su transpuesta son idénticas. Se multiplica M por su transpuesta MT:
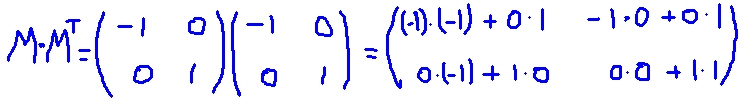
Se verifica que MMT es igual a la matriz identidad:
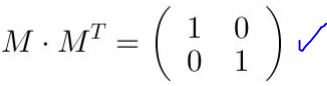
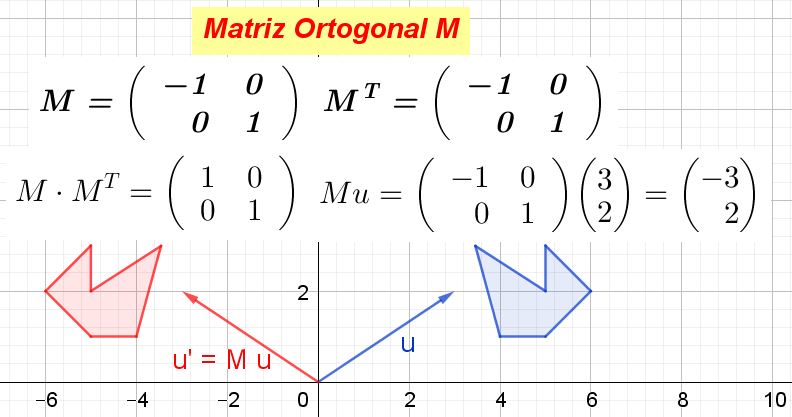
Cuando la matriz M se multiplica por las coordenadas de un vector o de un punto, se obtienen unas nuevas coordenadas que corresponden a la transformación que la matriz hace sobre el vector o el punto.
En la figura 1 se muestra como M transforma el vector u en u’y también como M transforma el polígono azul en el polígono rojo. Como M es ortogonal se trata entonces de una transformación ortogonal, la cual preserva las distancias y los ángulos.
Suponga que tiene una matriz 2 x 2 definida en los reales dada por la siguiente expresión:
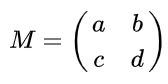
Encontrar los valores reales de a, b, c y d de modo tal que la matriz M sea una matriz ortogonal.
Solución: Por definición, una matriz es ortogonal si multiplicada por su transpuesta se obtiene como resultado la matriz identidad. Recordando que la matriz transpuesta se obtiene de la original, intercambiando filas por columnas se tiene la siguiente igualdad:
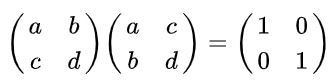
Realizando la multiplicación matricial se tiene:
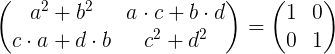
Igualando los elementos de la matriz izquierda con los elementos de la matriz identidad en la derecha, obtenemos un sistema de cuatro ecuaciones con cuatro incógnitas a, b, c y d.
Proponemos para a, b, c y d las siguientes expresiones en función de razones trigonométricas seno y coseno:
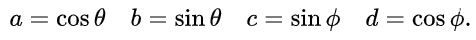
Con esta propuesta y debido a la identidad trigonométrica fundamental se satisface automáticamente la primera y tercera ecuación en la igualdad de los elementos matriciales. La tercera y la cuarta ecuación son la misma y en la igualdad matricial después de sustituir por los valores propuestos queda así:
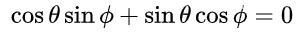
lo que conduce a la siguiente solución:
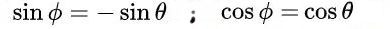
Finalmente se obtienen las siguientes soluciones para para la matriz ortogonal M:
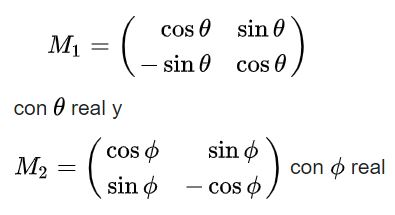
Note que la primera de las soluciones tiene determinante +1 por lo que pertenece al grupo SU(2), mientras la segunda solución tiene determinante -1 y por tanto no pertenece a este grupo.
Dada la siguiente matriz, encuentre los valores de a y de b para que se tenga una matriz ortogonal.
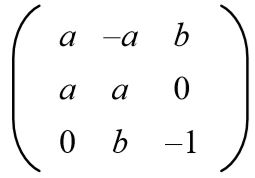
Solución: Para que una matriz dada sea ortogonal, el producto con su transpuesta debe ser la matriz identidad. Entonces, se efectúa el producto matricial de la matriz dada con su matriz transpuesta dando el siguiente resultado:
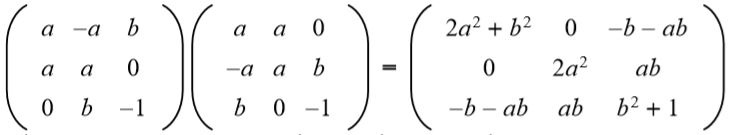
A continuación, se iguala el resultado con la matriz identidad 3 x 3:
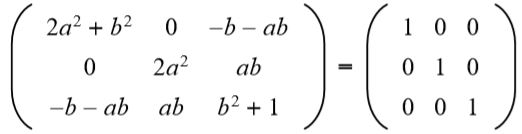
En la segunda fila tercera columna se tiene (a b = 0), pero a no puede ser cero, porque de ser así no se cumpliría la igualdad de los elementos de la segunda fila y segunda columna. Entonces necesariamente b = 0. Sustituyendo b por el valor 0 nos queda:
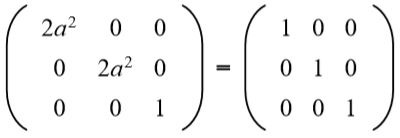
Luego se resuelve la ecuación: 2a^2 = 1, cuyas soluciones son: +½√2 y -½√2.
Tomando la solución positiva para a se tiene como resultado la siguiente matriz ortogonal:
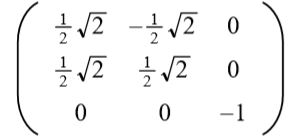
El lector puede verificar fácilmente que los vectores filas ( y también los vectores columnas) son ortogonales y unitarios, es decir ortonormales.
Demostrar que la matriz A cuyos vectores filas son v1= (0, -1 0), v2= (1, 0, 0) y v3= (0 0 -1) es una matriz ortogonal. Adicionalmente encuentre como se transforman los vectores de la base canónica i, j , k a los vectores u1, u2 y u3.
Solución: Debe recordarse que el elemento (i,j) de una matriz multiplicada por su transpuesta, es el producto escalar del vector de la fila (i) por el de la columna (j) de la transpuesta. Además este producto es igual a la delta de Kronecker en caso que la matriz sea ortogonal:
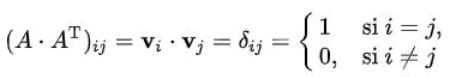
En nuestro caso queda así:
v1 • v1 = 0x0 + (-1)x(-1) + 0x0 = 1
v2 • v2 = 1×1 + 0x0 + 0x0 = 1
v3 • v3 = 0x0 + 0x0 + (-1)x(-1) = 1
v1 • v2 = 0x1 + (-1)x0 + 0x0 = 0
v2 • v1 = 1×0 + 0x(-1) + 0x0 = 0
v2 • v3 = 1×0 + 0x(0) + 0x(-1) = 0
v3 • v2 = 0x1 + 0x(0) + (-1)x0 = 0
v1 • v3 = 0x0 + (-1)x(0) + 0x(-1) = 0
v3 • v1 = 0x0 + 0x(-1) + (-1)x0 = 0
Con lo que queda demostrado que se trata de una matriz ortogonal.
Además u1 = A i = (0, 1, 0); u2 = A j = (-1, 0, 0) y por último u3 = A k = (0, 0, -1)
- Anthony Nicolaides (1994) Determinants & Matrices. Pass Publication.
- Birkhoff and MacLane. (1980). Álgebra moderna, ed. Vicens-Vives, Madrid.
- Casteleiro Villalba M. (2004) Introducción al álgebra lineal. ESIC Editorial.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: A Student’s Survival Guide. Cambridge University Press.
- Richard J. Brown (2012) 30-Second Maths: The 50 Most Mind-Expanding Theories in Mathematics. Ivy Press Limited.
- Wikipedia. Matriz ortogonal. Recuperado de: es.wikipedia.com
- Wikipedia. Orthogonal matrix. Recuperado de: en.wikipedia.com
