Números trascendentes: cuáles son, fórmulas, ejemplos, ejercicios
Los números trascendentes son aquellos que no pueden obtenerse como resultado de una ecuación polinómica. Lo contrario a un número trascendente es un número algebraico, que son soluciones de una ecuación polinómica del tipo:
an xn + an-1 xn-1 + ……+ a2 x2 + a1 x + a0 = 0
Donde los coeficientes an, an-1, ….. a2, a1, a0 son números racionales, llamados los coeficientes del polinomio. Si un número x es solución de la ecuación anterior, entonces ese número no es trascendente.

Analizaremos unos cuantos números y veremos si son o no trascendentes:
a) 3 no es trascendente porque es solución de x – 3 = 0.
b) -2 no puede ser trascendente porque es solución de x + 2 =0.
c) ⅓ es solución de 3x – 1 = 0
d) Una solución de la ecuación x2 – 2x + 1 = 0 es √2 -1, por lo que dicho número por definición no es trascendente.
e) Tampoco lo es √2 porque es el resultado de la ecuación x2 – 2 = 0. Al elevar √2 al cuadrado da como resultado 2, que restado de 2 da igual a cero. Entonces √2 es un número irracional pero no es trascendente.
Índice del artículo
- 1 ¿Cuáles son números trascendentes?
- 2 Fórmulas donde aparece el número trascendente π
- 3 Ejercicios
- 4 Referencias
El problema es que no hay una regla general para obtenerlos (más adelante diremos una forma), pero algunos de los más famosos son el número pi y el número de Neper, denotados respectivamente por: π y e.
El número π aparece naturalmente observando que el cociente matemático entre el perímetro P de un círculo y su diámetro D, independientemente de si se trata de un círculo pequeño o grande, siempre da el mismo número, llamado pi:
π = P/D ≈ 3,14159……
Esto significa que si se toma como unidad de medida el diámetro de la circunferencia, para todas ellas, sean grandes o pequeñas, el perímetro valdrá siempre P = 3,14…= π, tal como puede verse en la animación de la figura 2.
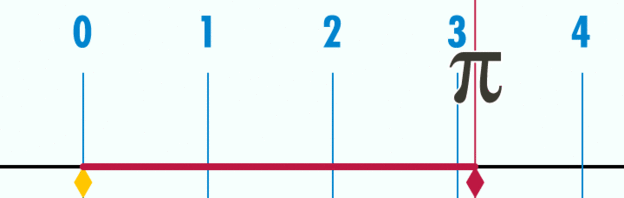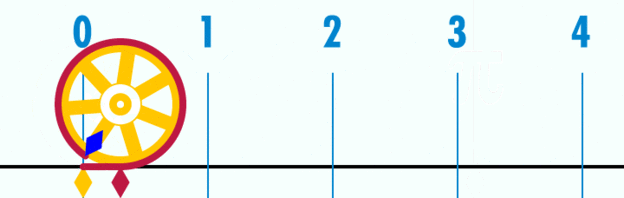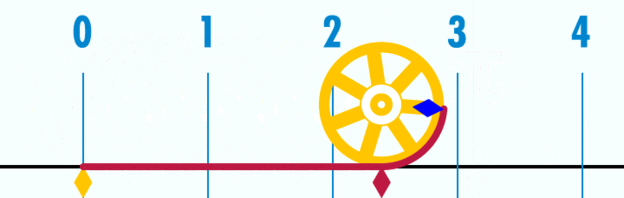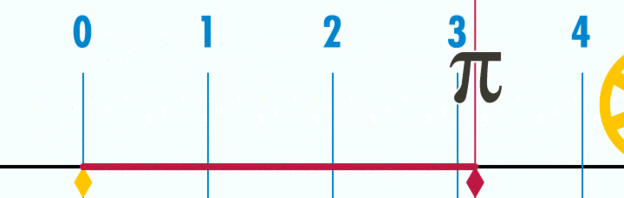
Para poder determinar más decimales hay que medir con mayor precisión P y D y luego calcular el cociente, lo cual se ha hecho en forma matemática. La conclusión es que los decimales del cociente no tienen fin y nunca se repiten, por lo que el número π además de ser trascendente también es irracional.
Un número irracional es aquel número que no puede ser expresado como la división de dos números enteros.
Se sabe que todo número trascendente es irracional, pero no es cierto que todos los irracionales sean trascendentes. Por ejemplo √2 es irracional, pero no es trascendente.

El número trascendente e es la base de los logaritmos neperianos y su aproximación decimal es:
e ≈ 2.718281828459045235360….
Si se quisiera escribir el número e en forma exacta, sería necesario escribir infinitos decimales, porque todo número trascendente es irracional, tal como se dijo antes.
Los primeros diez dígitos de e son fáciles de recordar:
2,7 1828 1828 y aunque pareciera seguir un patrón repetitivo, este no se consigue en los decimales de orden mayor a nueve.
Una definición más formal de e es la siguiente:
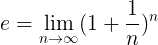
Lo que significa que el valor exacto de e se consigue realizando la operación indicada en esta fórmula, cuando el número natural n tiende a infinito.
Esto explica por qué solo podemos obtener aproximaciones de e, ya que por más grande que se coloque el número n, siempre se podrá encontrar un n mayor.
Busquemos por cuenta propia algunas aproximaciones:
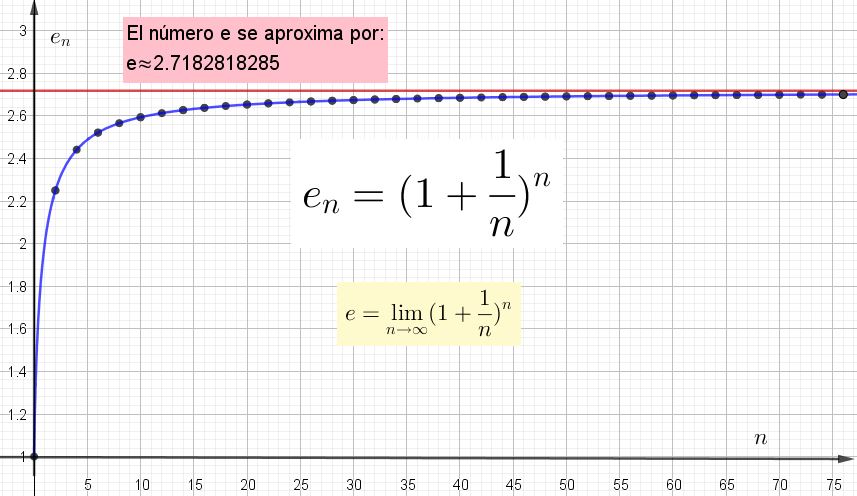
-Cuando n = 100 entonces (1 + 1/100)100 = 2,70481 que apenas coincide en el primer decimal con el “verdadero” valor de e.
-Si se elige n = 10.000 se tiene (1 + 1/10.000)10.000 = 2,71815 que coincide con el valor “exacto” de e en los tres primeros decimales.
Habría que seguir este proceso al infinito para poder obtener el “verdadero” valor de e. No creo que tengamos tiempo de lograrlo, pero hagamos un intento más:
Usemos n=100.000:
(1 + 1/100.000)100.000 = 2,7182682372
Que solo tiene cuatro decimales coincidentes con el valor considerado exacto.
Lo importante es entender que entre mayor sea el valor de n elegido para calcular en, más cerca se estará del valor verdadero. Pero ese valor verdadero solo se tendrá cuando n sea infinito.
Otros números trascendentes
Aparte de estos números famosos hay otros números trascendentes, por ejemplo:
– 2√2
Todo número algebraico, que no sea 0 o 1, elevado a un exponente irracional será un número trascendente.
-El número de Champernowne en base 10:
C_10 = 0,123456789101112131415161718192021….
-El número de Champernowne en base 2:
C_2 = 0,1101110010110111….
-El número Gamma γ o constante de Euler-Mascheroni:
γ ≈ 0,577 215 664 901 532 860 606
Que se obtiene haciendo el siguiente cálculo:
γ ≈ 1 + ½ + ⅓ + ¼ + … + 1/n – ln(n)
Para cuando n sea muy muy grande. Para tener el valor exacto del número Gamma se necesitaría hacer el cálculo con n infinito. Algo parecido a lo que hicimos más arriba.
Y hay muchos números trascendentes más. El gran matemático Georg Cantor, nacido en Rusia y que vivió entre 1845 y 1918, demostró que el conjunto de los números trascendentes es mucho mayor que el conjunto de los números algebraicos.
P = π D = 2 π R, donde P es el perímetro, D el diámetro y R el radio de la circunferencia. Debe recordarse que:
-El diámetro de la circunferencia es el segmento más largo que une dos puntos de la misma y que siempre pasa por su centro,
-El radio es la mitad del diámetro y es el segmento que va del centro al borde.
A = π R2 = ¼ π D2
S= 4 π R2.
Sí. Aunque no lo parezca, la superficie de una esfera es la misma que la de cuatro círculos del mismo radio que la esfera.
V= 4/3 π R3
La pizzería “EXÓTICA” vende pizzas de tres diámetros: pequeña de 30 cm, mediana de 37 cm y grande de 45 cm. Un niño tiene mucha hambre y se dio cuenta que dos pizzas pequeñas tienen el mismo costo que una grande. ¿Qué será mejor para él, comprar dos pizzas pequeñas o una grande?

Solución
Entre mayor sea el área mayor será la cantidad de pizza, por esta razón se calculará el área de una pizza grande y se comparará con la de dos pizzas pequeñas:
Área de la pizza grande = ¼ π D2 = ¼ ⋅3,1416⋅452 = 1590,44 cm2
Área de la pizza pequeña = ¼ π d2 = ¼ ⋅3,1416⋅302 = 706,86 cm2
Por lo tanto dos pizzas pequeña tendrán un área de
2 x 706,86= 1413,72 cm2 .
Queda claro: se tendrá mayor cantidad de pizza comprando una sola grande que dos pequeñas.
La pizzería “EXÓTICA” vende también una pizza semiesférica de 30 cm de radio por el mismo precio de una de forma rectangular de 30 x 40 cm de lado. ¿Cuál elegirías tú?

Solución
Como se ha dicho en la sección anterior, la superficie de una esfera es cuatro veces mayor que la de un círculo del mismo diámetro, por lo que una semiesfera de 30 cm de diámetro tendrá:
Pizza semiesférica de 30 cm: 1413,72 cm2 (el doble de una circular del mismo diámetro)
Pizza rectangular: (30 cm)x(40 cm) = 1200 cm2 .
La pizza semiesférica tiene mayor área.
- Fernández J. El número e. Origen y curiosidades. Recuperado de: soymatematicas.com
- Disfruta las matemáticas. El número de Euler. Recuperado de: disfrutalasmatematicas.com.
- Figuera, J. 2000. Matemática 1ro. Diversificado. ediciones CO-BO.
- García, M. El número e en el cálculo elemental. Recuperado de: matematica.ciens.ucv.ve.
- Wikipedia. Número pi. Recuperado de: wikipedia.com
- Wikipedia. Números trascendentes. Recuperado de: wikipedia.com
