¿Qué relación hay entre el área del rombo y la del rectángulo?

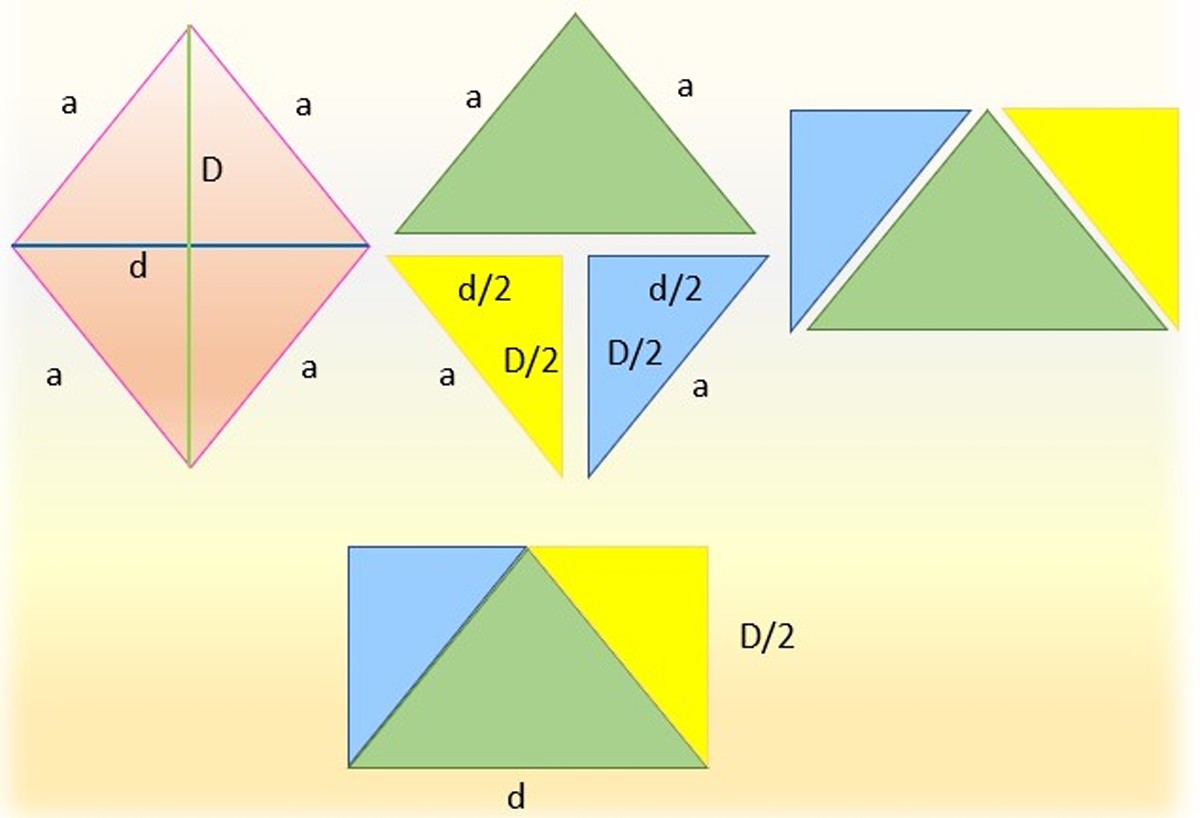
Es posible calcular el área del rombo (y algunas otras figuras geométricas) a partir del área de un triángulo o un cuadrilátero relacionado, tal como un paralelogramo o bien un rectángulo.

El área del rectángulo y la del paralelogramo es la misma: se calcula como el producto entre la base de la figura y su altura con respecto a esa base. Por su parte, el área del triángulo es el semiproducto entre su base y su altura.

Estas fórmulas son fáciles de recordar aunque, naturalmente, la geometría ofrece una fórmula exclusiva para el área del rombo, conociendo la medida de sus diagonales mayor y menor, denotadas como D y d, respectivamente:

Para ello se corta el rombo de la izquierda por una de sus diagonales, lo cual se hizo en la figura seccionando por la diagonal menor, obteniendo así dos triángulos. Se deja el triángulo superior (en verde) y el inferior se divide a su vez en dos triángulos, cortando por la mitad de la diagonal mayor, obteniéndose los triángulos rectángulos idénticos azul y amarillo.

Seguidamente las hipotenusas de estos triángulos se hacen coincidir con los lados del triángulo verde, ya que miden lo mismo, es decir “a”. Y se obtiene finalmente un rectángulo, cuya base es la diagonal menor “d” y cuya altura es la mitad de la diagonal mayor, es decir: “D/2”.

El área del rectángulo así formado coincide exactamente con la del rombo, por lo tanto se puede afirmar que:

A _rombo = (base × altura) _rectángulo = d×(D/2)

Un resultado que, como se puede ver, coincide exactamente con la fórmula del área del rombo dada antes.

Área del rombo y del paralelogramo

El área del rombo también se relaciona con la de un paralelogramo, ya que ambas figuras geométricas son planas y pertenecen a la familia de los cuadriláteros. Por ejemplo, en la siguiente imagen hay un rombo a la izquierda y un paralelogramo a la derecha.

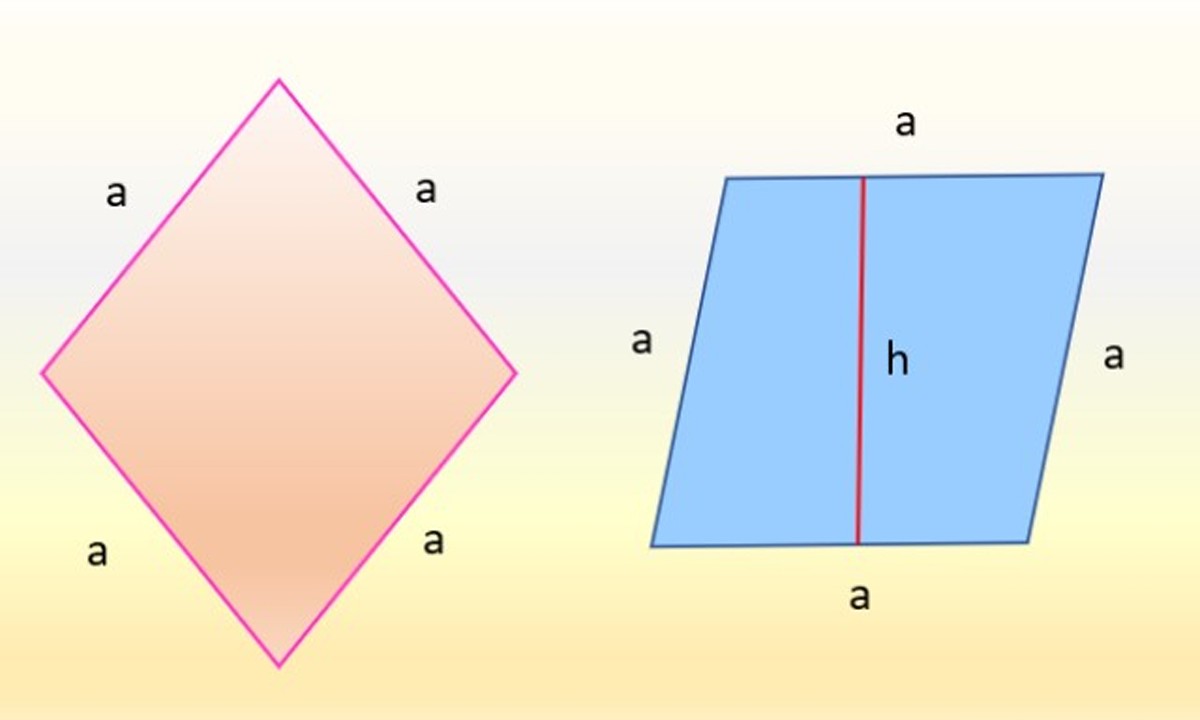
Resulta que las figuras son idénticas, porque lo que ha cambiado es solo la orientación. El rombo de la izquierda, en rosa, cuyos lados tienen la misma medida: a, se gira de tal forma que uno de sus lados quede completamente horizontal. Entonces, el rombo toma la forma del paralelogramo azul de la derecha.

Y el área de este paralelogramo es también el producto entre la base “a” y la altura respecto a esa base, llamada “h” en la figura, por lo tanto:

A _{paralelogramo} = a × h

Ya que se trata de la misma figura, el área es idéntica y se sigue que:

A _rombo = a × h

Así, conociendo a y h del paralelogramo, se calcula su área y esta coincidirá con la del rombo.

Área del rombo inscrito en un rectángulo

Otra relación entre rombo y rectángulo aparece cuando el primero se inscribe en el interior del segundo. Si esto sucede, los vértices del rombo coinciden con el punto medio de los lados del rectángulo, lo cual se visualiza a continuación:

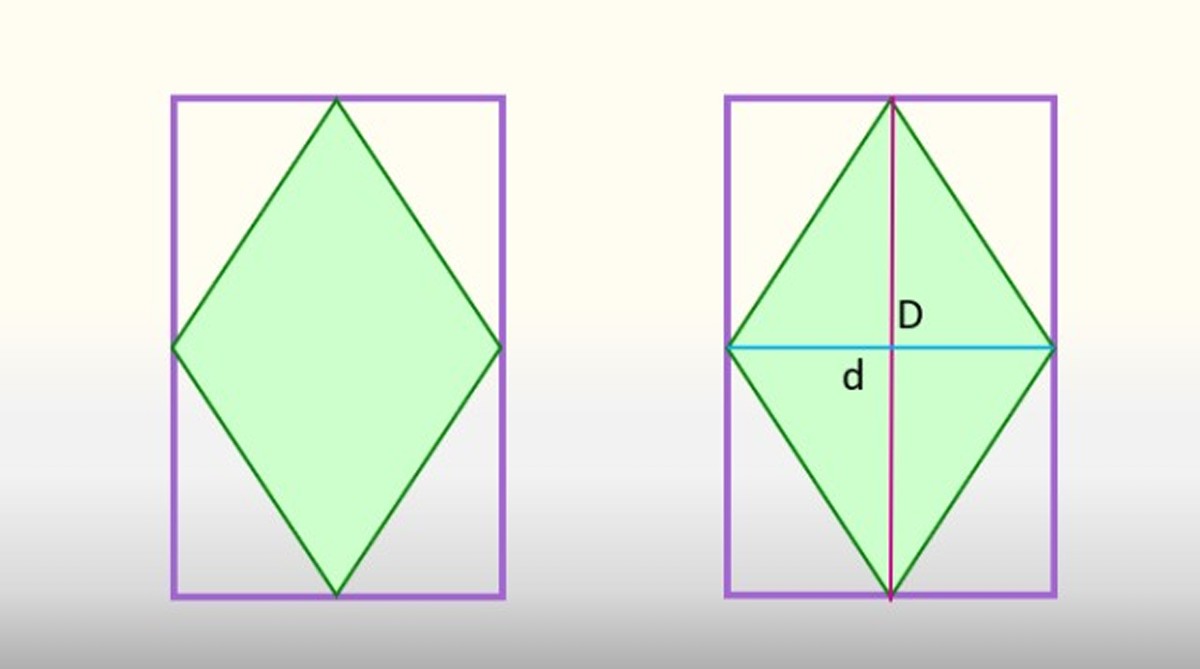
Esta disposición hace que al dibujar las diagonales mayor y menor del rombo, la figura se divida en 8 triángulos idénticos, 4 de los cuales corresponden al rombo, en verde, y los otros 4 forman parte del rectángulo. Si estos últimos 4 triángulos se unieran, formarían la mitad del rectángulo, y los 4 triángulos del rombo, la otra.

Por lo tanto, el área del rombo equivale a la mitad del área del rectángulo en el que está inscrito, afirmándose que:

A_rombo = A_rectángulo / 2

Esto se comprueba fácilmente calculando el área de uno de los triángulos y multiplicando por 4, puesto que son idénticos. El área de un triángulo cualquiera es la mitad del producto entre base y su altura:

A _triángulo = base × altura /2

De la figura anterior se observa que la base de uno de los triángulos es d/2 y la altura es D/2, que sustituyendo en la fórmula anterior da:

A _triángulo = (d/2) × (D/2) /2 = (d×D) /8

Multiplicando este resultado por 4 para tener el área del rombo:

A _rombo = 4 (d×D) /8 = (d×D) /2

Por su parte, el área de la mitad del rectángulo es:

A _rectángulo / 2 = base × altura / 2

Como la base del rectángulo es d y su altura es D, queda:

A_rectángulo / 2 = d × D/ 2

Que es precisamente el área del rombo inscrito. Se concluye entonces que:

El área de un rombo inscrito en un rectángulo equivale a la mitad del área de este.

Ejercicios resueltos

Ejercicio 1

¿Cuánto vale el área del rombo cuya diagonal mayor mide 14.6 cm y la diagonal menor 9.8 cm?

Solución

Mediante sustitución de D= 14.6 cm y d= 9.8 cm en la fórmula del área del rombo:

El área buscada resulta:

A _rombo = 14.6 cm × 9.8 cm= 143.1 cm²

Ejercicio 2

En la figura de la sección precedente, la diagonal mayor del rombo inscrito en el rectángulo mide D= 30 cm y el área del rectángulo vale 210 cm². Se pide calcular:

a) La longitud de la diagonal menor

b) El área del rombo, de dos formas: la primera a través del área del rectángulo y la segunda utilizando la fórmula del área de un rombo. Comprobar que el resultado es el mismo.

Solución a

El área del rectángulo es el producto entre su base y su altura. La diagonal mayor D es su altura, mientras que la diagonal menor d sería la base. Empleando la fórmula del área y sustituyendo los valores del enunciado, se tiene:

A _rectángulo = base × altura = d × 30 cm = 210 cm²

Entonces la base vale:

d= 210 cm² / 30 cm = 7 cm

Solución b

De acuerdo a lo visto anteriormente, el área del rombo es la mitad del área del rectángulo, y esta es conocida:

A _rombo = 210 cm² /2 = 105 cm²

Enseguida se comprueba el resultado, sustituyendo en la fórmula:

Las diagonales ya son conocidas: D= 30 cm, d= 7 cm, entonces:

A _rombo = 30 cm × 7 cm /2 = 105 cm²

Se comprueba que, según lo esperado, el área del rombo es la misma en los dos casos.