Tiro parabólico: características, fórmulas y ecuaciones, ejemplos

El tiro parabólico consiste en arrojar un objeto o proyectil con cierto ángulo y dejar que se mueva bajo la acción de la gravedad. Si no se considera la resistencia del aire, el objeto, sin importar su naturaleza, seguirá una trayectoria en forma de arco de parábola.

Se trata de un movimiento cotidiano, ya que entre los deportes más populares están aquellos en que se arrojan pelotas o balones, ya sea con la mano, con el pie o con algún instrumento como una raqueta o un bate por ejemplo.

Para su estudio, el tiro parabólico se desglosa en dos movimientos superpuestos: uno horizontal sin aceleración, y el otro vertical con aceleración constante hacia abajo, que es la gravedad. Ambos movimientos poseen velocidad inicial.

Digamos que el movimiento horizontal transcurre a lo largo del eje x y el vertical a lo largo del eje y. Cada uno de estos movimientos es independiente del otro.

En vista de que determinar la posición del proyectil es el principal objetivos, es necesario escoger un sistema de referencia apropiado. Los detalles vienen a continuación.

Índice del artículo

• 1 Fórmulas y ecuaciones del tiro parabólico
  • 1.1 – Trayectoria, altura máxima, tiempo máximo y alcance horizontal
• 2 Ejemplos de tiro parabólico
  • 2.1 Tiro parabólico en actividades humanas
  • 2.2 El tiro parabólico en la naturaleza
• 3 Ejercicio
• 4 Referencias

Fórmulas y ecuaciones del tiro parabólico

Supongamos que el objeto se lanza con ángulo α respecto a la horizontal y velocidad inicial v_o como se muestra en la figura de abajo a la izquierda. El tiro parabólico es un movimiento que transcurre sobre el plano xy y en ese caso la velocidad inicial se descompone así:

v_ox = v_o cos α

v_oy = v_o sen α

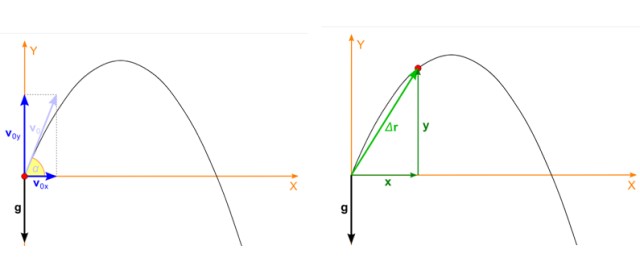
La posición del proyectil, que es el punto rojo en la figura 2, imagen derecha, también tiene dos componentes que dependen del tiempo, una en x y la otra en y. La posición es un vector al que se denota como r y sus unidades son de longitud.

En la figura, la posición inicial del proyectil coincide con el origen del sistema de coordenadas, por lo tanto x_o = 0, y_o = 0. No siempre sucede así, se puede escoger el origen en cualquier parte, pero esta elección simplifica mucho los cálculos.

En cuanto a los dos movimientos en x y en y, estos son:

-x(t): es un movimiento rectilíneo uniforme.

-y(t): corresponde a un movimiento rectilíneo uniformemente acelerado con g = 9.8 m/s² y apuntando verticalmente hacia abajo.

En forma matemática:

x (t) = v_o cos α.t

y (t) =v_o .sen α.t – ½g.t²

El vector de posición queda:

r (t) = [v_o cos α.t]i + [v_o .sen α.t – ½g.t²] j

En estas ecuaciones el lector atento notará que el signo menos se debe a que la gravedad apunta hacia el suelo, el sentido elegido como negativo, mientras que hacia arriba se toma como positivo.

Dado que la velocidad es la primera derivada de la posición, basta con derivar r (t) respecto al tiempo y obtener:

v (t) = v_o cos α i + (v_o .sen α – gt) j

Por último la aceleración se expresa vectorialmente como:

 a (t) = -g j

– Trayectoria, altura máxima, tiempo máximo y alcance horizontal

Trayectoria

Para encontrar la ecuación explícita de la trayectoria, que es la curva y(x), hay que eliminar el parámetro tiempo, despejando en la ecuación para x(t) y sustituyendo en y(t). La simplificación es un tanto laboriosa, pero finalmente se obtiene:

Altura máxima

La altura máxima ocurre cuando v_y = 0. Sabiendo que existe la siguiente relación entre posición y el cuadrado de la velocidad:

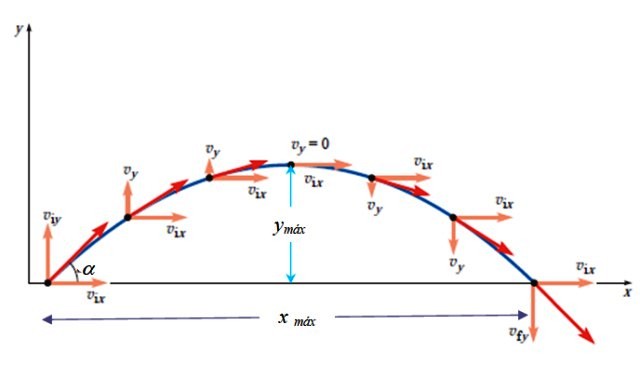
v_y² = v_oy ²– 2gy

Haciendo v_y = 0 justo al llegar a la altura máxima:

 0 = v_oy ²– 2g.y_máx → y_máx = v_oy ²/2g

Con:

v_oy = v_o senα

Tiempo máximo

El tiempo máximo es el tiempo que el objeto demora en llegar a y_máx. Para calcularlo se utiliza:

v_y = v_o .sen α – gt

Sabiendo que v_y se hace 0 cuando t = t_máx, resulta:

v_o .sen α – g.t_máx = 0

t_máx = v_oy /g

Alcance horizontal máximo y tiempo de vuelo

El alcance es muy importante, porque señala dónde caerá el objeto. Así sabremos si da o no en el blanco. Para encontrarlo necesitamos el tiempo de vuelo, tiempo total o t_v.

De la ilustración anterior es fácil concluir que t_v = 2.t_máx. Pero ¡atenciónǃ solamente es verdad si el lanzamiento es a nivel, es decir, la altura del punto de partida es la misma que la altura de la llegada. De lo contrario el tiempo se encuentra resolviendo la ecuación de segundo grado que resulta de sustituir la posición final y_final:

y_final = v_o .sen α.t_v – ½g.t_v²

En todo caso el alcance horizontal máximo es:

x_máx = v_ox. t_v

Ejemplos de tiro parabólico

El tiro parabólico forma parte del movimiento de personas y animales. También de casi todos los deportes y los juegos donde la gravedad interviene. Por ejemplo:

Tiro parabólico en actividades humanas

-La piedra arrojada por una catapulta.

-El saque de meta del portero.

-La pelota que lanza el pitcher.

-La flecha que sale del arco.

-Todo tipo de saltos

-Lanzar una piedra con una honda.

-Cualquier arma arrojadiza.

El tiro parabólico en la naturaleza

-El agua que brota de los chorros naturales o artificiales como los de una fuente.

-Piedras y lava brotando de un volcán.

-Una pelota que rebota en el pavimento o una piedra que lo hace sobre el agua.

-Toda clase de animales que saltan: canguros, delfines, gacelas, felinos, ranas, conejos o insectos, por mencionar unos pocos.

Ejercicio

Un saltamontes salta formando ángulo de 55 º con la horizontal y aterriza a 0.80 metros más adelante. Encontrar:

a) La altura máxima alcanzada.

b) Si saltara con la misma velocidad inicial, pero formando ángulo de 45º, ¿llegaría más alto?

c) ¿Qué se puede decir del alcance horizontal máximo para este ángulo?

Solución a

Cuando los datos suministrados por el problema no contienen la velocidad inicial v_o los cálculos son algo más laboriosos, pero a partir de las ecuaciones conocidas, se puede deducir una nueva expresión. Partiendo de:

x_máx = v_ox . t_vuelo = v_o.cos α. t_v

Cuando aterriza más adelante, la altura vuelve a ser 0, entonces:

v_o .sen α.t_v – ½g.t_v²= 0

Como t_v es factor común, se simplifica:

v_o .sen α – ½g.t_v= 0

Podemos despejar t_v de la primera ecuación:

t_v = x_máx / v_o.cos α

Y sustituir en la segunda:

v_o .sen α – (½g.x_máx / v_o.cos α)= 0

Al multiplicar todos los términos por v_o.cos α la expresión no se altera y el denominador desaparece: 

(v_o .sen α.) (v_o.cos α) – ½g.x_máx = 0

v_o² sen α. cos α = ½g.x_máx

Ya puede despejarse v_o o también sustituir la siguiente identidad:

sen 2α = 2 sen α. cos α → v_o² sen 2α = g.x_máx

Se calcula v_o²:

v_o² = g.x_máx / sen 2α = (9.8 x 0.8 / sen 110) m²/s² = 8.34 m²/s²

Y finalmente la altura máxima:

 y_máx= v_oy ²/2g = (8.34 x sen² 55)/(2 x 9.8) m = 0.286 m = 28.6 cm

 Solución b

La langosta se las arregla para mantener la misma velocidad horizontal, pero al disminuir el ángulo:

 y_máx= v_oy ²/2g = (8.34 x sen² 45)/(2 x 9.8) m = 0.213 m = 21.3 cm

Alcanza una altura menor.

Solución c

El alcance máximo horizontal es:

x_máx = v_o² sen 2a / g

Al variar el ángulo también cambia el alcance horizontal:

 x_máx = 8.34 sen 90 / 9.8  m = 0.851 m = 85.1 cm

El salto es más largo ahora. El lector puede comprobar que es máximo para el ángulo de 45 º pues:

sen 2α = sen 90 = 1.

Referencias

1. Figueroa, D. 2005. Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
2. Giambattista, A. 2010. Physics. Second Edition. McGraw Hill.
3. Giancoli, D.  2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
4. Resnick, R. 1999. Física. Vol. 1. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V.
5. Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.