Eneágono: propiedades, cómo hacer un eneágono, ejemplos
Un eneágono es un polígono de nueve lados y nueve vértices, el cual puede ser regular o no. La denominación eneágono proviene del griego y se compone de las palabras griegas ennea (nueve) y gonon (ángulo).
Un nombre alternativo para el polígono de nueve lados es nonágono palabra que proviene del latín nonus (nueve) y gonon (vértice). Por otra parte, si los lados o los ángulos del eneágono son desiguales entre sí, se tiene entonces un eneágono irregular. Si por el contrario, los nueve lados y los nueve ángulos del eneágono son iguales, entonces se trata de un eneágono regular.
Índice del artículo
Para un polígono de n lados la suma de sus ángulos internos es:
(n – 2) * 180º
En el eneágono sería n=9, por lo que la suma de sus ángulos internos es:
Sa = (9 – 2) * 180º = 7 * 180º = 1260º
En cualquier polígono, el número de diagonales es:
D = n ( n – 3 ) / 2 y en el caso del eneágono, como n = 9, se tiene entonces que D = 27.
En el eneágono o nonágono regular se tienen nueve (9) ángulos internos de igual medida, por lo tanto cada ángulo mide la novena parte de la suma total de los ángulos internos.
Se tiene entonces que la medida de los ángulos internos de un eneágono es 1260º / 9 = 140º.
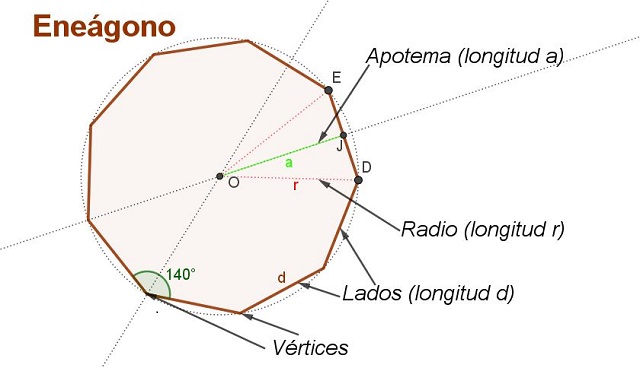
Para deducir la fórmula del área de un eneágono regular de lado d es conveniente hacer algunas construcciones auxiliares, como las mostradas en la figura 2.
Se encuentra el centro O trazando las mediatrices de dos lados adyacentes. El centro O equidista de los vértices.
Un radio de longitud r es el segmento que va del centro O a un vértice del eneágono. En la figura 2 se muestran los radios OD y OE de longitud r.
El apotema es el segmento que va del centro hasta el punto medio de un lado del eneágono. Por ejemplo OJ es un apotema cuya longitud es a.
Consideramos el triángulo ODE de la figura 2. El área de este triángulo es el producto de su base DE por la altura OJ dividida entre 2:
Área ODE = (DE * OJ) / 2 = ( d * a ) / 2
Como hay 9 triángulos de igual área en el eneágono, se concluye entonces que el área del mismo es:
Área del eneágono = (9/2)(d * a)
Si solamente se conoce la longitud d de los lados del eneágono, es necesario entonces hallar la longitud del apotema para poder aplicar la fórmula del apartado anterior.
Consideramos el triángulo OJE rectángulo en J (ver figura 2). Si se aplica la razón trigonométrica tangente se obtiene:
tan(∡OEJ) = OJ / EJ.
El ángulo ∡OEJ = 140º / 2 = 70º, por ser EO bisectriz del ángulo interno del eneágono.
Por otra parte, OJ es el apotema de longitud a.
Luego, como J es punto medio de ED se deduce que EJ = d/2.
Sustituyendo los valores anteriores en la relación de la tangente se tiene:
tan(70º) = a / (d/2).
Ahora despejamos la longitud del apotema:
a = (d/2) tan(70º).
Se sustituye el resultado previo en la fórmula del área para obtener:
Área del eneágono = (9/2)( d * a ) = (9/2)( d * (d/2) tan(70º) )
Finalmente se encuentra la fórmula que permite obtener el área del eneágono regular si solo se conoce la longitud d de sus lados:
Área del eneágono = (9/4) d2 tan(70º) = 6,1818 d2
El perímetro de un polígono es la suma de sus lados. En el caso del eneágono, como todos y cada uno de los lados mide una longitud d, su perímetro será la suma de nueve veces d, es decir:
Perímetro = 9 d
Considerando el triángulo OJE rectángulo en J (ver figura 2), se aplica la razón trigonométrica coseno:
cos(∡OEJ) = EJ / OE = (d/2) / r
De donde se obtiene:
d = 2r cos(70º)
Sustituyendo este resultado se obtiene la fórmula del perímetro como función del radio de eneágono:
Perímetro = 9 d = 18 r cos(70º) = 6,1564 r
1- Para construir un eneágono regular, con regla y compás, se parte de la circunferencia c que circunscribe al eneágono. (ver figura 3)
2- Se trazan dos rectas perpendiculares que pasen por el centro O de la circunferencia. Luego se marcan las intersecciones A y B de una de las rectas con la circunferencia.
3- Con el compás, haciendo centro en la intercepción B y apertura igual al radio BO se traza un arco que intercepte a la circunferencia original en un punto C.
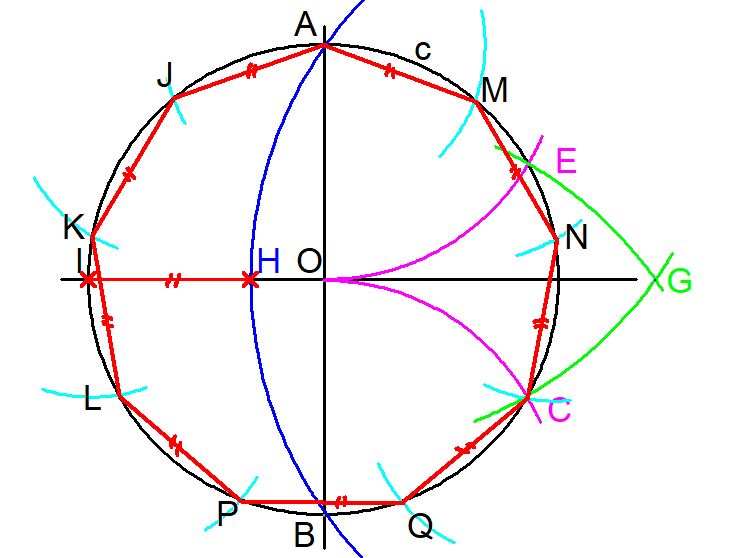
4- Se repite el paso anterior pero haciendo centro en A y radio AO se traza un arco que intercepta a la circunferencia c en el punto E.
5- Con apertura AC y centro en A se traza un arco de circunferencia. Similarmente con apertura BE y centro B se traza otro arco. Se marca la intersección de estos dos arcos como punto G.
6- Haciendo centro en G y con apertura GA se traza un arco que intercepta al eje secundario (horizontal en este caso) en el punto H. Se marca la intersección del eje secundario con la circunferencia original c como I.
7- La longitud del segmento IH es igual a la longitud d del lado del eneágono.
8- Con apertura de compás IH = d se trazan sucesivamente los arcos de centro A radio AJ, centro J radio AK, centro K radio KL y centro L radio LP.
9- Similarmente, partiendo de A y por el lado derecho, se trazan arcos de radio IH = d que marcan sobre la circunferencia original c los puntos M, N, C y Q.
10- Finalmente se trazan los segmentos AJ, JK, KL, LP, AM, MN, NC, CQ y por último PB.
Cabe destacar que el método de construcción no es del todo exacto, ya que puede comprobarse que el último lado PB es 0,7% más largo que los otros lados. Hasta la fecha no se conoce un método de construcción con regla y compás que sea 100% preciso.
A continuación se abordarán algunos ejemplos resueltos.
Se quiere construir un eneágono regular cuyos lados midan 2 cm. ¿Qué radio ha de tener la circunferencia que lo circunscribe, de modo que al aplicar la construcción descrita previamente se obtenga el resultado deseado?
Solución:
En un apartado anterior se dedujo la fórmula que relaciona el radio r de la circunferencia circunscrita con el lado d de un eneágono regular:
d = 2r cos(70º)
Despejando r de la expresión anterior nos queda:
r = d / (2 cos(70º) ) = 1,4619 * d
Sustituyendo el valor d= 2 cm en la fórmula previa se obtiene un radio r de 2,92 cm.
¿Cuánto vale el área de un eneágono regular de 2 cm de lado?
Solución:
Para responder esta pregunta hay que remitirse a la fórmula, demostrada previamente, que permite hallar el área de un eneágono conocido la longitud d de su lado:
Área del eneágono = (9/4) d2 tan(70º) = 6,1818 d2
Sustituyendo d por su valor de 2 cm en la fórmula anterior se obtiene:
Área del eneágono = 24,72 cm
- C. E. A. (2003). Elementos de geometría: con ejercicios y geometría del compás. Universidad De Medellín.
- Campos, F., Cerecedo, F. J. (2014). Matemáticas 2. Grupo Editorial Patria.
- Freed, K. (2007). Discover Polygons. Benchmark Education Company.
- Hendrik, V. (2013). Generalized Polygons. Birkhäuser.
- IGER. (s.f.). Matemática Primer Semestre Tacaná. IGER.
- Jr. geometry. (2014). Polygons. Lulu Press, Inc.
- Miller, Heeren, & Hornsby. (2006). Matemática: Razonamiento Y Aplicaciones (Décima Edición). Pearson Educación.
- Patiño, M. (2006). Matemáticas 5. Editorial Progreso.
