Propiedad asociativa: suma, multiplicación, ejemplos, ejercicios
La propiedad asociativa de la suma representa el carácter asociativo de la operación suma en diversos conjuntos matemáticos. En ella se relacionan tres (o más) elementos de dichos conjuntos, llamados a, b y c, tales que siempre se cumple:
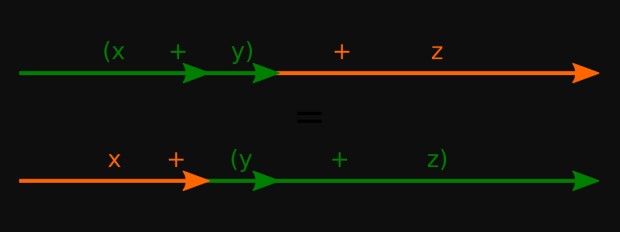
a + (b+c) = (a + b) +c
De esta manera se garantiza que, sin importar la manera de agrupar para llevar a cabo la operación, el resultado es el mismo.

Pero hay que destacar que la propiedad asociativa no es sinónimo de propiedad conmutativa. Es decir, sabemos que el orden de los sumandos no altera la suma o que el orden de los factores no altera el producto. Entonces para la suma se puede escribir así: a + b = b + a.
Sin embargo, en la propiedad asociativa es diferente, ya que el orden de los elementos a sumar se mantiene y lo que cambia es la operación que se ejecuta primero. Lo que significa que da igual sumar primero (b+c) y a este resultado agregarle a, que empezar sumando a con b y al resultado añadir c.
Muchas operaciones importantes como la suma son asociativas, pero no todas. Por ejemplo en la resta de números reales ocurre que:
a – (b – c) ≠ (a – b) – c
Si a = 2, b = 3, c= 1, entonces:
2– (3 – 1) ≠ (2 – 3) – 1
0 ≠ -2
Índice del artículo
Tal como se hizo para la suma, la propiedad asociativa de la multiplicación señala que:
a ˟ (b ˟ c) = (a ˟ b) ˟ c
En el caso del conjunto de los números reales es sencillo verificar que siempre es así. Por ejemplo, usando los valores a = 2, b = 3, c= 1, se tiene que:
2 ˟ (3 ˟ 1) = (2 ˟ 3) ˟ 1 → 2 ˟ 3 = 6 ˟ 1
6 = 6
Los números reales cumplen la propiedad asociativa tanto de la suma como de la multiplicación. En cambio en otro conjunto, como el de los vectores, la suma es asociativa, pero el producto cruz o producto vectorial no lo es.
Una ventaja que tienen las operaciones en las que se cumple la propiedad asociativa es la de poder agrupar de la manera más conveniente. Esto facilita mucho la resolución.
Por ejemplo, supongamos que en una pequeña biblioteca hay 3 estantes con 5 entrepaños cada una. En cada entrepaño hay 8 libros. ¿Cuántos libros hay en total?
Podemos efectuar la operación así: total de libros = (3 x 5) x 8 = 15 x 8 = 120 libros.
O bien así: 3 x (5 x 8) = 3 x 40 = 120 libros.

-En los conjuntos de números naturales, enteros, racionales, reales y complejos se cumplen la propiedad asociativa de la suma y de la multiplicación.
-Para los polinomios también aplican en dichas operaciones.
-En los casos de operaciones de resta, división y exponenciación, la propiedad asociativa no se cumple ni en números reales ni polinomios.
-En el caso de las matrices, la propiedad asociativa se cumple para la suma y la multiplicación, aunque en este último caso, no se cumple la conmutatividad. Esto significa que, dadas las matrices A, B y C, es verdad que:
(A x B) x C = A x (B x C)
Pero… A x B ≠ B x A
Los vectores forman un conjunto diferente que los números reales o los números complejos. Las operaciones definidas para el conjunto de los vectores son un tanto diferentes: hay suma, resta y tres tipos de productos.
La suma de vectores cumple la propiedad asociativa, al igual que los números, los polinomios y las matrices. En cuanto a los productos escalar, escalar por vector y cruz que se realizan entre vectores, este último no la cumple, pero el producto escalar, que es otra clase de operación entre vectores, sí la cumple, tomando en cuenta lo siguiente:
-El producto de un escalar por un vector da como resultado un vector.
-Y al multiplicar escalarmente dos vectores, resulta un escalar.
Por lo tanto, dados los vectores v, u y w, y adicionalmente un escalar λ, es posible escribir:
–Suma de vectores: v +(u + w ) = (v + u) + w
-Producto escalar: λ(v • u ) = (λv) • u
Esto último es posible gracias a que v • u resulta un escalar, y λv es un vector.
Sin embargo:
v ×(u × w ) ≠ (v × u)×w
Esta aplicación es muy interesante, porque tal como se dijo anteriormente, la propiedad asociativa ayuda a resolver ciertos problemas. La suma de monomios es asociativa y esto se puede utilizar para factorizar cuando a primera vista no aparezca un factor común obvio.
Por ejemplo, supongamos que se pide factorizar: x3 + 2x2 + 3x +6. Este polinomio carece de factor común, pero veamos lo que sucede si se agrupa de esta manera:
x3 + 2x2 + 3x +6 = (x3 + 2x2) + (3x +6)
El primer paréntesis tiene como factor común a x2:
x3 + 2x2 = x2 (x+2)
En el segundo el factor común es 3:
3x +6 = 3(x+ 2)
Entonces:
x3 + 2x2 + 3x +6 = x2(x+2)+ 3(x+ 2)
Ahora sí hay un factor común obvio, que es x+2:
x2(x+2)+ 3(x+ 2) = (x+2)( x2+3)
El edificio de un colegio tiene 4 pisos y en cada uno hay 12 aulas con 30 pupitres en su interior. ¿Cuántos pupitres tiene el colegio en total?
Solución
Este problema se resuelve aplicando la propiedad asociativa de la multiplicación, veamos:
Número total de pupitres = 4 pisos x 12 aulas/piso x 30 pupitres /aula = (4 x 12) x 30 pupitres = 48 x 30 = 1440 pupitres.
O si se prefiere: 4 x (12 x 30) = 4 x 360 = 1440 pupitres
Dados los polinomios:
A(x) = 5x3 + 2x2 -7x + 1
B(x) = x4 +6x3 -5x
C(x) = -8x2 +3x -7
Aplicar la propiedad asociativa de la suma para encontrar A(x) + B(x) + C(x).
Solución
Se pueden agrupar los dos primeros y al resultado sumar el tercero:
A(x) + B(x) = [5x3 + 2x2 -7x + 1] + [x4 +6x3 -5x] = x4 + 11x3+ 2x2 -12x +1
De inmediato se agrega el polinomio C(x):
[x4 + 11x3+ 2x2 -12x +1]+ [-8x2 +3x -7] = x4 + 11x3 – 6x2 -9x -6
El lector puede comprobar que el resultado es idéntico si se resuelve mediante la opción A(x) + [B(x) + C(x)].
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Math is Fun. Commutative, Associative and Distributive Laws. Recuperado de: mathisfun.com.
- Math Warehouse. Definition of Associative Property. Recuperado de: mathwarehouse.com.
- Sciencing. Associative & Commutative Property of Addition & Multiplication (With Examples). Recuperado de: sciencing.com.
- Wikipedia. Associative property. Recuperado de: en.wikipedia.org.
