Línea perpendicular: características, ejemplos, ejercicios
Una línea perpendicular es aquella que forma un ángulo de 90º respecto a otra línea, curva o superficie. Nótese que cuando dos líneas son perpendiculares y están sobre un mismo plano, al cortarse forman cuatro ángulos idénticos, cada uno de 90º.
Si uno de los ángulos no es 90º se dice que las líneas son oblicuas. Las líneas perpendiculares son frecuentes en diseño, arquitectura y construcción, por ejemplo la red de tuberías de la siguiente imagen.

La orientación de las líneas perpendiculares puede ser diversa, como por ejemplo las que se muestran a continuación:
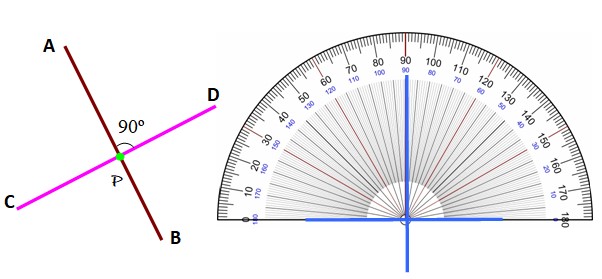
Independientemente de la posición, las líneas perpendiculares entre sí se reconocen al identificar el ángulo entre ellas como 90º, con ayuda del transportador.
Obsérvese que a diferencia de las líneas paralelas en el plano, que nunca se intersectan, las perpendiculares siempre lo hacen en un punto P, llamado pie de una de las líneas sobre la otra. Por lo tanto dos líneas perpendiculares también son secantes.
Una línea cualquiera posee infinitas perpendiculares a ella, ya que con solo desplazar el segmento AB a la izquierda o la derecha sobre el segmento CD, tendremos nuevas perpendiculares con otro pie.
Sin embargo, a la perpendicular que pasa justo por el punto medio de un segmento se le llama bisectriz de dicho segmento.
Índice del artículo
Las líneas perpendiculares son frecuentes en el paisaje urbano. En la siguiente imagen (figura 3) se han destacado apenas unas pocas de las muchas líneas perpendiculares que se aprecian en la sencilla fachada de esta edificación y sus elementos como puertas, ductos, escalones y más:

Lo bueno es que tres rectas perpendiculares entre sí nos ayudan a establecer la ubicación de los puntos y objetos en el espacio. Son los ejes coordenados identificados como eje x, eje y y eje z, claramente visibles en la esquina de una habitación rectangular como la que sigue:
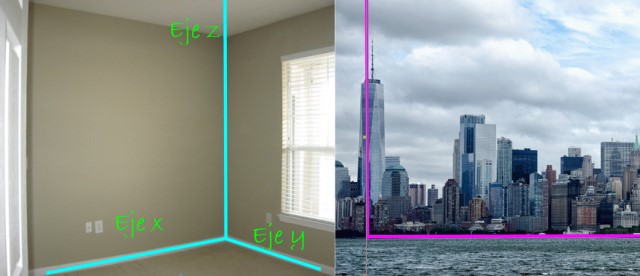
En la panorámica de la ciudad, a la derecha, también se advierte la perpendicularidad entre el rascacielos y el suelo. El primero diríamos que se encuentra a lo largo del eje z, mientras que el suelo es un plano, que en este caso es el plano xy.
Si el suelo constituye el plano xy, el rascacielos también es perpendicular a cualquier avenida o calle, lo cual garantiza su estabilidad, ya que una estructura inclinada es inestable.
Y en las calles, donde quiera que haya esquinas rectangulares, hay líneas perpendiculares. Muchas avenidas y calles tienen un trazado perpendicular, siempre que el terreno y los accidentes geográficos lo permitan.
Para expresar abreviadamente la perpendicularidad entre rectas, segmentos o vectores, se utiliza el símbolo ⊥. Por ejemplo, si la recta L1 es perpendicular a la recta L2, escribimos:
L1 ⊥ L2
– En el diseño las líneas perpendiculares están muy presentes, ya que muchos objetos comunes se basan en cuadrados y rectángulos. Estos cuadriláteros se caracterizan por tener ángulos internos de 90º, porque sus lados son paralelos dos a dos:
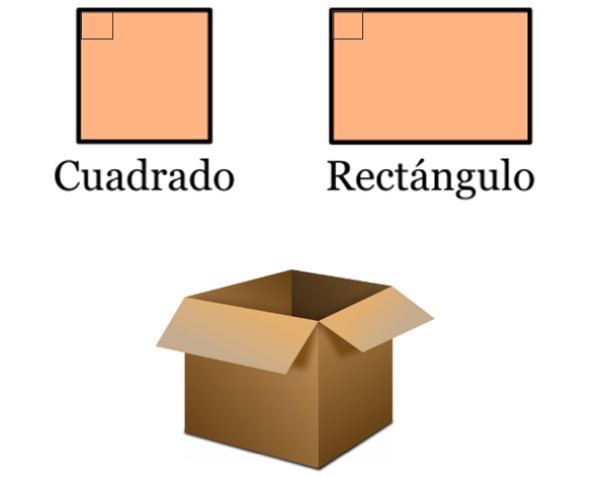
– Las canchas en las que se practican distintos deportes están demarcadas por numerosos cuadrados y rectángulos. Estos a su vez contienen líneas perpendiculares.
– Dos de los segmentos que componen un triángulo rectángulo son perpendiculares entre sí. A estos se les llama catetos, mientras que la línea restante se denomina hipotenusa.
– Las líneas del vector campo eléctrico son perpendiculares a la superficie de un conductor en equilibrio electrostático.
– Para un conductor cargado, las líneas y superficies equipotenciales siempre son perpendiculares a las de campo eléctrico.
– En los sistemas de tuberías o conductos empleados para transportar diferentes clases de fluidos, como las de gas que aparecen en la figura 1, es frecuente que se presenten codos en ángulo recto. Por lo tanto forman líneas perpendiculares, tal es el caso de una sala de calderas:

Dibujar dos líneas perpendiculares mediante regla y compás.
Solución
Es muy sencillo de hacer, siguiendo estos pasos:
-Se dibuja la primera línea, llamada AB (negro).
-Por encima (o por debajo si se prefiere) de AB se marca el punto P, por donde va a pasar la perpendicular. Si P está justo encima (o por debajo) de la mitad de AB, dicha perpendicular es la bisectriz del segmento AB.
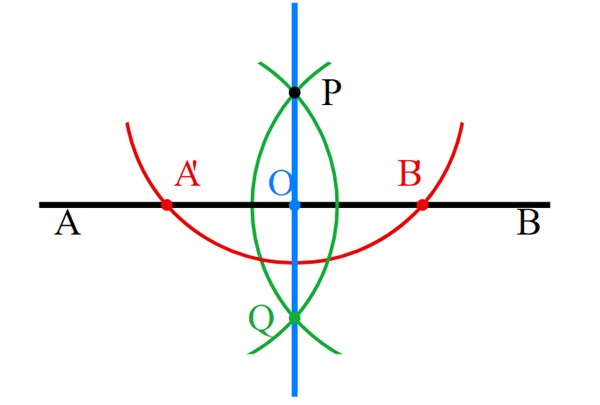
-Con el compás centrado en P se traza una circunferencia que corte a AB en dos puntos, llamados A’ y B’ (rojo).
-Se apertura el compás en A’P, se centra en A’ y se traza una circunferencia que pase por P (verde).
-Repetir el paso anterior, pero ahora aperturando el compás el largo del segmento B’P (verde). Ambos arcos de circunferencia se cortan en el punto Q por debajo de P y desde luego en este último.
-Se unen los puntos P y Q con la regla y ya está lista la línea perpendicular (azul).
-Por último hay que borrar cuidadosamente todas las construcciones auxiliares, dejando solo las perpendiculares.
Dos rectas L1 y L2 son perpendiculares si sus respectivas pendientes m1 y m2 cumplen esta relación:
m1 = -1/m2
Dada la recta y = 5x – 2, encontrar una recta perpendicular a ella y que pase por el punto (-1, 3).
Solución
-En primer lugar se encuentra la pendiente de la recta perpendicular m⊥, según lo indicado en el enunciado. La pendiente de la recta original es m = 5, el coeficiente que acompaña a “x”. Entonces:
m⊥= -1/5
-Luego se construye la ecuación de la recta perpendicular y⊥, sustituyendo el valor previamente encontrado:
y⊥= -1/5x + b
-Seguidamente se determina el valor de b, con ayuda del punto dado por el enunciado, el (-1,3), ya que la recta perpendicular debe pasar por él:
y = 3
x = -1
Sustituyendo:
3 = -1/5(-1) + b
Se despeja el valor de b:
b = 3- (1/5) = 14/5
-Por último se construye la ecuación definitiva:
y⊥= -1/5x + 14/5
- Baldor, A. 2004. Geometría plana y del espacio. Publicaciones Cultural.
- Clemens, S. 2001. Geometría con aplicaciones y solución de problemas. Addison Wesley.
- Math is Fun. Perpendicular lines. Recuperado de: mathisfun.com.
- Monterey Institute. Líneas perpendiculares. Recuperado de: montereyinstitute.org.
- Wikipedia. Líneas perpendiculares. Recuperado de: es.wikipedia.org.
