Ley de Faraday: fórmula, unidades, experimentos, ejercicio,
La ley de Faraday en electromagnetismo establece que un flujo de campo magnético cambiante es capaz de inducir una corriente eléctrica en un circuito cerrado.
En 1831, el físico inglés Michael Faraday experimentó moviendo conductores en el interior de un campo magnético y también variando campos magnéticos que atravesaban conductores fijos.
Faraday se dio cuenta de que si hacía variar el flujo de campo magnético en el tiempo, era capaz de establecer un voltaje proporcional a dicha variación. Si ε es el voltaje o fuerza electromotriz inducida (fem inducida) y Φ es el flujo de campo magnético, en forma matemática se puede expresar:
|ε| = ΔΦ/Δt
Donde el símbolo Δ indica variación de la cantidad y las barras en la fem indican el valor absoluto de esta. Puesto que se trata de un circuito cerrado, la corriente puede circular en un sentido o en otro.
El flujo magnético, producido por un campo magnético a través de una superficie, puede variar de diversas formas, por ejemplo:
-Moviendo un imán de barra a través de una espira circular.
-Aumentando o disminuyendo la intensidad del campo magnético que atraviesa la espira.
-Dejando fijo el campo, pero mediante algún mecanismo cambiar el área de la espira.
-Combinando los métodos anteriores.

Índice del artículo
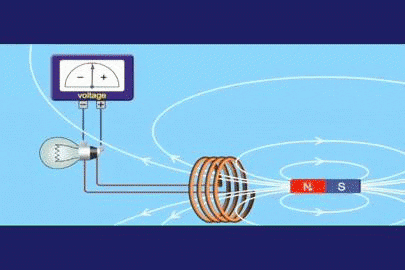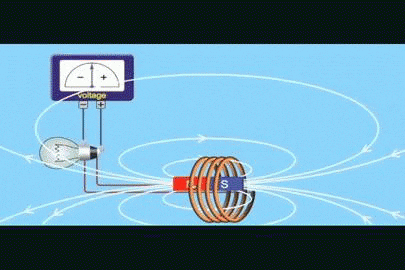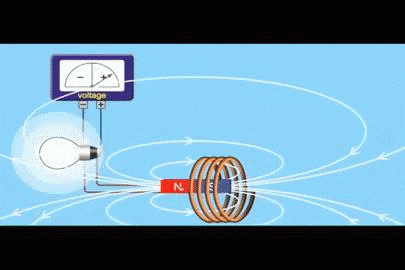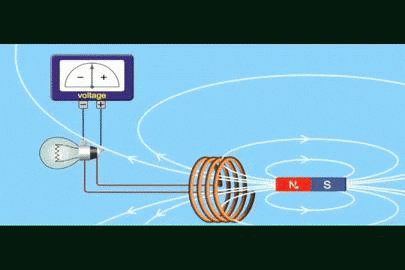
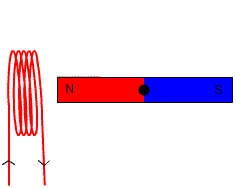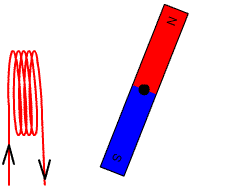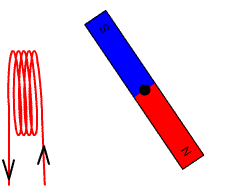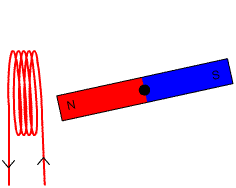
Supongamos que se tiene un circuito cerrado de área A, como una espira circular o un embobinado igual al de la figura 1, y que se tiene un imán que produce un campo magnético B.
El flujo de campo magnético Φ es una cantidad escalar que se refiere a la cantidad de líneas de campo que atraviesan el área A. En la figura 1 son las líneas blancas que salen del polo norte del imán y retornan por el sur.
La intensidad del campo será proporcional al número de líneas por unidad de área, así que podemos ver que en los polos es muy intenso. Pero podemos tener un campo muy intenso que no produzca flujo en la espira, cosa que podemos lograr cambiando la orientación de esta (o del imán).
Para tomar en cuenta el factor orientación, el flujo de campo magnético se define como el producto escalar entre B y n, siendo n el vector normal unitario a la superficie de la espira y que señala su orientación:
Φ = B•n A =BA.cosθ
Donde θ es el ángulo entre B y n. Si por ejemplo B y n son perpendiculares, el flujo de campo magnético es nulo, porque en ese caso el campo es tangente al plano de la espira y no puede atravesar su superficie.
En cambio si B y n están paralelos, significa que el campo es perpendicular al plano de la espira y las líneas la atraviesan al máximo.
La unidad en Sistema Internacional para F es el weber (W), donde 1 W = 1 T.m2 (se lee “tesla por metro cuadrado”).
En la figura 1 podemos ver que la polaridad del voltaje cambia según se mueve el imán. La polaridad se establece mediante la ley de Lenz, la cual afirma que el voltaje inducido debe oponerse a la variación que lo produce.
Si por ejemplo el flujo magnético producido por el imán aumenta, en el conductor se establece una corriente que circula creando un flujo propio, que se opone a este aumento.
Si por el contrario el flujo creado por el imán disminuye, la corriente inducida circula de forma tal que el flujo propio contrarreste dicha disminución.
Para tomar en cuenta este fenómeno, se antepone un signo negativo a la ley de Faraday y ya no es necesario colocar las barras de valor absoluto:
ε = -ΔΦ/Δt
Esta es la ley de Faraday-Lenz. Si la variación del flujo es infinitesimal, se sustituyen las deltas por diferenciales:
ε = -dΦ/dt
La ecuación anterior es válida para una espira. Pero si tenemos una bobina de N vueltas, el resultado es mucho mejor, porque la fem se multiplica N veces:
ε = – N(dΦ/dt)
Para que se produzca la corriente que enciende el bombillo, entre el imán y la espira debe existir un movimiento relativo. Esta es una de las formas en que el flujo puede variar, porque de esta forma cambia la intensidad del campo que atraviesa la espira.
En el instante en que cesa el movimiento del imán, el bombillo se apaga, incluso si el imán se deja quieto en medio de la espira. Lo que se necesita para que circule la corriente que prenda al bombillo es que el flujo de campo varíe.
Cuando el campo magnético varía con el tiempo, lo podemos expresar como:
B = B (t).
Al mantener constante el área A de la espira y dejándola fija a un ángulo constante, que en el caso de la figura es 0º, entonces:
Si se consigue cambiar el área de la espira, dejando fija su orientación y poniéndola en medio de un campo constante, la fem inducida viene dada por:
Una manera de lograrlo es poner una barra que deslice sobre un riel conductor a cierta velocidad, como se muestra en la siguiente figura.
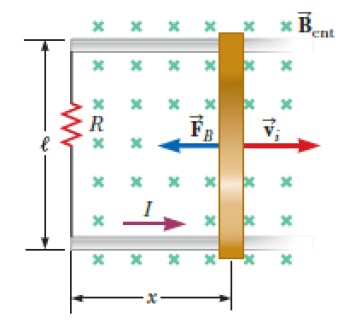
La barra y el riel, más un bombillo o una resistencia conectada con alambre conductores, forman un circuito cerrado en forma de espira rectangular.
Al deslizar la barra, la longitud x aumenta o disminuye, y con ello el área de la espira cambia, lo cual es suficiente para crear un flujo variable.
Como dijimos antes, si el ángulo entre B y la normal de la espira se hace variar, el flujo de campo cambia de acuerdo a:
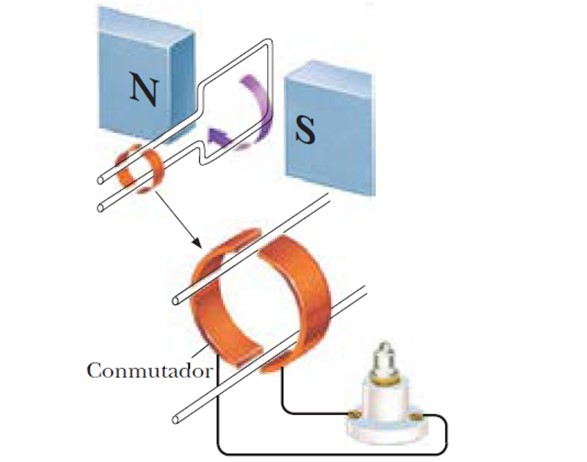
Se obtiene así un generador sinusoidal, y si en vez de una sola bobina se emplea un número N de bobinas, la fem inducida es mayor:
Una bobina circular de N vueltas y radio R, gira con frecuencia angular ω en medio de un campo magnético de magnitud B. Encontrar una expresión para la fem máxima inducida en la bobina.
Solución
Se aplica la expresión para la fem inducida por rotación cuando la bobina tiene N vueltas, sabiendo que:
-El área de la bobina es A = πR2
-El ángulo θ varía en función del tiempo como θ= ωt
Es importante tomar en cuenta que primero se sustituye θ= ωt en la ley de Faraday y luego se deriva respecto al tiempo:
ε = -NBA (cos θ)’ = -NB(πR2).[cos (ωt)]’ = NBω(πR2)sen(ωt)
Puesto que se pide la fem máxima, esta ocurre siempre que sen ωt = 1, por lo que finalmente:
εmáx = NBω(πR2)
- Figueroa, D. 2005. Serie: Física para Ciencias e Ingeniería. Volumen 6. Electromagnetismo. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. Second Edition. McGraw Hill.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed. Prentice Hall.
- Resnick, R. 1999. Física. Vol. 2. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 2.
