Interferencia destructiva: fórmula y ecuaciones, ejemplos, ejercicio
La interferencia destructiva, en física, se da cuando dos ondas independientes que se combinan en una misma región del espacio están desfasadas. Entonces las crestas de una de las ondas se encuentra con los valles de la otra y el resultado es una onda con amplitud nula.
Varias ondas pasan sin problema por un mismo punto del espacio y después cada una sigue su camino sin ser afectadas, como las ondas en el agua de la siguiente figura:

Supongamos dos ondas de igual amplitud A y frecuencia ω, a las que llamaremos y1 y y2, que se pueden describir matemáticamente mediante las ecuaciones:
y1= A sen (kx-ωt)
y2 = A sen (kx-ωt + φ)
La segunda onda y2 tiene un desfase φ respecto a la primera. Cuando se combinan, ya que las ondas se pueden superponer sin problemas, dan lugar a una onda resultante llamada yR:
yR = y1 + y2 = A sen (kx-ωt) + A sen (kx-ωt + φ)
Mediante la identidad trigonométrica:
sen α + sen β = 2 sen (α+ β)/2 . cos (α – β)/2
La ecuación para yR se transforma en:
yR = [2A cos (φ/2)] sen (kx – ωt + φ/2)
Ahora bien, esta nueva onda tiene una amplitud resultante AR = 2A cos (φ/2), que depende de la diferencia de fase. Cuando esta diferencia de fase adquiere los valores +π o –π, la amplitud resultante es:
AR = 2A cos (± π/2) = 0
Puesto que cos (± π/2) = 0. Precisamente entonces es cuando ocurre la interferencia destructiva entre las ondas. En general, si el argumento del coseno es de la forma ± kπ/2 con k impar, la amplitud AR es 0.
Índice del artículo
Como hemos visto, cuando dos o más ondas pasan al mismo tiempo por un punto, se superponen, dando lugar a una onda resultante cuya amplitud depende de la diferencia de fase entre las participantes.
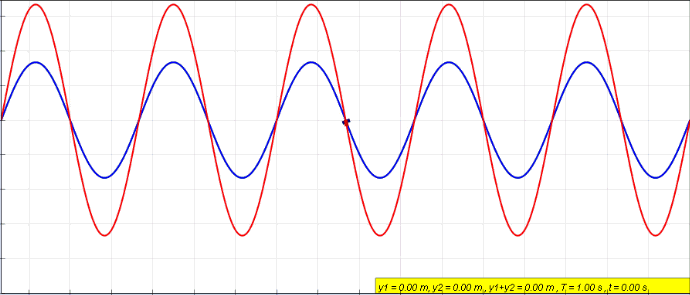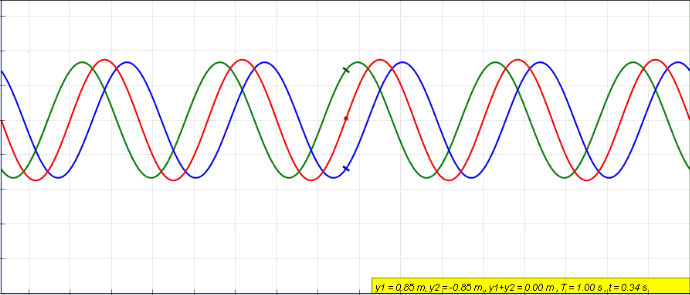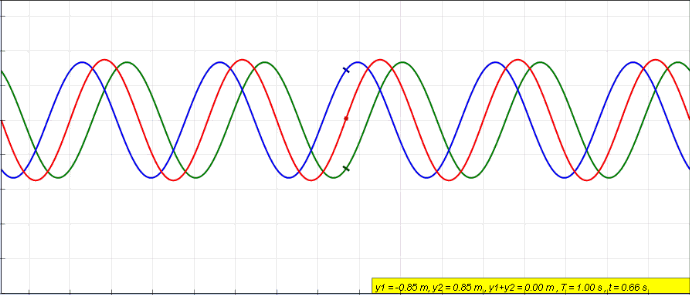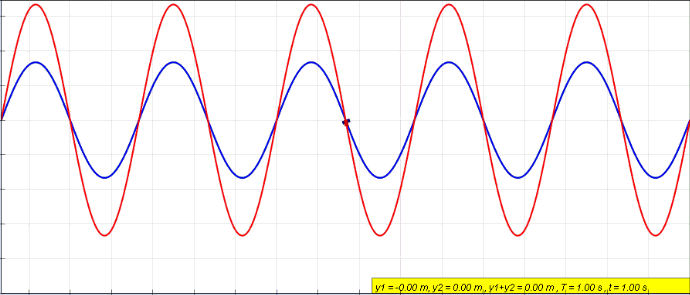
La onda resultante tiene la misma frecuencia y número de onda que las ondas originales. En la siguiente animación se superponen dos ondas en colores azul y verde. La onda resultante está en color rojo.
La amplitud crece cuando la interferencia es constructiva, pero se anula cuando es destructiva.
A las ondas que tienen la misma amplitud y frecuencia se las llama ondas coherentes, siempre y cuando mantengan fija entre ellas la misma diferencia de fase φ. Un ejemplo de onda coherente es la luz del láser.
Cuando las ondas azul y verde están desfasadas en 180 º en un punto dado (ver la figura 2), significa que mientras se desplazan, tienen diferencias de fase φ de π radianes, 3π radianes, 5π radianes y así sucesivamente.
De esta forma, al dividir el argumento de la amplitud resultante entre 2, resulta (π/2) radianes, (3π/2) radianes… Y el coseno de tales ángulos siempre es 0. Por lo tanto la interferencia es destructiva y la amplitud se hace 0.
Supongamos que dos ondas coherentes comienzan en fase una con la otra. Tales ondas pueden ser las que se propagan por el agua gracias a dos barras que vibran. Si las dos ondas viajan hasta un mismo punto P, recorriendo distancias diferentes, la diferencia de fase es proporcional a la diferencia de camino.
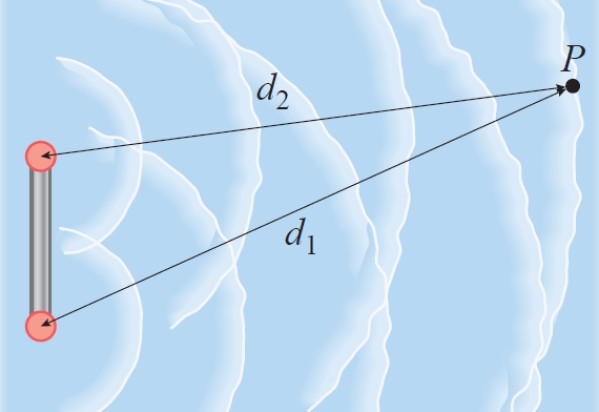
Como una longitud de onda λ equivale a una diferencia de 2π radianes, entonces se cumple que:
│d1 – d2│/ λ = diferencia de fase / 2π radianes
Diferencia de fase = 2π x│d1 – d2│/ λ
Si la diferencia de caminos es un número impar de semi-longitudes de onda, es decir: λ/2, 3λ/2, 5λ/2 y así sucesivamente, entonces la interferencia es destructiva.
Pero si la diferencia de caminos es un número par de longitudes de onda, la interferencia es constructiva y las amplitudes se suman en el punto P.
Las ondas de luz también pueden interferir entre ellas, tal como puso de manifiesto Thomas Young en 1801 a través de su celebrado experimento de la doble rendija.
Young hizo pasar luz a través de una rendija hecha sobre una pantalla opaca, la cual de acuerdo al principio de Huygens, genera a su vez dos fuentes de luz secundarias. Dichas fuentes siguieron su camino a través de una segunda pantalla opaca con dos rendijas y la luz resultante se proyectó sobre una pared.
El diagrama se observa en la siguiente imagen:
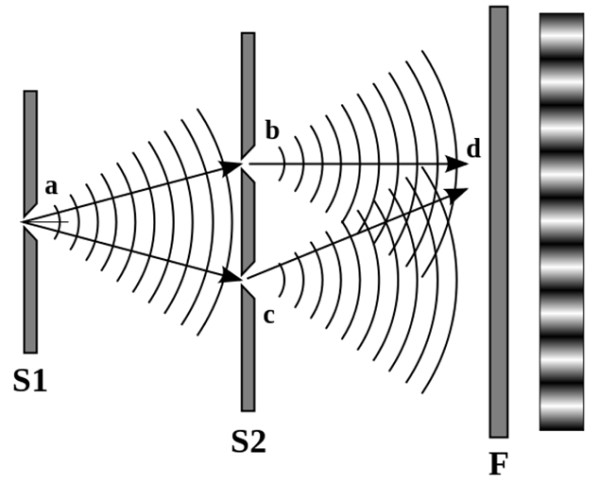
Young observó un patrón distintivo de líneas claras y oscuras alternadas. Cuando las fuentes de luz interfieren destructivamente, las líneas son oscuras, pero si lo hacen constructivamente, las líneas son claras.
Otro ejemplo interesante de interferencia son las pompas de jabón. Estas son películas muy delgadas, en las cuales la interferencia se produce porque la luz se refleja y se refracta en las superficies que limitan la película de jabón, tanto por encima como por debajo.

Como el espesor de la película es comparable a la longitud de onda, la luz se comporta al igual que lo hace cuando pasa por las dos rendijas de Young. El resultado es un patrón de colores si la luz incidente es blanca.
Se debe a que la luz blanca no es monocromática, sino que contiene todas las longitudes de onda (frecuencias) del espectro visible. Y cada longitud de onda se ve como un color distinto.
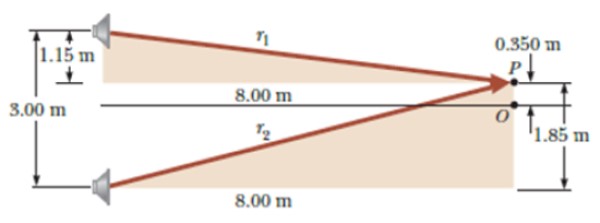
Dos parlantes idénticos accionados por el mismo oscilador están separados 3 metros y un oyente está a 6 metros de distancia del punto medio de separación entre los parlantes, en el punto O.
Luego se traslada al punto P, a una distancia perpendicular de 0.350 del punto O, tal como se muestra en la figura. Allí deja de escuchar el sonido por primera vez. ¿Cuál es la longitud de onda en la cual emite el oscilador?
Solución
La amplitud de la onda resultante es 0, por lo tanto la interferencia es destructiva. Se tiene que:
Diferencia de fase = 2π x│r1 – r2│/ λ
Por el teorema de Pitágoras aplicado a los triángulos sombreados de la figura:
r1 = √1.152 + 82 m = 8.08 m; r2 = √1.852 + 82 m = 8.21 m
│r1 – r2│= │8.08 – 8.21 │ m = 0.13 m
Los mínimos ocurren en λ/2, 3λ/2, 5λ/2 … El primero corresponde a λ/2, entonces, de la fórmula para la diferencia de fase se tiene:
λ = 2π x│r1 – r2│/ Diferencia de fase
Pero la diferencia de fase entre las ondas debe ser π, para que la amplitud AR = 2A cos (φ/2) sea nula, entonces:
λ = 2π x│r1 – r2│/ π = 2 x 0.13 m = 0.26 m
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 7. Ondas y Física Cuántica. Editado por Douglas Figueroa (USB).
- Fisicalab. Interferencia de ondas. Recuperado de: fisicalab.com.
- Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
- Serway, R. Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Wikipedia. Interferencia en láminas delgadas. Fuente: es.wikipedia.org.
