Puntos coplanares: ecuación, ejemplo y ejercicios resueltos
Los puntos coplanares pertenecen todos a un mismo plano. Dos puntos siempre son coplanares, ya que dichos puntos definen una recta por la cual pasan infinitos planos. Entonces, ambos puntos pertenecen a cada uno de los planos que pasan por la recta y por tanto, siempre serán coplanares.
Por otra parte, tres puntos definen un único plano, de lo cual se sigue que tres puntos siempre serán coplanares al plano que ellos determinan.
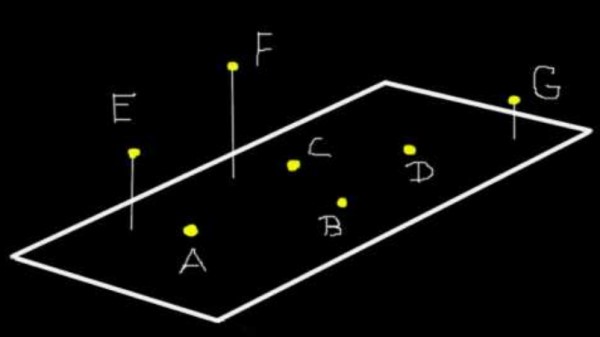
Más de tres puntos pueden ser coplanares o no. Por ejemplo en la figura 1, los puntos A, B, C y D son coplanares al plano (Ω). Pero E, F y G no son coplanares a (Ω), aunque sí son coplanares al plano que ellos tres definen.
Índice del artículo
La ecuación de un plano determinado por tres puntos conocidos A, B, C es una relación matemática que garantiza que cualquier punto P de coordenadas genéricas (x, y, z) que cumpla la ecuación pertenece a dicho plano.
La afirmación anterior es equivalente a decir que si P de coordenadas (x, y, z) cumple la ecuación del plano, entonces dicho punto será coplanar con los tres puntos A, B, C que determinaron el plano.
Para hallar la ecuación de dicho plano comencemos por encontrar los vectores AB y AC:
AB = [ Bx – Ax, By – Ay, Bz – Az ]
AC = [ Cx – Ax, Cy – Ay, Cz – Az ]
El producto vectorial AB X AC da como resultado un vector perpendicular o normal al plano determinado por los puntos A, B, C.
Un punto P cualquiera de coordenadas (x, y, z) pertenece al plano si se cumple que el vector AP es perpendicular al vector AB X AC, lo cual queda garantizado si se cumple:
AP • (AB X AC) = 0
Esto es equivalente a decir que el producto triple de AP, AB y AC sea nulo. La ecuación anterior puede escribirse en forma matricial:
Sean los puntos A(0, 1, 2); B(1, 2, 3); C(7, 2, 1) y D(a, 0, 1). ¿Qué valor debe tener a para que los cuatro puntos sean coplanares?
Para encontrar el valor de a es necesario que el punto D sea parte del plano determinado por A, B y C, lo cual se garantiza si cumple la ecuación del plano.
Desarrollando el determinante tenemos:
a(-1-1) + 1(-1 – 7) -1(1 – 7) = -2a -8 + 6 = -2a – 2 = 0
La ecuación anterior nos indica que a = -1 para que se cumpla la igualdad. En otras palabras, la única manera que el punto D(a, 0,1) sea coplanar con los puntos A, B y C es que a valga -1. De lo contrario no será coplanar.
Un plano intersecta a los ejes cartesianos X, Y, Z en 1, 2 y 3 respectivamente. La intersección de dicho plano con los ejes determina los puntos A, B y C. Encontrar la componente Dz de un punto D, cuyas componentes cartesianas son:
D(-Dz, Dz+1, Dz)
A condición de que D sea coplanar con los puntos A, B y C.
Solución
Cuando se conocen las intercepciones de un plano con los ejes cartesianos, puede usarse la forma segmentaria de la ecuación del plano:
x/1 + y/2 + z/3 = 1
Como el punto D debe pertenecer al plano anterior, se tiene que:
-Dz/1 + (Dz+1)/2 + Dz/3 = 1
Es decir:
-Dz + Dz/2 +½ + Dz/3 = 1
Dz(-1 + ½ + ⅓ ) = ½
Dz (-1/6⅙) = ½
Dz = -3
De lo anterior se desprende que el punto D(3, -2, -3) es coplanar con los puntos A(1, 0, 0); B(0, 2, 0) y C(0, 0, 3).
Determine si los puntos A(0, 5, 3); B(0, 6, 4); C(2, 4, 2) y D(2, 3, 1) son coplanares.
Solución
Formamos la matriz cuyas filas son las coordenadas de D-A, B-A, y C-A. Luego se calcula el determinante y se verifica si es o no cero.
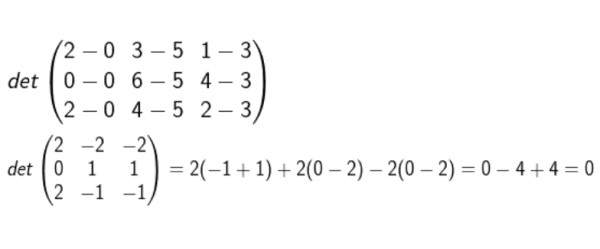
Después de efectuar todos los cálculos, se concluye que sí son coplanares.
Se dan dos rectas en el espacio. Una de ellas es la recta (R) cuya ecuación paramétrica es:
(R): x = 1 + 2 λ ; y = 1 – λ; z = 1
Y la otra es la recta (S) cuya ecuación es:
(S): x + 2 y = 1 ; z = -1
Demostrar que (R) y (S) son rectas coplanarias, es decir, se encuentran en un mismo plano.
Solución
Comencemos tomando arbitrariamente dos puntos en la recta (R) y dos en la recta (S):
Recta (R): λ=0; A(1, 1, 1) y λ=1; B(3, 0, 1)
Hagamos x= 0 sobre la recta (S)=> y = ½; C(0, ½, -1). Y por otra parte, si hacemos y= 0 =>x= 1; D(1, 0, -1).
Es decir, hemos tomado los puntos A y B que pertenecen a la recta (R) y los puntos C y D que pertenecen a la recta (S). Si esos puntos son coplanares, entonces las dos rectas también lo serán.
Ahora elegimos al punto A como el pivote y después encontramos las coordenadas de los vectores AB, AC y AD. De esta forma se obtiene:
B – A : (3-1, 0 -1, 1 – 1) =>AB= (2, -1, 0)
C – A: (0-1, 1/2 -1, -1 – 1) =>AC= (-1, -1/2, -2)
D – A: (1-1, 0 -1, -1 – 1) =>AD= (0, -1, -2)
El próximo paso es construir y calcular el determinante cuya primera fila son los coeficientes del vector AB, la segunda fila son los de AC y la tercera fila los del vector AD:
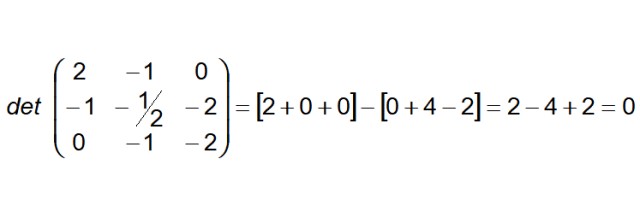
Como el determinante resulta ser nulo, entonces podemos concluir que los cuatro puntos son coplanarios. Adicionalmente puede afirmarse que las rectas (R) y (S) son también coplanares.
Las rectas (R) y (S) son coplanares, como se demostró en el ejercicio 3. Halle la ecuación del plano que las contiene.
Solución
Los puntos A, B, C definen completamente ese plano, pero queremos imponer que cualquier punto X de coordenadas (x, y, z) pertenezca al mismo.
X – A: (x-1, y -1, z – 1) =>AX= (x-1, y -1, z – 1)
B – A : (3-1, 0 -1, 1 – 1) =>AB= (2, -1, 0)
C – A: (0-1, 1/2 -1, -1 – 1) =>AC= (-1, -1/2, -2)
Para que X pertenezca al plano definido por A, B, C y en el que están contenidas las rectas (R) y (S), es necesario que se anule el determinante formado en su primera fila por las componentes de AX, en la segunda por las de AB y en la tercera por las de AC:

Siguiendo este resultado, agrupamos de esta forma:
2(x-1) + 4(y-1) -2(z-1) = 0
Y de inmediato se ve que puede ser reescrito así:
x – 1 + 2y – 2 – z + 1 = 0
Por lo tanto x + 2y – z = 2 es la ecuación del plano que contiene a las rectas (R) y (S).
- Fleming, W. 1989. Precalculus Mathematics. Prentice Hall PTR.
- Kolman, B. 2006. Álgebra lineal. Pearson Educación.
- Leal, J. M. 2005. Geometría Analítica Plana. Mérida – Venezuela: Editorial Venezolana C. A.
- Navarro, Rocio. Los vectores. Recobrado de: books.google.co.ve.
- Pérez, C. D. 2006. Precálculo. Pearson Educación.
- Prenowitz, W. 2012. Basic Concepts of Geometry. Rowman & Littlefield.
- Sullivan, M. 1997. Precálculo. Pearson Educación.
