Distribuciones discretas: definición, ejemplos, ejercicios resueltos
¿Qué es una distribución discreta?
Una distribución discreta de probabilidades es una función f(xi) que asigna a cada valor de una variable discreta: x1, x2, x3, … xi, una probabilidad de ocurrencia determinada P(X=xi). Dicha función se conoce también como “función masa de probabilidad”.
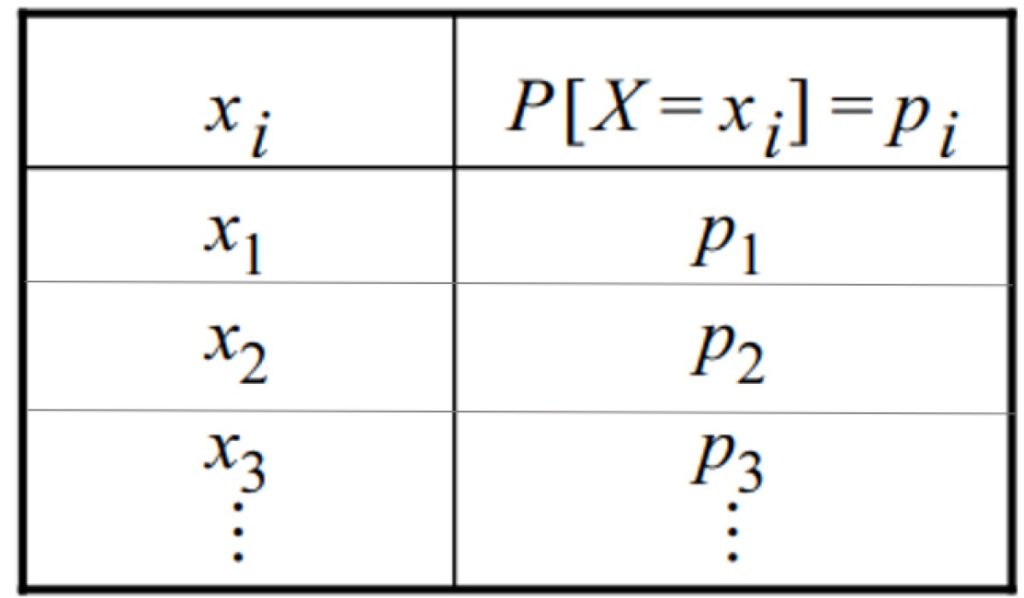
La distribución de probabilidad discreta se puede dar en forma de tabla o de gráfica. Una tabla tiene esta forma general, en la que aparece la variable en una columna y su respectiva probabilidad en la otra:
Las funciones de masa de probabilidad comparten las siguientes características generales:
- La probabilidad pi de un evento cualquiera xi está comprendida entre 0 y 1, pudiendo ser incluso alguno de estos valores límite: 0 ≤ x ≤ 1.
- P(X=xi) = pi solo toma valores positivos, por lo tanto: P(X=xi) ≥ 0.
- Se cumple que ∑ P(xi) = 1 para todos los valores posibles de x.
Una distribución de probabilidades describe el comportamiento de una población, descrita mediante sus parámetros: la media μ, la varianza σ2 y la desviación estándar S = √ σ2.
A continuación, se describen brevemente las distribuciones discretas más notables:
Distribución uniforme
Es la distribución discreta más simple de todas. En ella la variable puede tomar “n” valores discretos: x1, x2, x3, … xi, todos con la misma probablidad. En tal caso, la distribución viene dada por:
Distribución binomial
Se aplica a experiencias con solo dos resultados posibles y mutuamente excluyentes, a los cuales se les suele llamar “éxito” y “fracaso”, denotadas como E y F respectivamente. El hecho de que a un evento se le llame “éxito”, no necesariamente significa que sea algo bueno, es más bien una designación arbitraria.
A la probabilidad de éxito P(E) en “n” ensayos, se la denota como p, y a la de fracaso P(F) como q = 1 – p.
Si “x” representa un determinado número de éxitos en los “n” ensayos independientes, se cumple que: 0 ≤ x ≤ n. Y la probabilidad de ocurrencia P(x) del evento, se calcula a través de la siguiente fórmula:
Donde x = 0, 1, 2, 3…, n y el símbolo (!) significa “factorial”:
x! = x∙(x−1)∙(x−2) ∙(x−3)… 1
0! = 1
Distribución de Poisson
En esta distribución, la variable aleatoria x señala cuántas veces ocurre un evento en algún intervalo, que puede ser de tiempo, distancia u otro. Las ocurrencias del evento son aleatorias, independientes y están distribuidas de manera uniforme a lo largo del intervalo en cuestión.
Cumplidas estas condiciones, la probabilidad, que depende del promedio de ocurrencias μ y del número de Euler o número “e”, se calcula mediante:
Las probabilidades de que sucedan eventos con esta distribución son pequeñas, por eso se la denomina la “ley de los casos raros”.
Aproximación de la distribución binomial
La distribución de Poisson sirve como aproximación a la distribución binomial cuando n es grande (n≥ 100) y p es pequeña (np ≤ 10). En tal caso, la media μ se calcula como:
μ = n∙p
Distribución hipergeométrica
Se utiliza cuando las probabilidades no son independientes, es decir que, luego de llevar a cabo el experimento, las condiciones no vuelven a ser las mismas. Esto es lo que sucede al extraer muestras sin reemplazo de una población, por lo que ya no puede usarse la distribución binomial.
Si la población consta de dos tipos de objetos diferentes A y B, y se seleccionan n objetos al azar y sin reemplazo, la probabilidad de obtener x objetos del tipo A es:
Donde A y B son las cantidades respectivas de objetos de cada tipo, presentes en la población.
No obstante, si la población tiene un tamaño muy grande, aun si no hay reemplazo, es difícil que un mismo elemento pueda ser seleccionado más de una vez, por lo que ambas distribuciones: binomial e hipergeométrica, producen resultados similares.
Ejemplos
Lanzamientos de monedas
Los lanzamientos de monedas son ejemplos muy ilustrativos:
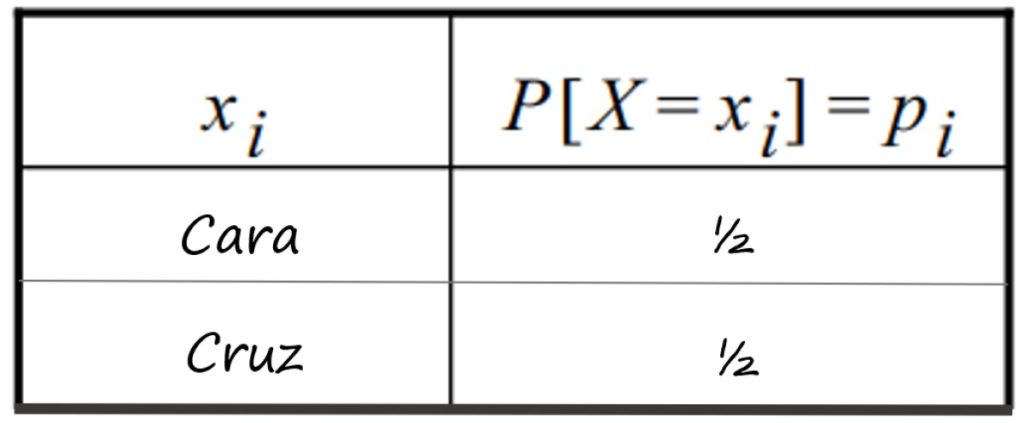
-El lanzamiento de una moneda honesta, y obtener una cara. Se sabe que 1 cara tiene ½ de probabilidad de salir y la cruz (0 cara), otro tanto. La distribución se muestra en esta tabla:
-El tiro simultáneo de dos monedas honradas y los posibles números de caras que se pueden obtener.

Variables con distribución uniforme
-La selección de un número entero que sea par o impar: cada uno tiene probabilidad igual a ½ de ser escogido dentro del conjunto de números enteros.
-El lanzamiento de un dado honesto. En este caso hay 6 caras numeradas y cada una tiene la misma probabilidad de salir: 1/6.
-La selección de un tema para hacer un examen, escogido de entre N temas, si todos ellos son igualmente probables.
Variables con distribución binomial
-Número de caras que salen al lanzar N veces una moneda honesta.
-De una población de 250 familias, el número de estas que tienen 2 hijos.
-La cantidad de rosales que sobreviven, luego de que un jardinero planta 20 rosales en un jardín.
-De un estudio con 50 pacientes, la cantidad de ellos que presentó una reacción negativa a un fármaco.
-La cantidad de estudiantes aprobados en un examen de Probabilidades, de un grupo conformado por 100 alumnos.
Variables con distribución de Poisson
-Número de llamadas por minuto al call center de una compañía.
-Cantidad de grandes terremotos al año para una zona geográfica concreta.
-El número de tornados que afectó a cierta región durante el último año.
-Cantidad de árboles infectados con un hongo, por hectárea cuadrada de bosque.
Variables con distribución hipergeométrica
-Aciertos de números o combinaciones ganadoras en juegos de azar.
-Selección de un determinado número de hembras o machos en una muestra de N peces de una pecera.
Ejercicios resueltos
Ejercicio 1
Un estudio determinó que al seleccionar al azar adultos que poseen teléfonos inteligentes, el 54% de ellos los usa estando en clase o en reuniones. Se quiere encontrar la probabilidad de que, seleccionando al azar 8 personas con teléfono inteligente, exactamente 6 de ellas los utilicen en clase o reuniones.
Solución
Este experimento concuerda con un experimento binomial, ya que el resultado es binario: una persona saca el teléfono en clase o no lo saca. Se puede llamar éxito al hecho de que la persona utiliza el teléfono estando en clase, y un fracaso si no lo hace (antes se explicó que esta elección es completamente arbitraria).
En ese caso: p = 0.54 y q = 1– 0.54 = 0.46.
Ya que se seleccionan al azar 8 personas, entonces n = 8 y el valor de x es 6, por lo tanto, se tienen los valores necesarios para sustituirlos en la fórmula de la distribución binomial:
Ejercicio 2
Durante un año reciente, una clínica registró 4221 nacimientos. Con este dato único, determinar la probabilidad de que haya 15 nacimientos en 1 día. ¿Es poco frecuente este suceso?
Solución
Se usa la distribución de Poisson, pues se pide determinar la probabilidad de ocurrencia de un evento que se produce en un intervalo de tiempo. En este caso, la variable es la cantidad de nacimientos y el intervalo es de 1 día.
La fórmula de la distribución de Poisson necesita del promedio de nacimientos por día, que se calcula fácilmente:
Por lo tanto, la probabilidad de x = 15 nacimientos/día es:
El resultado se puede expresar en términos de porcentaje para mayor claridad: 6.42% de probabilidades de que, en un día cualquiera, se produzcan exactamente 15 nacimientos. El evento es poco probable, aunque en ningún caso imposible.
