Diferencia entre segmento de recta y semirrecta (con ejemplos)

Un segmento de recta y una semirrecta se diferencian en que el segmento de recta está acotado; es decir, se conocen su punto inicial y su punto final. De la semirrecta se conoce su punto inicial, pero no su punto final, ya que se extiende hasta infinito.

En la siguiente figura se muestra, a la izquierda, un segmento de recta, y a la derecha, una semirrecta:

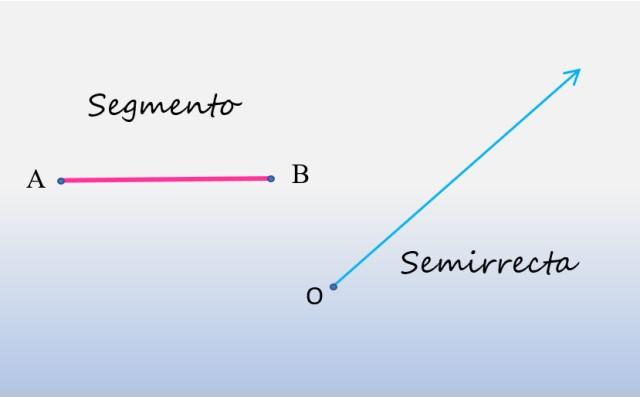
Como se puede apreciar, el segmento es una porción de recta, que comienza en el punto A y termina en el punto B, siendo estos puntos los extremos de dicho segmento. La medida del segmento corresponde a la longitud que existe entre sus extremos.

Por su parte, la semirrecta tiene su punto de partida en el punto O y se extiende hasta el infinito, lo que equivale a decir que está limitada solo por un extremo, usualmente llamado origen. Por este motivo se las llama también rayos.

Los segmentos se denotan mediante las letras que señalan el punto inicial y el final. Por ejemplo, el segmento de la figura es el segmento AB, o bien se coloca un trazo encima, así:

Por su parte, una semirrecta se puede nombrar también con dos letras, una indicando el punto correspondiente al origen y otra letra adicional. Puede usarse asimismo una letra minúscula para representar el rayo o semirrecta, y también hay semirrectas con nombre propios, como se verá en los ejemplos más adelante.

Ejemplos de segmentos

Los segmentos son muy importantes en geometría, a continuación se tienen algunos de los más notables:

Lados de un polígono

Los polígonos son figuras planas y cerradas, cuyos lados son segmentos de recta no consecutivos. Por ejemplo, un triángulo tiene tres lados, un cuadrilátero tiene cuatro lados, un pentágono tiene cinco y así sucesivamente.

Diámetro de una circunferencia

Se define como aquel segmento que contiene dos puntos de la circunferencia y obligatoriamente pasa por el centro de la misma.

Cuerda de una circunferencia

Cuando un segmento que une dos puntos de la circunferencia no pasa por su centro, se le denomina cuerda.

Altura de un triángulo

Se define la altura de un triángulo como el segmento que va perpendicularmente desde uno de los lados del triángulo hasta el vértice opuesto. Si se conoce la medida de la base de un triángulo, llamada b y la altura del mismo, denotada como h, se calcula el área A del mismo a través de la conocida fórmula:

A = ½ b∙h

Ejemplos de semirrectas

Las semirrectas también son elementos muy importantes en la geometría. Algunas semirrectas muy conocidas son:

Los semiejes positivos

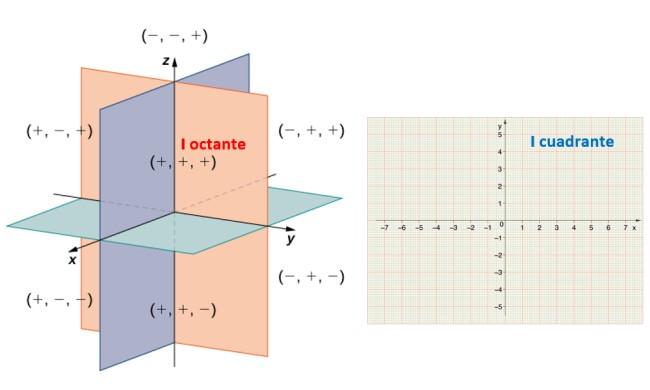
Las tres direcciones en el espacio: alto, ancho y profundidad, pueden representarse mediante un sistema de ejes cartesianos, consistente en tres rectas mutuamente perpendiculares entre sí, denotados como ejes x, y y z, que se cortan en un punto denominado origen.

Esta disposición divide al espacio en ocho regiones conocidas como octantes. En la siguiente figura se observan los semiejes positivos x, y y z, que determinan el primer octante. De igual manera, los semiejes positivos x y y, determinan la región del plano llamado primer cuadrante.

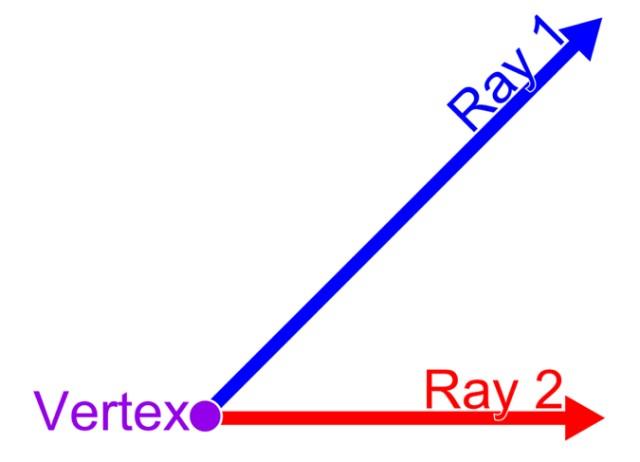
Los lados de un ángulo

Un ángulo es la fracción del plano que se encuentra delimitada por dos semirrectas cuyo origen es común. Este punto en común es el vértice del ángulo, mientras que las semirrectas se denominan, respectivamente, lado inicial y lado final del ángulo. Tal disposición se muestra en la siguiente figura: