¿Qué son las derivadas algebraicas? (Con ejemplos)

¿Qué son las derivadas algebraicas?

Las derivadas algebraicas consisten en el estudio de la derivada en el caso particular de funciones algebraicas. El origen de la noción de derivada se remonta a la Antigua Grecia. El desarrollo de esta noción estuvo motivada por la necesidad de resolver dos problemas importantes, uno en física y otro en matemáticas.

En física, la derivada resuelve el problema de determinar la velocidad instantánea de un objeto en movimiento. En matemáticas, permite hallar la recta tangente a una curva en un punto dado.

Aunque realmente son muchos más los problemas que se resuelven haciendo uso de la derivada, así como sus generalizaciones, resultados que vinieron posteriormente a la introducción de su concepto.

Los pioneros del cálculo diferencial son Newton y Leibniz. Antes de dar la definición formal, vamos a desarrollar la idea que hay detrás, desde el punto de vista matemático y físico.

La derivada como pendiente de la recta tangente a una curva

Supongamos que el gráfico de una función y=f(x) es un gráfico continuo (sin picos o vértices ni separaciones), y sea A=(a,f(a)) un punto fijo sobre él. Queremos hallar la ecuación de la recta tangente al gráfico de la función f en el punto A.

Tomemos otro punto cualquiera P=(x,f(x)) del gráfico, cercano al punto A, y tracemos la recta secante que pasa por A y por P. Una recta secante es una recta que corta al gráfico de una curva en uno o más puntos.

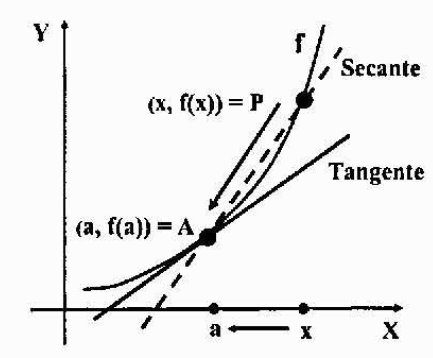
Para obtener la recta tangente que queremos, solo hace falta calcular la pendiente pues ya tenemos un punto de la recta: el punto A.

Si movemos el punto P por el gráfico y lo acercamos cada vez más al punto A, la recta secante anteriormente mencionada se aproximará a la recta tangente que se quiere hallar. Tomando el límite cuando “P tiende a A”, ambas rectas coincidirán, por lo tanto sus pendientes también.

La pendiente de la recta secante viene dada por

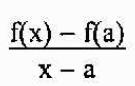
Decir que P se aproxima a A, es equivalente a decir que “x” se aproxima a “a”. Así, la pendiente de la recta tangente al gráfico de f en el punto A, será igual a:

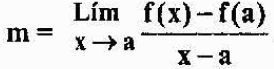
La expresión anterior se denota por f’(a), y se define como la derivada de una función f en el punto “a”. Vemos pues que analíticamente, la derivada de una función en un punto es un límite, pero geométricamente, es la pendiente de la recta tangente al gráfico de la función en el punto.

Ahora veremos esta noción desde el punto de vista de la física. Llegaremos a la misma expresión del límite anterior, aunque por un camino distinto, obteniendo así la unanimidad de la definición.

La derivada como velocidad instantánea de un objeto en movimiento

Veamos un breve ejemplo de lo que significa velocidad instantánea. Cuando se dice, por ejemplo, que un automóvil para llegar a un destino lo hizo con una velocidad de 100 km por hora, lo que significa es que en una hora recorrió 100 km.

Esto no significa necesariamente que durante toda la hora el automóvil siempre fue a 100 km, el velocímetro del automóvil pudo en algunos instantes marcar menos o más. Si tuvo la necesidad de pararse en un semáforo, la velocidad en ese instante fue de 0 km. Sin embargo, al cabo de una hora, el recorrido fue de 100 km.

Esto es lo que se conoce como velocidad promedio y viene dada por el cociente de la distancia recorrida entre el tiempo transcurrido, como acabamos de ver. La velocidad instantánea, por su parte, es la que marca la aguja del velocímetro de un automóvil en un instante (tiempo) determinado.

Veamos esto ahora d manera más general. Supongamos que un objeto se desplaza a lo largo de una recta y que este desplazamiento es representado por medio de la ecuación s=f(t), donde la variable t mide el tiempo y la variable s el desplazamiento, tomando en cuenta su inicio en el instante t=0, en cuyo momento también es cero, es decir, f(0)=0.

Esta función f(t) se conoce como función de posición.

Se busca una expresión para la velocidad instantánea del objeto en un instante fijo “a”. A esta velocidad la denotaremos por V(a).

Sea t un instante cualquiera cercano al instante “a”. En el intervalo de tiempo que hay entre “a” y “t”, el cambio de posición el objeto viene dado por f(t)-f(a).

La velocidad promedio en este intervalo de tiempo es:

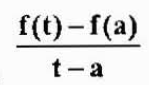
La cual es una aproximación de la velocidad instantánea V(a). Esta aproximación será mejor a medida que t se acerque más a “a”. Por lo tanto,

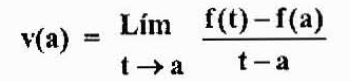
Observemos que esta expresión es igual a la obtenida en el caso anterior, pero desde una perspectiva diferente. Esto es lo que se conoce como la derivada de una función f en un punto “a” y se denota por f’(a), como se dijo anteriormente.

Notemos que haciendo el cambio h=x-a, se tiene que cuando “x” tiende a “a”, “h” tiende a 0, y el límite anterior se transforma (de manera equivalente) a:

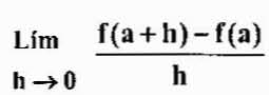
Ambas expresiones son equivalentes pero a veces conviene más utilizar una en lugar de la otra, dependiendo del caso.

Se define entonces de manera más general la derivada de una función f en un punto cualquiera “x” perteneciente a su dominio como

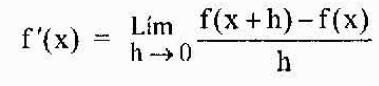
La notación más usual para representar la derivada de una función y=f(x) es la que acabamos de ver (f’ o y’). Sin embargo, otra notación muy usada es la notación de Leibniz que se representa como cualquiera de las siguientes expresiones:

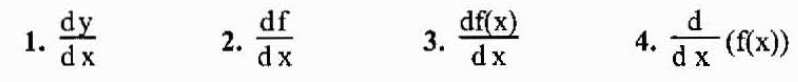
En vista de que la derivada es en esencia un límite, esta puede existir o no, pues los límites no siempre existen. En caso de que exista, se dice que la función en cuestión es diferenciable en el punto dado.

Función algebraica

Una función algebraica es una combinación de polinomios por medio de sumas, restas, productos, cocientes, potencias y radicales.

Un polinomio es una expresión de la forma

P_n=a_nxⁿ+ a_n-1x^n-1+ a_n-2x^n-2+…+ a₂x²+ a₁x+a₀

Donde n es un número natural y todos los a_i, con i=0,1,…,n, son números racionales y a_n≠0. En este caso se dice que el grado de este polinomio es n.

Los siguientes son ejemplos de funciones algebraicas:

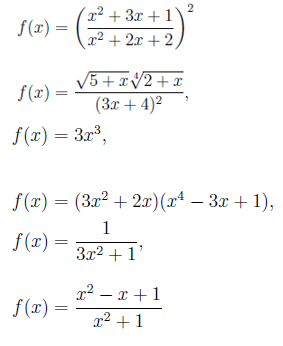
Aquí no están incluidas las funciones exponenciales, logarítmicas y trigonométricas. Las reglas de derivación que veremos a continuación son válidas para funciones en general, pero nos restringiremos y las aplicaremos en el caso de funciones algebraicas.

Reglas de derivación

Derivada de una constante

Establece que la derivada de una constante es cero. Es decir, si f(x)=c, entonces f’(x)=0. Por ejemplo, la derivada de la función constante 2 es igual a 0.

Derivada de una potencia

Si f(x)=xⁿ, entonces f’(x)=nx^n-1. Por ejemplo, la derivada de x³ es 3x². Como consecuencia de esto, se obtiene que la derivada de la función identidad f(x)=x es f’(x)=1x^1-1=x⁰=1.

Otro ejemplo es el siguiente: sea f(x)=1/x², entonces f(x)=x^-2 y f’(x)=-2x^-2-1=-2x^-3.

Esta propiedad también es válida raíces, pues las raíces son potencias racionales y se puede aplicar lo anterior también en ese caso. Por ejemplo, la derivada de una raíz cuadrada viene dada por

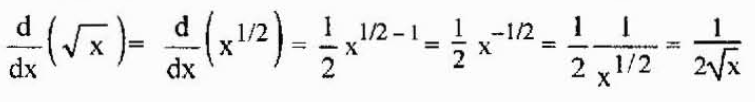
Derivada de una suma y de una resta

Si f y g son funciones diferenciables en x, entonces la suma f+g también lo es y se cumple que (f+g)’(x)=f’(x)+g’(x).

Análogamente se tiene que (f-g)’(x)=f’(x)-g’(x). En otras palabras, la derivada de una suma (resta), es la suma (o resta) de las derivadas.

Ejemplo

Si h(x)=x²+x-1, entonces

h’(x)=(x²)+(x)’-(1)’=2x+1-0=2x+1.

Derivada de un producto

Si f y g son funciones diferenciables en x, entonces el producto fg también es diferenciable en x y se cumple que

(fg)’(x)=f’(x)g(x)+f(x)g’(x).

Como consecuencia se tiene que si c es una constante y f es una función diferenciable en x, entonces cf también es diferenciable en x y (cf)’(x)=cf’(X).

Ejemplo

Si f(x)=3x(x²+1), entonces

f’(x)=(3x)’(x²+1)+(3x)(x²+1)’=3(x)’(x²+1)+3x[(x²)’+(1)’]

=3(1)( x²+1)+3x[(2x^2-1)+0]=3(x²+1)+3x(2x)=3x²+3+6x²

=9x²+3.

Derivada de un cociente

Si f y g son diferenciables en x y g(x)≠0, entonces f/g también es diferenciable en x, y se cumple que

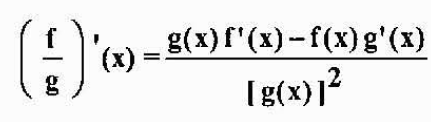
Ejemplo: si h(x)=x³/(x²-5x), entonces

h’(x)=[( x³)’(x⁵-5x)-( x³) (x⁵-5x)’]/ (x⁵-5x)²=[(3x²) (x⁵-5x)- ( x³) (5x⁴-5)]/ (x⁵-5x)².

Regla de la cadena

Esta regla permite derivar la composición de funciones. Establece lo siguiente: si y=f(u) es diferenciable en u, y u=g(x) es diferenciable en x, entonces la función compuesta f(g(x)) es diferenciable en x, y se cumple que [f(g(x))]’=f’(g(x))g’(x).

Es decir, la derivada de una función compuesta es el producto de la derivada de la función externa (derivada externa) por la derivada de la función interna (derivada interna).

Ejemplo

Si f(x)=(x⁴-2x)³, entonces

f’(x)=3(x⁴-2x)²(x⁴-2x)’=3(x⁴-2x)²(4x³-2).

También hay resultados para calcular la derivada de la inversa de una función, así como la generalización a derivadas de orden superior. Las aplicaciones son extensas. Entre ellas resaltan sus utilidades en problemas de optimización y de máximos y mínimos de funciones.

Referencias

1. Alarcon, S., González, M., & Quintana, H. (2008). Cálculo Diferencial. ITM.
2. Cabrera, V. M. (1997). Cálculo 4000. Editorial Progreso.
3. Castaño, H. F. (2005). Matemáticas previas al cálculo. Universidad De Medellin.
4. Eduardo, N. A. (2003). Introducción al Cálculo. Ediciones Umbral.
5. Fuentes, A. (2016). MATEMÁTICAS BÁSICAS. Una Introducción al Cálculo. Lulu.com.
6. Purcell, E. J., Rigdon, S. E., & Varberg, D. E. (2007). Cálculo. Pearson Educación.
7. Saenz, J. (2005). Cálculo Diferencial (Segunda ed.). Barquisimeto: Hipotenusa.
8. Thomas, G. B., & Weir, M. D. (2006). Cálculo: varias variables. Pearson Educación.