Análisis de mallas: conceptos, métodos, ejemplos
El análisis de mallas es una técnica empleada para resolver circuitos eléctricos planos. Este procedimiento también puede aparecer en la literatura con los nombres de método de las corrientes circuitales o método de las corrientes de malla (o lazo).
El fundamento de este y otros métodos de análisis de circuitos eléctricos está en las leyes de Kirchhoff y la ley de Ohm. Las leyes de Kirchhoff a su vez, son expresiones de dos principios importantísimos de conservación en la Física para sistemas aislados: tanto la carga eléctrica como la energía se conservan.

Por un lado, la carga eléctrica está relacionada con la corriente, que es carga en movimiento, mientras que en un circuito la energía está vinculada al voltaje, que es el agente encargado de hacer el trabajo necesario para que mantener la carga en movimiento.
Dichas leyes, aplicadas a un circuito plano, generan un conjunto de ecuaciones simultáneas que deben ser resueltas para obtener los valores de corriente o tensión.
El sistema de ecuaciones puede resolverse con técnicas analíticas ya conocidas, como la regla de Cramer, que requiere el cálculo de determinantes para obtener la solución del sistema.
Dependiendo del número de ecuaciones, se resuelven empleando una calculadora científica o un algún software matemático. En la red también hay muchas opciones disponibles.
Índice del artículo
Antes de explicar cómo funciona, comenzaremos por definir estos términos:
Rama: sección que contiene un elemento del circuito.
Nodo: punto que conecta dos o más ramas.
Lazo: es cualquier porción cerrada de un circuito, que comienza y termina en el mismo nodo.
Malla: lazo que no contiene ningún otro lazo en su interior (malla esencial).
El análisis de mallas es un método general que sirve para resolver circuitos cuyos elementos están conectados en serie, en paralelo o de forma mixta, es decir, cuando no se distingue claramente el tipo de conexión. El circuito debe ser plano, o al menos debe ser posible re-dibujarlo como tal.

En la figura de arriba se muestra un ejemplo de cada tipo de circuito. Una vez aclarado el punto, para comenzar, aplicaremos el método a un circuito sencillo como ejemplo en la siguiente sección, pero antes repasemos brevemente las leyes de Ohm y Kirchhoff.
Ley de Ohm: sean V el voltaje, R la resistencia e I la corriente del elemento resistivo óhmico, en el cual el voltaje y la corriente son directamente proporcionales, siendo la resistencia la constante de proporcionalidad:
V = I.R
Ley de Kirchhoff del voltaje (LKV): en cualquier trayectoria cerrada recorrida en una sola dirección, la suma algebraica de los voltajes es cero. Esto incluye los voltajes debidos a fuentes, resistores, inductores o capacitores: ∑ E = ∑ Ri. I
Ley de Kirchhoff de la corriente (LKC): en cualquier nodo, la suma algebraica de las corrientes es cero, teniendo en cuenta que a las corrientes que entran se les asigna un signo y a las que salen otro. De esta forma: ∑ I = 0.
Con el método de las corrientes de malla no es necesario aplicar la ley de las corrientes de Kirchhoff, resultando menos ecuaciones para resolver.
Comenzaremos explicando el método para un circuito de 2 mallas. El procedimiento se puede extender luego para circuitos más grandes.
Paso 1
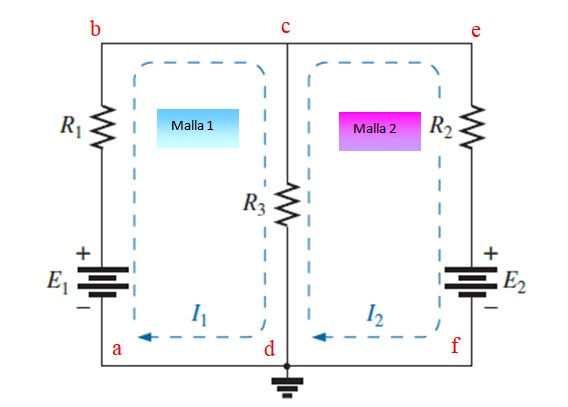
Asignar y dibujar corrientes independientes a cada malla, en este ejemplo son I1 e I2. Se pueden dibujar en sentido horario o también en sentido antihorario.
Paso 2
Aplicar la Ley de las Tensiones de Kirchhoff (LTK) y la ley de Ohm a cada malla. A las caídas de potencial se les asigna signo (-) mientras que a las subidas se les asigna signo (+).
Malla abcda
Partiendo del punto a y siguiendo el sentido de la corriente, encontramos una subida de potencial en el batería E1 (+), luego una caída en R1 (-) y después otra caída en R3 (-).
Simultáneamente, la resistencia R3 es atravesada también por la corriente I2, pero en sentido contrario, por lo tanto representa una subida (+). La primera ecuación queda así:
E1-R1.I1 –R3.I1 + R3.I2 = 0
Enseguida se factoriza y se reagrupan términos:
– (R1+R3)I1 +R3I2 = -E1 (Ecuación 1)
Malla cefdc
Partiendo del punto e y siguiendo el sentido de la corriente se encuentra una caída de potencial en R2 (-), otra caída en E2, ya que la corriente entra por el polo + de la batería y finalmente otra caída en R3 (-), Al mismo tiempo la corriente I1 atraviesa R3 en sentido contrario (+).
La segunda ecuación, con los signos indicados, queda de esta forma:
– R2 I2 – E2 –R3 I2 +R3 I1=0
R3I1 – (R2 +R3) I2 = E2 (Ecuación 2)
Nótese que se tienen dos ecuaciones con las dos incógnitas I1 e I2.
Paso 3
Seguidamente se resuelve el sistema de ecuaciones así formado.
Para comenzar, es importante tomar en cuenta lo siguiente:
-A las corrientes de lazo o corrientes de malla se les puede asignar una dirección arbitraria.
-A cada malla esencial –o “ventana”- que tenga el circuito debe asignársele una corriente.
-Las corrientes de malla se denotan con mayúscula para distinguirlas de las corrientes que circulan por ramas, aunque en algunos casos la corriente que circula por una rama puede la misma que la de malla.
Encontrar las corrientes que circulan por cada resistencia en el circuito de la figura 3, si los elementos tienen los siguientes valores:
R1 = 20 Ω; R2 = 30 Ω; R3 = 10 Ω; E1 = 12 V; E2 = 18 V
Solución
En primer lugar es preciso asignar las corrientes de malla I1 e I2 y tomar el sistema de ecuaciones según se dedujo en la sección precedente, después sustituir los valores dados en el enunciado:
– (R1+R3)I1 +R3I2 = -E1 (Ecuación 1)
R3I1 – (R2 +R3) I2 = E2 (Ecuación 2)
—————————
-(20+30) I1 + 10I2 = -12
10I1 – (30 +10)I2 = 18
————————-
-50I1 + 10I2 = -12
10I1 – 40 I2 = 18
Como se trata de un sistema de ecuaciones de 2 x 2, se puede resolver fácilmente por reducción, multiplicando por 5 la segunda ecuación para eliminar la incógnita I1:
-50I1 + 10 I2 = -12
50I1 – 200 I2 = 90
—————————
-190 I2=78
I2 = – 78/180 A = – 0.41 A
De inmediato se despeja la corriente I1 de cualquiera de las ecuaciones originales:
I1 = (18 + 40 I2) / 10 = (18 + 40 x (-0.41)) / 10 = 0.16 A
El signo negativo en la corriente I2 significa que la corriente en la malla 2 circula en sentido contrario al dibujado.
Las corrientes en cada resistencia son las siguientes:
Por la resistencia R1 circula la corriente I1 = 0.16 A en el sentido dibujado, por la resistencia R2 circula la corriente I2 = 0.41 A en sentido contrario al dibujado, y por la resistencia R3 circula i3 = 0.16- (-0.41) A = 0.57 A hacia abajo.
Solución del sistema por el método de Cramer
En forma matricial, el sistema puede ser resuelto de la siguiente manera:
Paso 1: Calcular Δ
Paso 2: Calcular Δ1
Se sustituye la primera columna por los términos independientes del sistema de ecuaciones, manteniendo el orden en que se planteó el sistema originalmente:
Paso 3: Calcular I1
I1 = Δ1/Δ = 300/1900 = 0.16 A
Paso 4: Calcular Δ2
I2 = Δ2/Δ = -780/1900 = -0.41 A
Determine la corriente y los voltajes a través de cada resistencia en el siguiente circuito, mediante el método de las corrientes de malla:
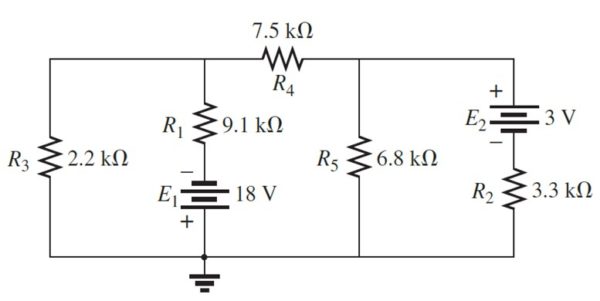
Solución
Se dibujan las tres corrientes de malla, tal como se muestra en la siguiente figura, en sentidos arbitrarios. Ahora se recorren las mallas partiendo desde cualquier punto:
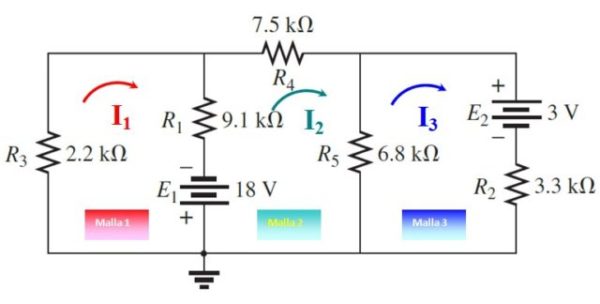
Malla 1
-9100.I1+18-2200.I1+9100.I2=0
-11300 I1 + 9100.I2 = -18
Malla 2
-(7500 +6800+9100) .I2 + 9100.I1+6800.I3-18 = 0
9100.I1 – 23400.I2 + 6800.I3 = 18
Malla 3
-(6800 + 3300) I3 + 6800.I2 – 3 =0
6800.I2 – 10100.I3 = 3
Sistema de ecuaciones
-11300 I1 + 9100.I2 + 0.I3= -18
9100.I1 – 23400.I2 + 6800.I3 = 18
0.I1 + 6800.I2 – 10100.I3 = 3
A pesar de que los números son grandes, se resuelve rápidamente con ayuda de una calculadora científica. Recuerde que las ecuaciones deben estar ordenadas y agregar ceros en los lugares donde la incógnita no aparezca, tal como aparece aquí.
Las corrientes de malla son:
I1 = 0.0012 A; I2 = -0.00048 A; I3 = -0.00062 A
Las corrientes I2 e I3 circulan en sentido contrario al mostrado en la figura, ya que resultaron ser negativas.
Tabla de corrientes y voltajes en cada resistencia
| Resistencia (Ω) | Corriente (Amperios) | Voltaje = I.R (Voltios) |
|---|---|---|
| 9100 | I1 –I2 = 0.0012–(-0.00048) = 0.00168 | 15.3 |
| 3300 | 0.00062 | 2.05 |
| 2200 | 0.0012 | 2.64 |
| 7500 | 0.00048 | 3.60 |
| 6800 | I2 –I3=-0.00048-(-0.00062)= 0.00014 | 0.95 |
Solución por regla de Cramer
Dado que son números grandes, es conveniente utilizar notación científica para trabajar con ellos en forma directa.
Cálculo de I1
Las flechas de colores en el determinante de 3 x 3 indican la forma de encontrar los valores numéricos, multiplicando los valores señalados. Comencemos por obtener los del primer corchete en el determinante Δ:

(-11300) x (-23400) x (-10100) = -2.67 x 1012
9100 x 0 x 0 = 0
9100 x 6800 x 0 = 0
De inmediato obtengamos el segundo corchete en ese mismo determinante, que se trabaja de izquierda a derecha (para este corchete no se dibujaron las flechas de colores en la figura). Invitamos al lector a que lo verifique:
0 x (-23400) x 0 = 0
9100 x 9100 x (-10100) = -8.364 x 1011
6800 x 6800 x (-11300) = -5.225 x 1011
Del mismo modo, el lector también puede verificar los valores para el determinante Δ1.
Importante: entre ambos corchetes siempre va un signo negativo.
Finalmente se obtiene la corriente I1 mediante I1 = Δ1 / Δ
I1 = -1.582 x 109/-1.31 x 1012 = 0.0012 A
Cálculo de I2
El procedimiento puede repetirse para calcular I2, en este caso, para calcular el determinante Δ2 se sustituye la segunda columna del determinante Δ por la columna de los términos independientes y se encuentra su valor, según el procedimiento explicado.
Sin embargo, como es engorroso a causa de los números grandes, sobre todo si no se dispone de calculadora científica, lo más sencillo es sustituir el valor de I1 ya calculado, en la siguiente ecuación y despejar:
-11300 I1 + 9100.I2 + 0.I3= -18 → 9100 I2= -18 + 11300 I1 → I2 = -0.00048 A
Cálculo de I3
Una vez con los valores de I1 e I2 en mano, el de I3 se encuentra directamente por sustitución.
- Alexander, C. 2006. Fundamentos de Circuitos Eléctricos. 3ra. Edición. Mc Graw Hill.
- Boylestad, R. 2011. Introducción al Análisis de Circuitos.2da. Edición. Pearson.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 5. Interacción Eléctrica. Editado por Douglas Figueroa (USB).
- García, L. 2014. Electromagnetismo. 2da. Edición. Universidad Industrial de Santander.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 2.
