Trapecio escaleno: propiedades, fórmulas y ecuaciones, ejemplos
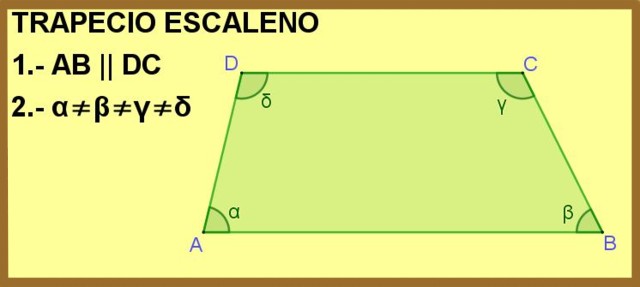
Un trapecio escaleno es un polígono de cuatro lados, dos de los cuales son paralelos entre sí, y con sus cuatro ángulos interiores de medidas distintas.
Seguidamente se muestra el cuadrilátero ABCD, donde los lados AB y DC son paralelos entre sí. Con esto basta para que sea un trapecio, pero además, los ángulos interiores α, β, γ y δ son todos diferentes, por tanto el trapecio es escaleno.
Índice del artículo
- 1 Elementos del trapecio escaleno
- 2 Propiedades
- 3 Fórmulas y ecuaciones
- 4 Construcción del trapecio escaleno con regla y compás
- 5 Ejemplo
- 6 Ejercicio resuelto
- 7 Referencias
A continuación los elementos más característicos:
-Bases y laterales: los lados paralelos del trapecio son sus bases y los dos lados no paralelos son los laterales.
En un trapecio escaleno las bases son de longitudes diferentes y las laterales también. Sin embargo, un trapecio escaleno puede tener una lateral de igual longitud que una base.
-Mediana: es el segmento que une los puntos medios de las laterales.
-Diagonales: la diagonal de un trapecio es el segmento que une dos vértices opuestos. Un trapecio, como todo cuadrilátero, tiene dos diagonales. En el trapecio escaleno son de diferente longitud.
Además del trapecio escaleno, existen otros trapecios particulares: el trapecio rectángulo y el trapecio isósceles.
Un trapecio es rectángulo cuando uno de sus ángulos es recto, mientras que trapecio isósceles tiene sus laterales de igual longitud.
La forma trapezoidal tiene numerosas aplicaciones a nivel de diseño e industria, como por ejemplo en la configuración de las alas de los aviones, la forma de objetos cotidianos como mesas, respaldos de sillas, envases, carteras, estampados textiles y más.
A continuación se enumeran las propiedades del trapecio escaleno, muchas de las cuales son extensivas a los otros tipos de trapecio. En lo que sigue, cuando se hable de “trapecio”, la propiedad será aplicable a cualquier tipo, incluyendo al escaleno.
1. La mediana del trapecio, es decir el segmento que une los puntos medios de sus lados no paralelos, es paralelo a cualquiera de las bases.
2.- La mediana de un trapecio tiene una longitud que es la semisuma de la de sus bases y corta a sus diagonales en el punto medio.
3.- Las diagonales de un trapecio se intersectan en un punto que las dividen en dos secciones que son proporcionales a los cocientes de las bases.
4.- La suma de los cuadrados de las diagonales de un trapecio es igual a la suma de los cuadrados de sus laterales más el doble producto de sus bases.
5.- El segmento que une los puntos medios de las diagonales tiene longitud igual a la semidiferencia de las bases.
6.- Los ángulos adyacentes a las laterales son suplementarios.
7.- En un trapecio escaleno la longitud de sus diagonales son diferentes.
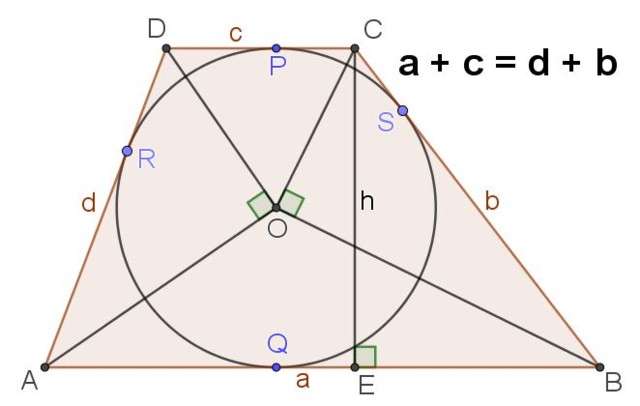
8.- Un trapecio tiene circunferencia inscrita solo si la suma de sus bases es igual a la suma de sus laterales.
9.- Si un trapecio tiene circunferencia inscrita, entonces el ángulo con vértice en el centro de dicha circunferencia y lados que pasan por los extremos de la lateral del trapecio es recto.
10.- Un trapecio escaleno no tiene circunferencia circunscrita, el único tipo de trapecio que si la tiene es el isósceles.
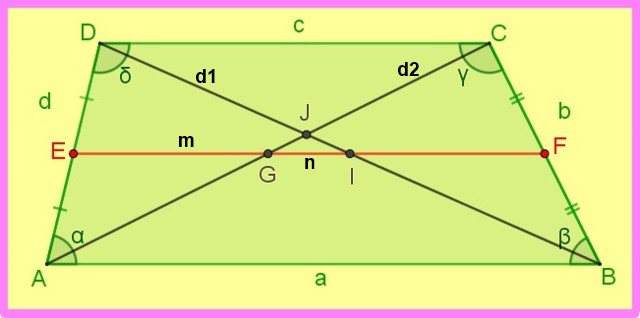
Las siguientes relaciones del trapecio escaleno están referidas a la siguiente figura.
1.- Si AE = ED y BF = FC → EF || AB y EF || DC.
2.- EF = (AB + DC)/2 es decir: m = (a + c)/2.
3.- DI = IB = d1 /2 y AG = GC = d2 /2.
4.- DJ / JB = (c / a) similarmente CJ / JA = (c / a).
5.- DB2 + AC2 = AD2 + BC2 + 2 AB∙DC
Equivalentemente:
d12 + d22 = d2 + b2 + 2 a∙c
6.- GI = (AB – DC)/2
Es decir:
n = ( a – c )/2
7.- α + δ = 180⁰ y β + γ = 180⁰
8.- Si α ≠ β ≠ γ ≠ δ entonces d1 ≠ d2.
9.- En la figura 4 se muestra un trapecio escaleno que tiene circunferencia inscrita, en ese caso se cumple que:
a + c = d + b
10.- En un trapecio escaleno ABCD con circunferencia inscrita de centro O también se cumple lo siguiente:
∡AOD = ∡BOC = 90⁰
Se define la altura de un trapecio como el segmento que va desde un punto de la base perpendicularmente hasta la base opuesta (o a su prolongación).
Todas las alturas del trapecio tienen la misma medida h, por lo que la mayoría de las veces la palabra altura se refiere a su medida. En síntesis, la altura es la distancia o separación entre las bases.
La altura h puede determinarse si se conoce la longitud de una lateral y uno de los ángulos adyacentes a la lateral:
h = d Sen(α) = d Sen(γ) = b Sen(β) = b Sen(δ)
La medida m de la mediana del trapecio es la semisuma de las bases:
m = (a + b)/2
d1 = √[a2 + d2 – 2∙a∙d∙Cos(α)]
d2= √[a2 + b2 – 2∙a∙b∙Cos(β)]
También puede calcularse si solo se conoce la longitud de los lados del trapecio:
d1 = √[b2 + a∙c – a(b2 – d2)/(a – c)]
d2 = √[d2 + a∙c – a(d2 – b2)/(a – c)]
El perímetro es la longitud total del contorno, es decir la suma de todos sus lados:
P = a + b + c + d
El área de un trapecio es la semisuma de sus bases multiplicada por su altura:
A = h∙(a + b)/2
También puede calcularse si se conoce la mediana m y la altura h:
A = m∙h
En caso que solo se conozca la longitud de los lados del trapecio, el área puede determinarse mediante la fórmula de Herón para el trapecio:
A = [(a+c)/|a–c|]∙√[(s-a)(s-c)(s-a-d)(s-a-b)]
Donde s es el semiperímetro: s = (a+b+c+d)/2.
El corte de la mediana con las diagonales y la paralela que pasa por la intersección de las diagonales, da lugar a otras relaciones.
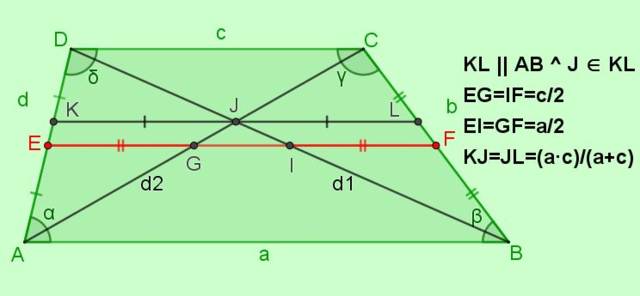
-Relaciones para la mediana EF
EF = (a+c)/2; EG = IF = c/2; EI = GF = a/2
-Relaciones para el segmento paralelo a las bases KL, y que pasa por el punto de intersección J de las diagonales
Si KL || AB || DC con J ∈ KL, entonces KJ = JL = (a∙c)/(a+c)
Dadas las bases de longitudes a y c, siendo a > c y con laterales de longitudes b y d, siendo b > d, se procede siguiendo estos pasos (ver figura 6):
1.- Con la regla se traza el segmento de la mayor AB.
2.- A partir de A se y sobre AB se marca el punto P de modo que AP = c.
3.- Con el compás con centro en P y radio d se traza un arco.
4.- Se hace centro en B con radio b trazando un arco que intercepte al arco trazado en el paso anterior. Llamamos Q al punto de intersección.
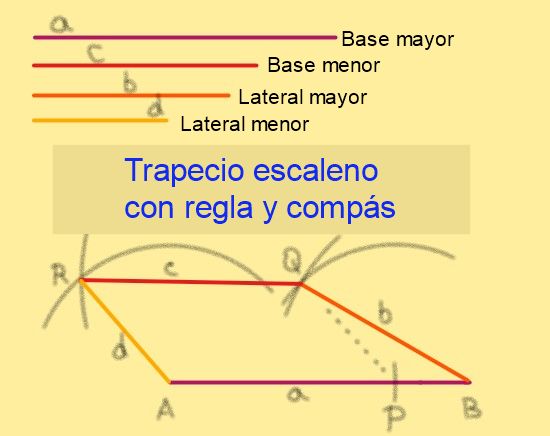
5.- Con centro en A trazar un arco de radio d.
6.- Con centro en Q trazar un arco de radio c que intercepte al arco trazado en el paso anterior. Se llamará R al punto de corte.
7.- Se trazan con la regla los segmentos BQ, QR y RA.
8.- El cuadrilátero ABQR es un trapecio escaleno, ya que APQR es un paralelogramo lo que garantiza que AB || QR.
Se dan las siguientes longitudes en cm: 7, 3, 4 y 6.
a) Determine si con ellas se puede construir un trapecio escaleno que pueda circunscribir a una circunferencia.
b) Halle el perímetro, el área, la longitud de las diagonales y la altura de dicho trapecio, así como el radio de la circunferencia inscrita.
Usando los segmentos de longitud 7 y 3 como bases y los de longitud 4 y 6 como laterales, puede construirse un trapecio escaleno usando el procedimiento descrito en la sección previa.
Falta comprobar si el mismo tiene circunferencia inscrita, pero recordando la propiedad (9):
Un trapecio tiene circunferencia inscrita solo si la suma de sus bases es igual a la suma de sus laterales.
Vemos que efectivamente:
7 + 3 = 4 + 6 =10
Entonces se cumple la condición de existencia de circunferencia inscrita.
Perímetro
El perímetro P se obtiene sumando los lados. Como las bases suman 10 y las laterales también, el perímetro es:
P = 20 cm
Área
Para determinar el área, conocidos solo sus lados se aplica la relación:
A = [(a+c)/|a–c|]∙√[(s-a)(s-c)(s-a-d)(s-a-b)]
Donde s es el semiperímetro:
s = (a+b+c+d)/2.
En nuestro caso, el semiperímetro vale s=10 cm. Después de sustituir los respectivos valores:
a=7 cm; b=6 cm; c=3 cm; d= 4 cm
Queda:
A = [10/4]√[(3)(7)(-1)(-3)] = (5/2)√63 = 19,84 cm².
Altura
La altura h está relacionada con el área A mediante la siguiente expresión:
A=(a+c)∙h/2, de donde puede obtenerse la altura mediante despeje:
h = 2A/(a+c) = 2 * 19,84 / 10 = 3,968 cm.
Radio de la circunferencia inscrita
El radio de la circunferencia inscrita vale la mitad de la altura:
r = h/2 = 1,984 cm
Diagonales
Finalmente se encuentra la longitud de las diagonales:
d1 = √[b2 + a∙c – a(b2 – d2)/(a – c)]
d2 = √[d2 + a∙c – a(d2 – b2)/(a – c)]
Sustituyendo adecuadamente los valores se tiene:
d1 = √[62 + 7∙3 – 7(62 – 42)/(7 – 3)] = √( 36+21-7(20)/4 ) = √(22)
d2 = √[42 + 7∙3 – 7(42 – 62)/(7 – 3)] = √(16+21-7(-20)/4) = √(72)
Es decir: d1 = 4,69 cm y d2 = 8,49 cm
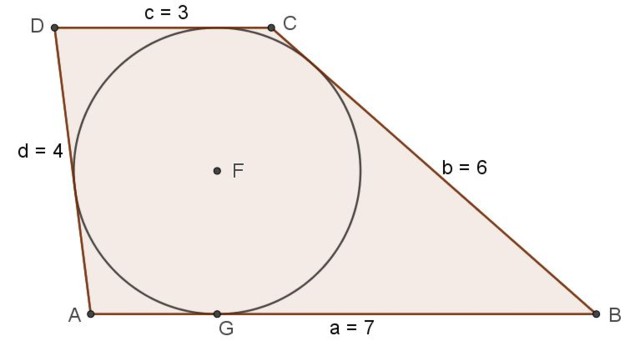
Determinar los ángulos interiores del trapecio de bases AB=a=7, CD=c=3 y laterales BC=b=6 , DA=d= 4.
Puede aplicarse el teorema del coseno para determinar los ángulos. Por ejemplo, el ángulo ∠A=α se determina a partir del triángulo ABD con AB=a=7, BD=d2=8,49 y DA=d=4.
El teorema del coseno aplicado a este triángulo queda así:
d22 = a2 + d2 – 2∙a∙d∙Cos(α), es decir:
72=49+16-56∙Cos(α).
Al despejar, se obtiene el coseno del ángulo α:
Cos(α) = -1/8
Es decir que α = ArcCos(-1/8) = 97,18⁰.
De igual modo se obtienen los otros ángulos, siendo sus valores:
β=41,41⁰; γ=138,59⁰ y finalmente δ=82,82⁰.
- C. E. A. (2003). Elementos de geometría: con ejercicios y geometría del compás. Universidad De Medellín.
- Campos, F., Cerecedo, F. J. (2014). Matemáticas 2. Grupo Editorial Patria.
- Freed, K. (2007). Discover Polygons. Benchmark Education Company.
- Hendrik, V. (2013). Generalized Polygons. Birkhäuser.
- IGER. (s.f.). Matemática Primer Semestre Tacaná. IGER.
- Jr. geometry. (2014). Polygons. Lulu Press, Inc.
- Miller, Heeren, & Hornsby. (2006). Matemática: Razonamiento Y Aplicaciones (Décima Edición). Pearson Educación.
- Patiño, M. (2006). Matemáticas 5. Editorial Progreso.
- Wikipedia. Trapecio. Recuperado de: es.wikipedia.com
