Regla de correspondencia de una función: qué es, ejemplos, ejercicios

¿Qué es la regla de correspondencia de una función?

La regla de correspondencia de una función señala la manera en que los elementos de un conjunto se relacionan con los elementos de otro. A los elementos del primer conjunto se les conoce como el dominio, y a los del segundo, como el codominio o contradominio.

La relación o vínculo entre conjuntos se puede especificar mediante una instrucción verbal o escrita, sin embargo, cuando los conjuntos son numéricos, la regla de correspondencia se indica mediante una fórmula.

Dicha fórmula contiene las operaciones que deben hacerse con los elementos del conjunto de partida, y obtener así una serie de elementos incluidos en el codominio.

Ahora bien, cuando la relación entre los elementos es una función, la regla de correspondencia cumple dos condiciones especiales:

• A cada uno de los elementos del dominio se asocia, mediante la regla de correspondencia, un solo elemento del codominio, conocido como la imagen.
• Dicha imagen es única, en otras palabras, ningún elemento del dominio se asocia a más de un elemento del codominio.

De esta manera, se puede imaginar la regla de correspondencia de una función como un mecanismo encerrado en una caja. Cada valor del dominio, sin excepción, puede entrar a la caja y salir de ella transformado, mediante las operaciones que indique la regla de correspondencia. Enseguida se verán los ejemplos.

Ejemplos

Ejemplo 1

La regla de correspondencia de una función se puede expresar como una instrucción escrita, cuando los elementos no son numéricos.

Por ejemplo, se tiene un conjunto de países, denotado como P, y otro conjunto de ciudades C:

P = {Canadá, México, España, USA, Francia, Argentina, Brasil, Alemania}

C = {París, Londres, Buenos Aires, Berlín, Ciudad de México, Ottawa, Río, Nueva York, Madrid, Washington, Berna, Roma, Brasilia, Toronto}

Sea la regla de correspondencia f entre P y C dada por:

f: P → C

Donde f es la regla “…cuya capital es…”, que asocia a cada país en P (el conjunto de partida), con su ciudad capital en C (el conjunto de llegada).

Por ejemplo: “España, cuya capital es Madrid”. El elemento “España” pertenece al conjunto P de partida, y el elemento “Madrid” al conjunto C, el de llegada.

La representación de esta función se puede hacer a través de un diagrama de Venn o simplemente a través de pares ordenados.

Los pares ordenados contienen, como su nombre lo indica, dos elementos con un orden específico, en este ejemplo, el primer elemento del par es el país, y el segundo, su ciudad capital.

Por su parte, el diagrama de Venn es una manera visualizar gráficamente la función, mostrando los conjuntos de partida y llegada, así como la regla de correspondencia entre ellos.

Representación de f como pares ordenados

f = {(Canadá, Ottawa); (México, Ciudad de México); (España, Madrid); (USA; Washington); (Francia, París); (Argentina, Buenos Aires); (Brasil, Brasilia); (Alemania, Berlín)}

El primer par asocia a Canadá, cuya capital es Ottawa, el segundo asocia a México, cuya capital es Ciudad de México y así sucesivamente.

Representación de f como un diagrama de Venn

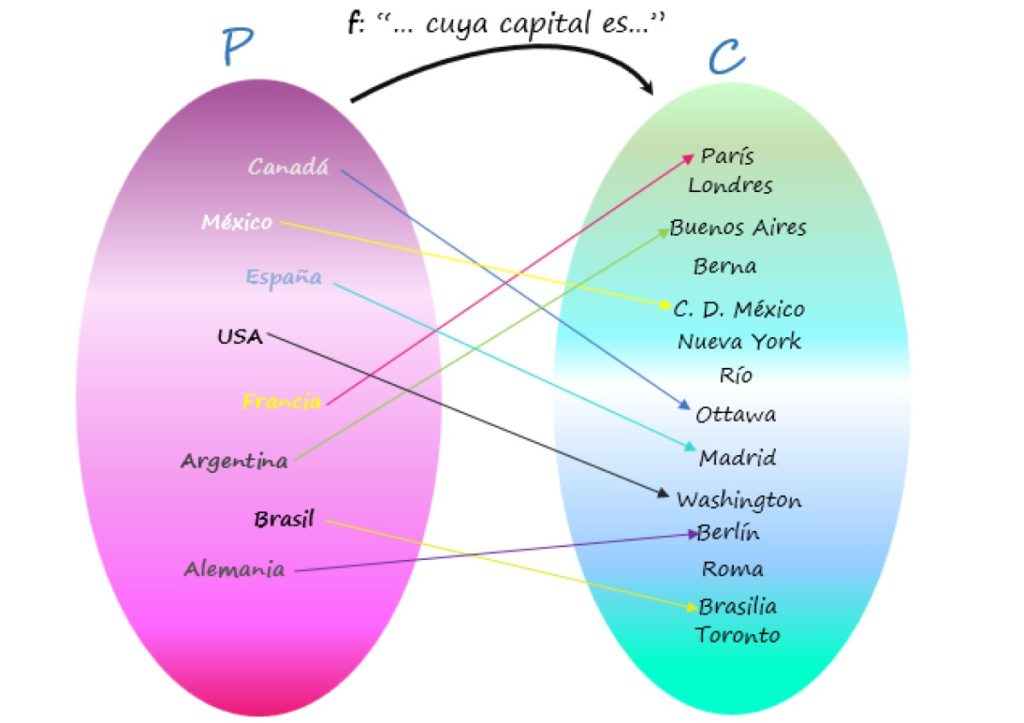
Nótese que hay ciudades que no son capital de algún país, ya que, si bien son elementos del codominio, no son imagen de algún elemento del conjunto de partida. Aún así, la relación es una función, pues lo importante es que cada país tenga su capital, y esta sea única.

El subconjunto formado por los elementos del codominio que son imagen de algún elemento del dominio, se denomina rango o recorrido de la función. Para el ejemplo, el recorrido R de f es:

R = {París, Buenos Aires, Ciudad de México, Ottawa, Madrid, Berlín, Washington, Brasilia}

Cabe preguntarse si se puede establecer una relación entre C y P, donde C pasa a ser el conjunto de partida y P el de llegada. La respuesta es sí, pero no sería una función, pues hay ciudades que no son capitales, como Nueva York, o el país del que son capital no aparece entre los elementos del conjunto P, como Roma.

Ejemplo 2

Cuando el conjunto de partida y el de llegada son numéricos, la regla de correspondencia de la función que los vincula es una fórmula. Por ejemplo, sea el dominio de una función el siguiente conjunto:

D = {0, 1, 2, 3, 4, 5, 6)

La regla de correspondencia f: D → R que vincula a los elementos de D con el conjunto de los números reales R es:

f: “el doble de”

Si “x” es un elemento cualquiera del conjunto de partida, f(x) es el correspondiente elemento del conjunto de llegada, y la regla de correspondencia se escribe así:

f(x) = 2x

El codominio es el conjunto de los números reales. Un subconjunto de los reales es el recorrido de esta función, el conjunto de números cuyo valor es el doble de x:

R = {0, 2, 4, 6, 8, 10, 12}

En forma de pares ordenados, la regla de correspondencia resulta en:

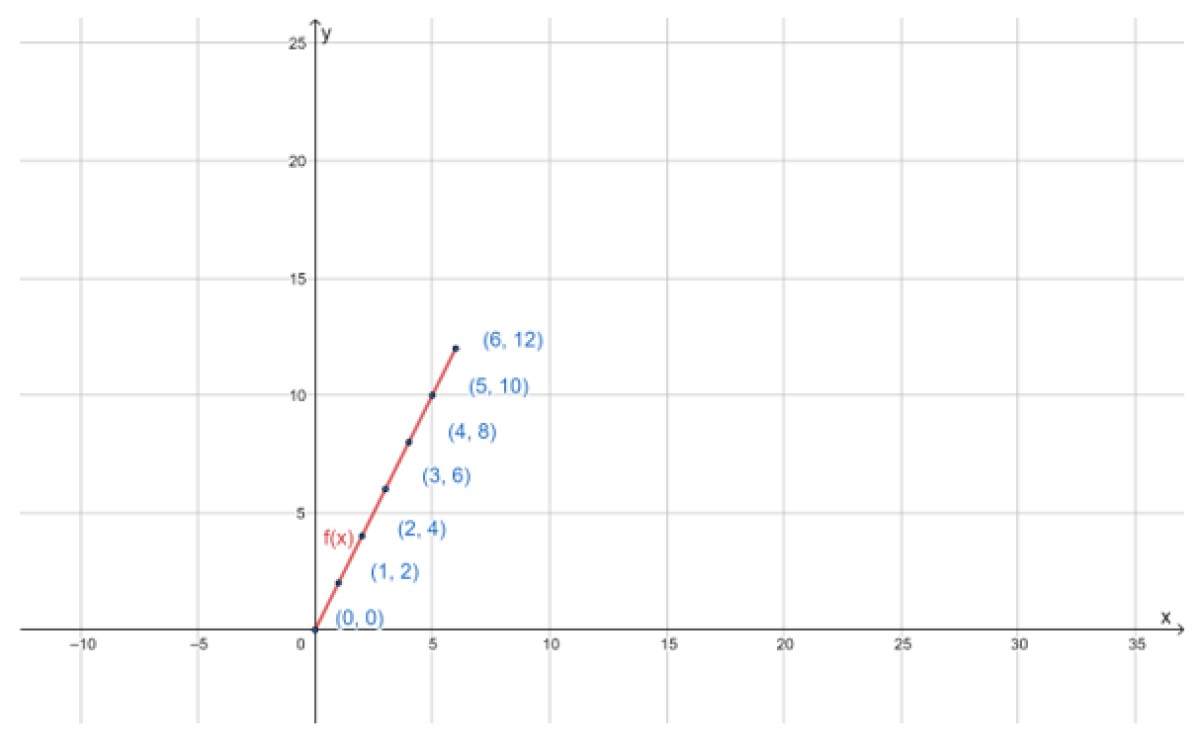
f = {(0,0); (1,2); (2,4); (3,6); (4,8); (5,10); (6,12)}

Los pares ordenados se pueden graficar en el plano cartesiano. El primer elemento del par se coloca en el eje horizontal, llamado también eje de las abscisas o eje “x”, mientras que el segundo va en el eje vertical, eje de las ordenadas o simplemente eje “y”:

Ejercicios

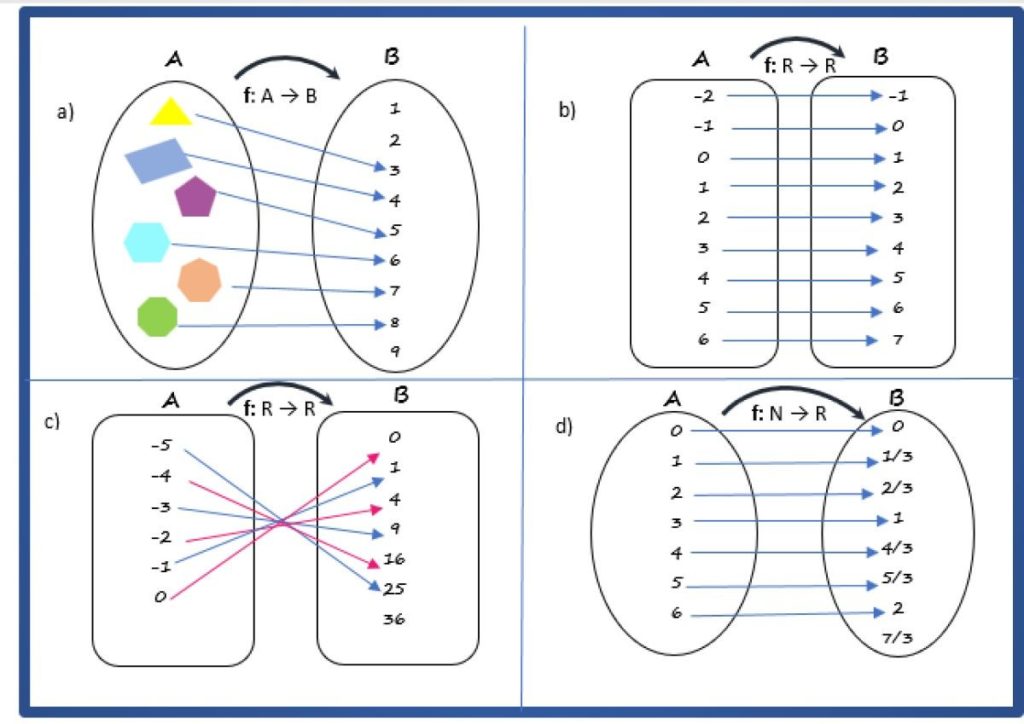
Determinar la regla de correspondencia para las siguientes relaciones, indicando si son o no funciones. El conjunto de los números naturales es N y el de los reales es R.

Señalar además el dominio, el codominio y el recorrido de la función, en los casos en que corresponda:

Solución a

Se trata de una función, ya que cada elemento del conjunto de partida, consistente en polígonos, tiene una imagen única en el conjunto de llegada.

La regla de correspondencia relaciona el polígono con el número de sus lados, el dominio consiste en el conjunto A de los polígonos:

A = {triángulo, cuadrilátero, pentágono, hexágono, heptágono, octágono}

El codominio es el conjunto de los primeros números naturales, incluyendo al 0.

B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Y el recorrido C son los números naturales del 3 al 8:

C = {3, 4, 5, 6, 7, 8}

Solución b

Es una función, ya que cumple las condiciones especificadas anteriormente.

La regla de correspondencia es:

f (x) = x + 1

La regla de correspondencia indica que la función se define de R → R, por lo tanto, el dominio es el conjunto de los números reales. Y el codominio y el recorrido también coinciden con los reales.

Solución c

Es una función, con la regla de correspondencia:

f(x) = x²

El dominio y el codominio son el conjunto de los reales, pero el recorrido consiste únicamente en números reales positivos, denotados como R⁺ e incluyendo el 0.

Solución d

Es una función. Su regla de correspondencia es:

f(x) = x/3

Su dominio es el conjunto de los números naturales N y el codominio, así como el recorrido, son los números reales R.