¿Qué es la frecuencia relativa y cómo se calcula?
La frecuencia estadística se refiere a repetición de un evento o suceso, mientras que la frecuencia relativa se refiere a comparación; es decir, hablar de frecuencia relativa es establecer cuánto se repite un evento en relación con el total de eventos posibles.
Por ejemplo, número de niños de una determinada edad en relación al total de niños de una escuela, o cuántos vehículos deportivos hay entre todos los vehículos que hay en un parking de estacionamiento.
En el contexto del manejo de datos, a veces conviene clasificarlos de acuerdo a alguna característica, por ejemplo los datos censales de población se pueden agrupar por grupos de edades, nivel de ingresos, nivel educativo, etc.
A estas agrupaciones se les denomina clases y a la cantidad de elementos que corresponden a cada clase se le llama frecuencia de clase o absoluta. Cuando se divide la frecuencia entre el número total de datos se obtiene la alícuota.
La alícuota representa esa clase en relación con el total y se conoce como frecuencia relativa, la cual se expresa como una cantidad entre cero y uno o se multiplica por cien y se expresa como porcentaje del total.
Por ejemplo si se tienen 20 niños de 7 años en el patio de una escuela donde hay 100 niños; la frecuencia relativa seria 20/100 = 0.2 o 20%.
Tablas de frecuencia
La frecuencia relativa es uno de los elementos que constituyen una tabla de distribución de frecuencias. Estas tablas presentan la información contenida en un grupo de datos, ordenada por clases, en relación con una característica en particular.
Para su construcción se deben definir: el número de clases, los límites de estas (que deben ser claros y excluyentes), el valor representativo de la clase y las frecuencias.
Amplitud de variación: La diferencia entre el mayor y el menor de los números.
Número de clases: cantidad de clases entre los que distribuiremos los números. Usualmente está entre 5 y 20.
Intervalo de clase: intervalo de valores que definen una clase. Sus extremos se llaman límites inferior y superior.
Marca de clase (xi): punto medio del intervalo de clase o valor representativo de la clase. En teoría se supone que todos los valores en una clase coinciden con este número.
Cálculo de frecuencia relativa
Vamos a construir una tabla de distribución de frecuencias, a manera de ejemplo, y con ella ilustramos cómo se calcula la frecuencia relativa.
Tomaremos del Canavos, 1998, el siguiente caso estudio:
Se quiere saber el salario semanal de los empleados de la empresa P&R, expresados en U.S. $. Para ello, se elige una muestra representativa de 65 empleados.
Se obtienen los siguientes resultados: 251 252,5 314,1 263 305 319,5 265 267,8 304 306,35 262 250 308 302,75 256 258 267 277,55 281,35 255,5 253 259 263 266,75 278 295 296 299,5 263,5 261 260,25 277 272,5 271 286 295 278 279 272,25 286,3 279 296,25 271 272 279 275 277 279 276,75 281 287 286,5 294,25 285 288 296 283,25 281,5 293 284 282 292 299 286 283
1.- Vamos a ordenarlos en orden ascendente
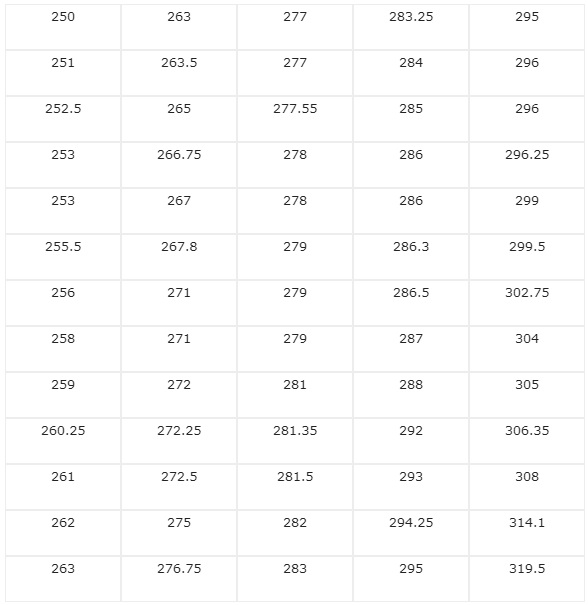
2.- Para construir la tabla de frecuencias debemos definir: Amplitud de Variación, Número de clases e Intervalo de clase
El número de clases se selecciona pensando en que sean pocas clases y en los divisores de la amplitud de variación que es casi 70.
7 clases es un número cómodo de clases a manejar y los intervalos de clase quedarían en 10, el cual es un número ideal para trabajar con datos agrupados.
3.- Construimos una tabla de seis columnas
– Intervalo de clase (Ic), que representa la clase (intervalo de clase), en este caso los límites inferior y superior de los salarios incluidos en la clase.
– Centro de clase (xi), que representa el valor del salario promedio de la clase.
– Frecuencia absoluta (fi), que representa la frecuencia absoluta, en este caso la cantidad de salarios pertenecientes a la clase.
– Frecuencia relativa (hi), es el cociente entre la frecuencia absoluta (fi) y el número total de datos (n), expresada en porcentaje.
– Frecuencia absoluta acumulada (Fi), indica cuántos elementos de la lista de datos son menores o iguales al límite superior de una determinada clase. Es la suma de las frecuencias absolutas desde la primera clase hasta la clase elegida.
– Frecuencia relativa acumulada (Hi), es el cociente entre la frecuencia absoluta acumulada (Fi) y el número total de datos (n), expresada en porcentaje.
La tabla queda:
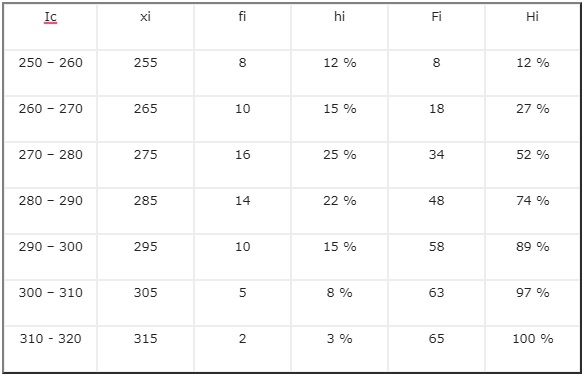
Es de hacer notar que la frecuencia relativa puede ser absoluta o acumulada, y es que el concepto de frecuencia relativa nos ubica en un contexto de comparación con un total. Cualquier cantidad puede ser objeto de cálculo de este tipo de índices.
Por ejemplo, cuando hablamos de porcentaje de estudiantes aprobados en una determinada prueba o examen, este porcentaje es la proporción del total de estudiantes que aprobó la prueba o examen; es decir, es una cantidad relativa al total de estudiantes.
Bibliografía consultada
- Canavos, G. 1988. Probabilidad y Estadística. Aplicaciones y métodos. McGraw-Hill/Interamericana de México S. A. de C. V. México. 667 p.
- Freund, R. and Wilson, W. 2003. Statistical methods. Second ed. Academic Press. An imprint of Elsevier Science. San Diego. USA. 694 p.
- Sokal, R. and Rohlf, F. 1979. Biometría. Principios y métodos estadísticos en la investigación biológica. H. Blume Ediciones. México. 832 p.
- Spiegel, M. 1991. Estadística. Segunda ed. McGraw-Hill/Interamericana de España S. A. Madrid. 572 p.
- Walpole, R., Myers, R., Myers, S. and Ye, Ka. 2007. Probability & Statistics for engineers & scientists. Eighth ed. Pearson Education Internacional Prentice Hall. New Jersey. USA. 823 p.
