Velocidad media: fórmulas, cómo se calcula y ejercicio resuelto

La velocidad media para una partícula móvil se define como la razón entre la variación de la posición que ella experimenta y el intervalo de tiempo empleado en el cambio. La situación más sencilla es aquella en la cual la partícula se mueve a lo largo de una línea recta representada por el eje x.

Supóngase que el objeto móvil ocupa las posiciones x₁ y x₂ en los tiempos t₁ y t₂ respectivamente. La definición de velocidad media v_m se representa matemáticamente así:

Las unidades de v_m en Sistema Internacional son metros/segundo (m/s). Otras unidades de uso común que aparecen en textos y dispositivos móviles son: km/h, cm/s, millas/h, pies/s y más, siempre que sean de la forma longitud/tiempo.

La letra griega “Δ” se lee “delta” y se utiliza para indicar resumidamente la diferencia entre dos cantidades.

Índice del artículo

• 1 Características del vector velocidad media vm
• 2 Los signos de la velocidad media
• 3 La rapidez media: una magnitud escalar
• 4 Ejercicio resuelto
• 5 Referencias

Características del vector velocidad media v_m

La velocidad media es un vector, ya que está relacionado con el cambio de posición, el cual a su vez se conoce como vector desplazamiento.

Esta cualidad se representa en negritas o mediante una flecha encima de la letra que designa la magnitud. Sin embargo en una dimensión, la única dirección posible es la del eje x y por lo tanto se puede prescindir de la notación vectorial.

Puesto que los vectores tienen magnitud, dirección y sentido, un vistazo inicial a la ecuación indica que la velocidad media tendrá la misma dirección y sentido que el desplazamiento.

Imaginemos a la partícula del ejemplo moviéndose a lo largo de una línea recta. Para describir su movimiento, es necesario indicar un punto de referencia, el cual será el “origen” y se denotará como O.

La partícula puede moverse alejándose o acercándose a O, bien sea hacia la izquierda o hacia la derecha. También puede emplear mucho o poco tiempo en llegar a una posición determinada.

Las magnitudes que se han mencionado: posición, desplazamiento, intervalo de tiempo y velocidad media, describen el comportamiento de la partícula mientras se mueve. Se trata de las magnitudes cinemáticas.

Para distinguir las posiciones o ubicaciones a la izquierda de O se emplea el signo (-) y las que se encuentran a la derecha de O llevan el signo (+).

La velocidad media tiene una interpretación geométrica que se aprecia en la siguiente figura. Es la pendiente de la recta que pasa por los puntos P y Q. Al cortar a la curva posición vs. tiempo en dos puntos, se trata de una recta secante.

Los signos de la velocidad media

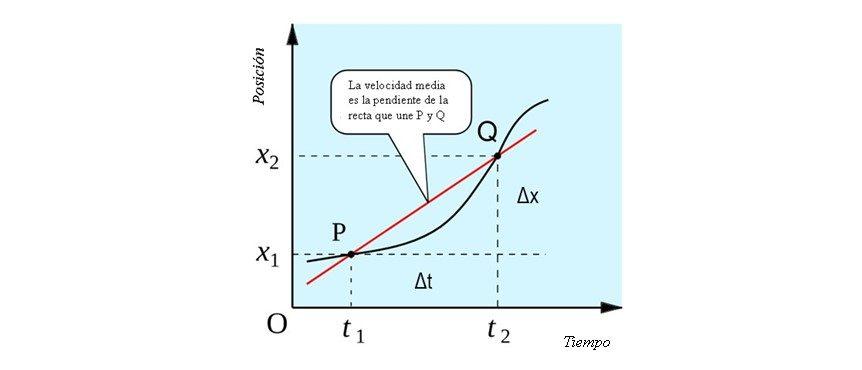
Para el siguiente análisis debe tenerse en cuenta que t₂ > t₁. Es decir, el instante siguiente siempre es mayor al actual. De esta manera t₂ – t₁ siempre es positivo, lo cual suele tener sentido cotidianamente.

Entonces el signo de la velocidad media estará determinado por el de x₂ – x₁. Nótese que es importante tener claro dónde está el punto O  -el origen-, ya que este es el punto respecto al cual se dice que la partícula va “hacia la derecha” o “hacia la izquierda”.

O bien “hacia adelante” o “hacia atrás”, como el lector prefiera.

Si la velocidad media es positiva significa que en promedio el valor de “x” aumenta con el tiempo, aunque ello no quita que pudo haber disminuido en algún momento del lapso tiempo considerado – Δt -.

Sin embargo en términos globales, al finalizar el tiempo Δt, ella terminó con una posición más grande que la que tenía al comienzo. Los detalles del movimiento son ignorados en este análisis.

¿Y si la velocidad media resulta negativa? Pues quiere decir entonces que la partícula finaliza con una coordenada más pequeña que aquella con la cual inició. A groso modo se movió hacia atrás. Veamos algunos ejemplos numéricos:

Ejemplo 1: Dadas las posiciones inicial y final señaladas, indique el signo de la velocidad media. ¿Hacia donde se movió globalmente la partícula?

a) x₁ = 3 m ; x₂ = 8 m

Respuesta: x₂– x₁  = 8 m – 3 m = 5 m. Velocidad media positiva, la partícula se movió hacia adelante.

b) x₁ = 2 m ; x₂ = -3 m

Respuesta: x₂ – x₁ = -3 m – 2 m = -5 m. Velocidad media negativa, la partícula se movió hacia atrás.

 c) x₁  = – 5 m ; x₂ = -12 m

Respuesta: x₂ – x₁   = -12 m – (-5 m) = -7 m. Velocidad media negativa, la partícula se movió hacia atrás.

d) x₁  = – 4 m ; x₂ = 10 m

Respuesta: x₂ – x₁  = 10 m – (-4m) = 14 m. Velocidad media positiva, la partícula se movió hacia adelante.

¿Puede la velocidad media ser 0? Sí. Con tal de que el punto de partida y el de llegada sean el mismo. ¿Significa esto que la partícula estuvo necesariamente en reposo todo el tiempo?

No, solamente significa que el viaje fue de ida y vuelta. Tal vez viajó rápidamente o quizá muy lentamente. Por ahora no se sabe.

La rapidez media: una magnitud escalar

Ello nos lleva a definir un nuevo término: la rapidez media. En Física es importante distinguir entre las magnitudes vectoriales y las magnitudes que no lo son: las escalares.

Para la partícula que hizo el viaje de ida y vuelta, la velocidad media es 0, pero pudo haber sido muy veloz o tal vez no. Para saberlo se define  la rapidez media como:

Las unidades de la rapidez media son las mismas que las de la velocidad media. La diferencia fundamental entre ambas magnitudes es que la velocidad media incluye interesante información acerca de la dirección y el sentido de la partícula.

En cambio la rapidez media brinda únicamente información numérica. Con ella se sabe que tan rápido o lento se movió la partícula, pero no si lo hizo hacia adelante o hacia atrás. Por eso es una magnitud escalar. ¿Cómo distinguirlas al denotarlas? Una forma es dejando las negritas para los vectores, o colocando sobre estos una flechita.

Y es importante notar que la velocidad media no tiene que ser igual a la rapidez media. Para el viaje de ida y vuelta la velocidad media es nula, pero la rapidez media no. Ambas tienen el mismo valor numérico cuando se viaja siempre en una misma dirección.

Ejercicio resuelto

Usted conduce de vuelta a casa desde la escuela tranquilamente a 95 km/h por 130 km. Comienza a llover y reduce la velocidad a 65 km/h. Por fin llega a casa después de conducir durante 3 horas y 20 minutos.

a) ¿Qué tan lejos está su casa de la escuela?

b) ¿Cuál fue la rapidez media?

Respuestas:

a) Son necesarios algunos cálculos previos:

El viaje se divide en dos partes, la distancia total es:

d = d1 + d₂, con d1 = 130 km

t2 = 3.33 – 1.37 horas = 1.96 horas

Cálculo de d_2:

d₂ = 65 km/h x 1.96 h = 125. 4 km.

La escuela dista d1 + d₂ = 255.4 km de la casa.

b) Ahora se puede encontrar la rapidez media:

Referencias

1. Giancoli, D. Physics. Principles with Applications. Sixth Edition. Prentice Hall. 21- 22.
2. Resnick, R. (1999). Física. Volumen 1. Tercera edición en español. México. Compañía Editorial Continental S.A. de C.V. 20-21.
3. Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Edición. México. Cengage Learning Editores. 21-23.