Fracciones equivalentes a 2/3: explicación, ejemplos y ejercicios
Las fracciones equivalentes a ⅔ (se lee dos tercios) son aquellas cuyo valor, expresado en forma decimal, es el mismo que se obtiene al dividir 2 entre 3: 0.6666… Los puntos suspensivos indican que el 6 aparece infinitas veces en esta división.
Una fracción equivalente a 2/3 es la fracción 4/6, pues resulta que tras resolver la división entre 4 y 6 de manera explícita, se obtiene el decimal 0,66666…. Entonces puede afirmarse que 4/6 = 2/3 = 0,66666….

Una fracción, como su nombre lo indica, es una parte o porción de la unidad. La fracción ⅔ se obtiene al dividir la unidad en tres partes iguales y tomar dos de esas partes.
Toda fracción consta de una parte superior, llamada numerador, separada de la parte inferior o denominador, mediante la línea de fracción. El denominador indica en cuántas partes se divide la unidad y el numerador señala cuántas de estas partes hay que tomar en consideración.
Ahora considérese la a fracción 4/6 (se lee cuatro sextos). Se comprueba que esta fracción es equivalente a ⅔, ya que para dividir la unidad en seis partes, hay que seguir estos pasos:
- Dividir la unidad en tres partes iguales.
- Y después dividir cada una de estas partes a la mitad, obteniéndose en total seis partes iguales.
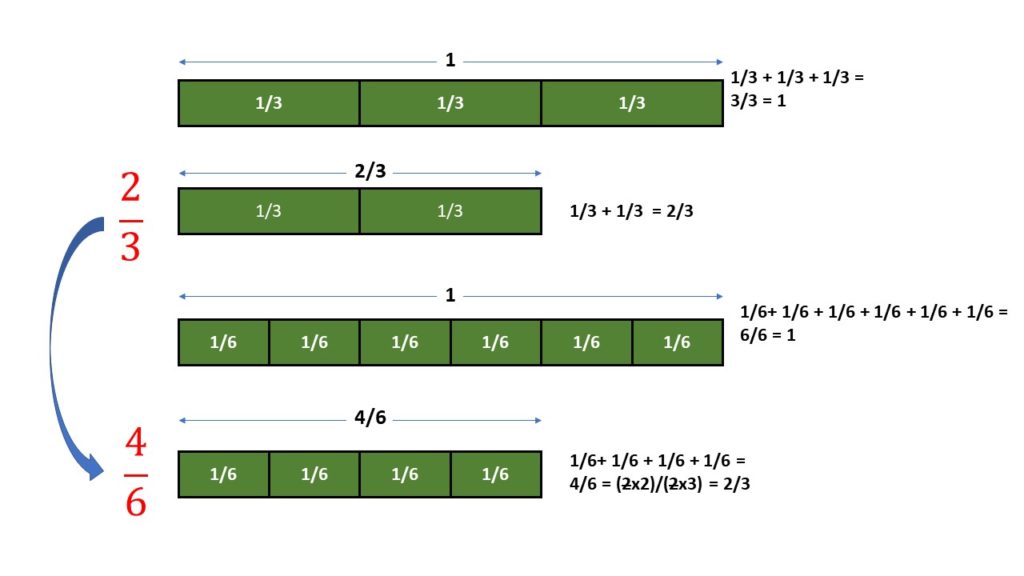
Verificación gráfica de que la fracción 2/3 es equivalente a la fracción 4/6. Fuente: F. Zapata.
Métodos para encontrar fracciones equivalentes
Obsérvese que la fracción equivalente 4/6 se puede obtener de 2/3 al multiplicar por 2 tanto al numerador como al denominador de esta última.
Cuando se multiplica simultáneamente el numerador y el denominador de una fracción por un mismo número, se obtiene una fracción equivalente.
Otra manera de encontrar una fracción equivalente a otra sería dividiendo numerador y denominador por una misma cantidad, siempre que el numerador y el denominador sea divisible en forma exacta por ese mismo número. Pero no es posible conseguir, mediante la división por un mismo entero, una fracción equivalente partiendo de 2/3, ya que los números 2 y 3 son primos entre sí.
Cuando el numerador y el denominador de una fracción son números primos entre sí, se dice que la fracción es irreducible. Y la fracción 2/3 es un buen ejemplo de esta clase de fracciones, de hecho, 2/3 representa al conjunto de todas las fracciones equivalentes a 0.666…
En cambio la fracción 4/6 es reducible y equivalente a la fracción ⅔, ya que el numerador 4 y el denominador 6 son números pares, ambos divisibles por 2.
Entonces, las dos formas de obtener fracciones equivalentes a una dada, son:
- Amplificar simultáneamente numerador y denominador
- Reducir conjuntamente numerador y denominador
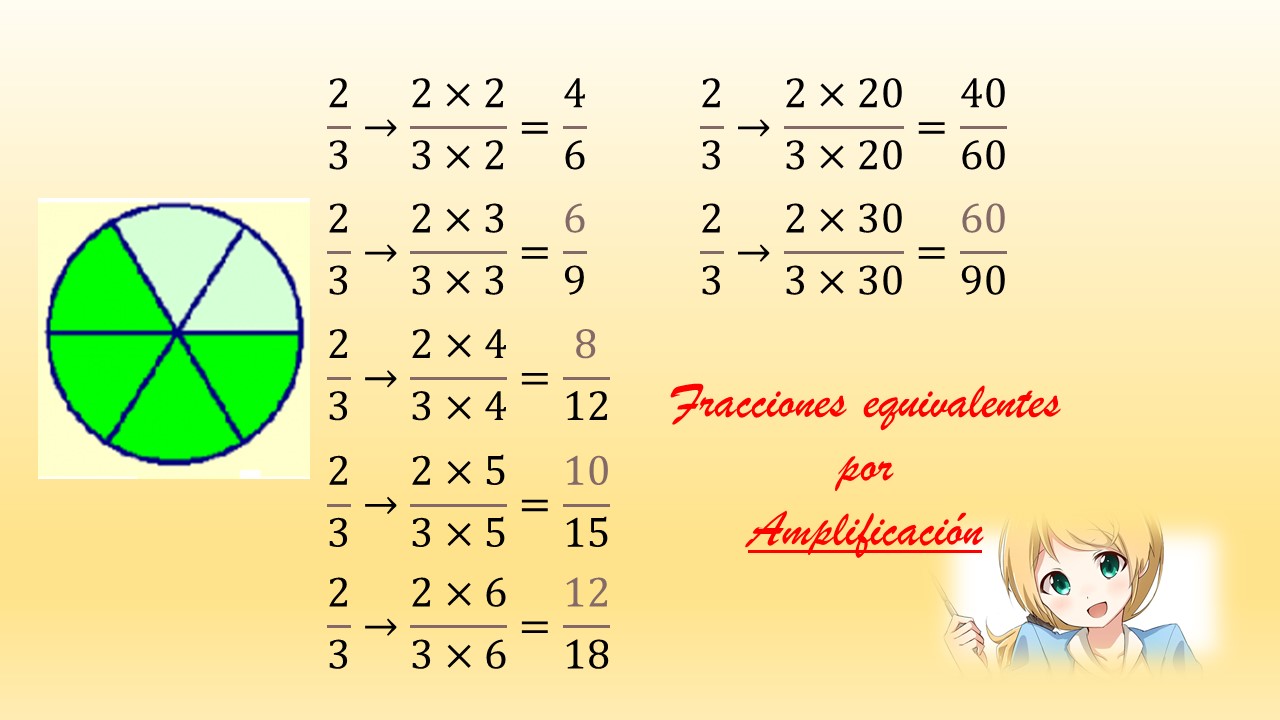
Amplificación de fracciones
Para obtener una fracción equivalente a una dada, se multiplican numerador y denominador por una misma cifra. Aquí hay algunos ejemplos:
En resumen, si se parte de la fracción irreducible ⅔, la forma de obtener cualquier otra fracción equivalente, es aplicar esta fórmula:
Reducción de fracciones
Es un método que permite obtener una fracción equivalente, siempre que la fracción de partida tenga numerador y denominador con uno o más divisores comunes.
No es el caso de 2/3, que como se dijo antes, es irreducible. Pero por ejemplo, la fracción 60/90 (sesenta noventavos) puede reducirse a:
- 6/9, ya que tanto el numerador como el denominador son divisibles entre diez.
- 30/45, porque numerador y denominador son divisibles entre dos.
- 20/30, ya que numerador y denominador son divisibles entre tres.
- 12/18, debido a que numerador y denominador son divisibles entre cinco.
Si se quiere obtener la fracción irreducible equivalente a la original, entonces es necesario dividir tanto numerador como denominador por su Máximo Común Divisor (MCD).
Descomponiendo en factores el numerador se tiene:
60 = 22 ⋅ 3 ⋅ 5
Y llevando a cabo el mismo procedimiento en el denominador:
90 = 2 ⋅ 32 ⋅ 5
El MCM son los factores primos comunes con su menor exponente, es decir:
MCM(60; 90)= 2⋅3⋅5 = 30
Entonces, 60 entre 30 da 2, el cual se coloca en el numerador y como 90 entre 30 da 3, se coloca 3 en el denominador. Por tanto se puede expresar la fracción irreducible de 60/90 como:
Formas de determinar si una fracción dada es equivalente a 2/3
La manera directa para saber si dos o más fracciones son equivalentes, es expresar las fracciones directamente en forma decimal, y si todos los dígitos coinciden, es seguro que las fracciones son equivalentes. Pero hay otros métodos aplicables a 2/3:
Método 1
Sea la fracción x/y y se quiere saber si dicha fracción es equivalente a 2/3:
Se coloca un signo de interrogación, pues no se sabe aún si los valores de “x” y “y” satisfacen la igualdad. Para saberlo se multiplica en cruz:
3x =? 2y
Solo cuando la igualdad se cumple, hay seguridad de que x/y es una fracción equivalente a 2/3.
Método 2
Este método requiere determinar máximo común divisor (MCD) del numerador y el denominador. Después ambos se dividen por el MCD, y si la fracción obtenida después de efectuar la operación descrita es 2/3, entonces puede afirmarse que se trata de una fracción equivalente a ella.
Ejemplos
Ejemplo 1
Determinar si la fracción 40/60 es equivalente a ⅔.
Solución
Por el método 1:
El método señala que se debe multiplicar en cruz:
40 x 3 =? 60 x 2
120 =? 120
Puesto que la igualdad se cumple, se concluye que 40/60 es equivalente a 2/3.
Ejemplo 2
Determine si la fracción 120/180 es equivalente a ⅔.
Solución
En este ejemplo se aplica el método 2. Lo primero es determinar la descomposición en factores primos de 120:
120 = 23 ⋅ 3 ⋅ 5
Y la descomposición en factores del denominador es:
180 = 22 ⋅ 32 ⋅ 5
Para determinar el MCD, se multiplican los factores comunes con su menor exponente:
MCD(120; 180)= 22 ⋅ 3 ⋅ 5 = 60
Entonces:
120 ÷ 60 = 2
180 ÷ 60 = 3
Por lo que se concluye que 120/180 es equivalente a 2/3, es decir:
Ejercicios resueltos
Ejercicio 1
¿Son equivalentes las fracciones 10/15 y 12/18?
Solución
La forma más rápida de comprobarlo es multiplicar en cruz, ya que no son valores muy grandes:
10 x 18 =? 15 x 12
180 =? 180
Se obtuvo una igualdad, entonces puede afirmarse que 10/15 = 12/18.
Ejercicio 2
¿Son las fracciones 8/12 y 12/20 equivalentes a ⅔?
Solución
Se aplicará el método de simplificación, que consiste en ir dividiendo simultáneamente numerador y denominador por factores primos comunes hasta llegar a una expresión irreducible:
8/12 = 4/6 = ⅔, es decir que la primera fracción es equivalente a ⅔.
Para la segunda fracción se tiene:
12/20 = 6/10 = ⅗, pero ⅗ es irreducible y diferente de ⅔, por tanto la segunda fracción no equivale a ⅔.
