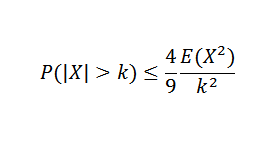Teorema de Chebyshov: que es, aplicaciones y ejemplos
El teorema de Chebyshov (o desigualdad de Chebyshov) es uno de los resultados clásicos más importantes de la teoría de la probabilidad. Permite estimar la probabilidad de un evento descrito en términos de una variable aleatoria X, al proveernos de una cota que no depende de la distribución de la variable aleatoria sino de la varianza de X.
El teorema recibe el nombre en honor al matemático ruso Pafnuty Chebyshov (también escrito como Chebychev o Tchebycheff) quien, a pesar de no ser el primero en enunciar dicho teorema, fue el primero en dar una demostración en el año 1867.
Esta desigualdad, o aquellas que por sus características son llamadas desigualdad de Chebyshov, se usa principalmente para aproximar probabilidades por medio de cálculo de cotas.
¿En qué consiste el teorema de Chebyshov?
En el estudio de la teoría de la probabilidad ocurre que si se conoce la función de distribución de una variable aleatoria X, se puede calcular su valor esperado —o esperanza matemática E(X)— y su varianza Var(X), siempre y cuando dichas cantidades existan. Sin embargo, el recíproco no es necesariamente cierto.
Es decir, conociendo E(X) y Var(X) no necesariamente se puede obtener la función de distribución de X, por lo cual cantidades como P(|X|>k) para algún k>0, son muy difíciles de obtener. Pero gracias a la desigualdad de Chebyshov es posible hacer una estimación de la probabilidad de la variable aleatoria.
El teorema de Chebyshov nos dice que si tenemos una variable aleatoria X sobre un espacio muestral S con una función de probabilidad p, y si k>0, entonces:
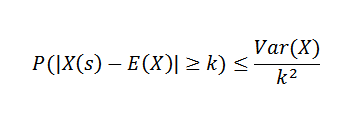
Aplicaciones y ejemplos
Dentro de las muchas aplicaciones que posee el teorema de Chebyshov se pueden mencionar las siguientes:
1. Acotamiento de probabilidades
Esta es la aplicación más común y se utiliza para dar una cota superior para P(|X-E(X)|≥k) donde k>0, solo con la varianza y la esperanza de la variable aleatoria X, sin conocer la función de probabilidad.
Ejemplo 1
Supongamos que el número de productos fabricados en una empresa durante una semana es una variable aleatoria con promedio de 50.
Si se sabe que la varianza de una semana de producción es igual a 25, entonces ¿qué podemos decir acerca de la probabilidad de que en esta semana la producción difiera en más de 10 a la media?
Solución
Aplicando la desigualdad de Chebyshov tenemos que:
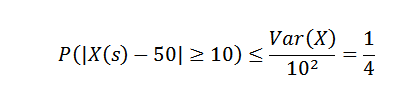
De esto podemos obtener que la probabilidad de que en la semana de producción el número de artículos exceda en más de 10 a la media es a lo más 1/4.
2. Demostración de los teoremas límites
La desigualdad de Chebyshov juega un papel importante en la demostración de los teoremas límites más importantes. Como ejemplo tenemos los siguientes:
Ley débil de los grandes números
Esta ley establece que dada una sucesión X1, X2,…,Xn,… de variables aleatorias independientes con la misma distribución promedio E(Xi)=μ y varianza Var(X)=σ2, y una muestra media conocida de:
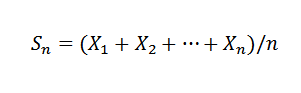
Entonces para k>0 se tiene que:
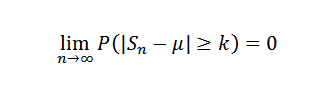
O, de manera equivalente:
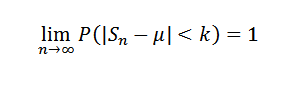
Demostración
Primero notemos lo siguiente:
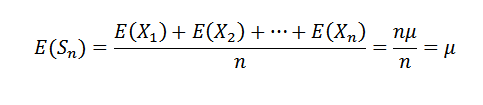
Como X1, X2,…, Xn son independientes, se deduce que:
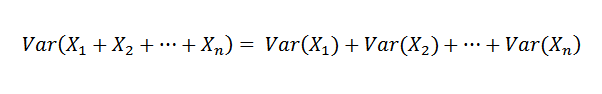
Por lo tanto, es posible afirmar lo siguiente:
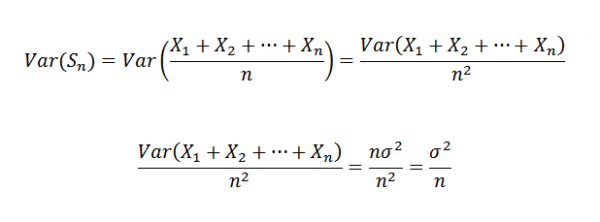
Luego, usando el teorema de Chebyshov se tiene que:
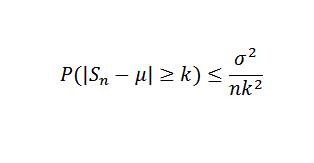
Finalmente, el teorema resulta del hecho de que el límite a la derecha es cero cuando n tiende a infinito.
Cabe resaltar que esta prueba se hizo solo para el caso en el que exista la varianza de Xi; es decir, que no diverge. Así observamos que el teorema siempre es verdadero si E(Xi) existe.
Teorema límite de Chebyshov
Si X1, X2,…, Xn,… es una sucesión de variables aleatorias independientes tal que existe algún C infinito, tal que Var(Xn) ≤ C para todo n natural, entonces para cualquier k>0:
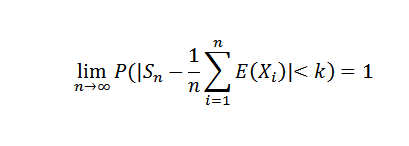
Demostración
Como la sucesión de varianzas es uniformemente acotada, tenemos que Var(Sn)≤ C/n, para todo n natural. Pero sabemos que:
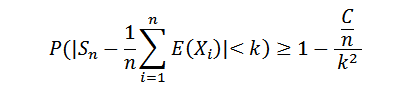
Haciendo tender n hacia infinito, resulta lo siguiente:
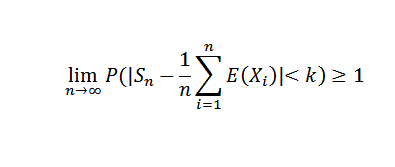
Como una probabilidad no puede exceder el valor de 1, se obtiene el resultado deseado. Como consecuencia de este teorema podríamos mencionar el caso particular de Bernoulli.
Si un experimento se repite n veces de forma independiente con dos resultados posibles (fracaso y éxito), donde p es la probabilidad de éxito en cada experimento y X es la variable aleatoria que representa el número de éxitos obtenidos, entonces para cada k>0 se tiene que:
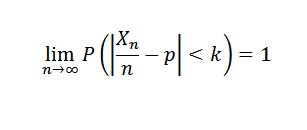
3. Tamaño de muestra
En términos de la varianza, la desigualdad de Chebyshov nos permite encontrar un tamaño de muestra n que es suficiente para garantizar que la probabilidad de que |Sn-μ|>=k ocurra sea tan pequeña como se desee, lo cual permite tener una aproximación a la media.
De manera precisa, sea X1,X2,…Xn una muestra de variables aleatorias independientes de tamaño n y supongamos que E(Xi)=μ y su varianza σ2. Entonces, por la desigualdad de Chebyshov se tiene que:
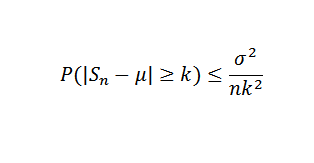
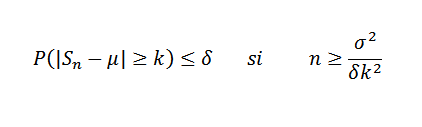
Ejemplo
Supóngase que X1,X2,…Xn son una muestra de variables aleatorias independientes con distribución de Bernoulli, de tal forma que toman el valor 1 con probabilidad p=0.5.
¿Cuál debe ser el tamaño de la muestra para poder garantizar que la probabilidad de que la diferencia entre la media aritmética Sn y su valor esperado (que exceda en más de 0,1), sea menor o igual que 0.,01?
Solución
Tenemos que E(X)=μ=p=0,5 y que Var(X)=σ2=p(1-p)=0,25. Por la desigualdad de Chebyshov, para cualquier k>0 tenemos que:
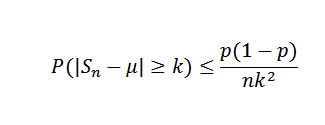
Ahora, tomando k=0,1 y δ=0,01, se tiene que:

De esta manera se concluye que se necesita un tamaño de muestra de al menos 2500 para garantizar que la probabilidad del evento |Sn – 0,5|>= 0,1 sea menor que 0,01.
Desigualdades tipo Chebyshov
Existen diversas desigualdades relacionadas con la desigualdad de Chebyshov. Una de las más conocidas es la desigualdad de Markov:

En esta expresión X es una variable aleatoria no negativa con k,r>0.
La desigualdad de Markov puede tomar distintas formas. Por ejemplo, sea Y una variable aleatoria no negativa (por lo que P(Y>=0)=1) y supongamos que E(Y)=μ existe. Supongamos también que (E(Y))r=μr existe para algún entero r>1. Entonces:
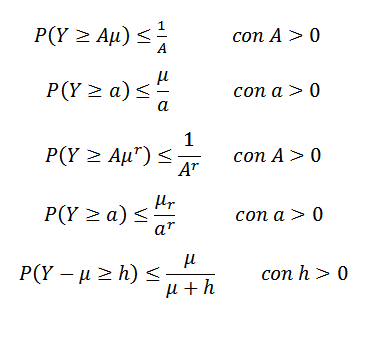
Otra desigualdad es la de Gauss, la cual nos dice que dada una variable aleatoria unimodal X con moda en cero, entonces para k > 0,