Potencial eléctrico: fórmula y ecuaciones, cálculo, ejemplos, ejercicios
El potencial eléctrico se define en cualquier punto donde exista campo eléctrico, como la energía potencial de dicho campo por unidad de carga. Cargas puntuales y distribuciones de cargas puntuales o continuas producen campo eléctrico y por lo tanto tienen asociado un potencial.
En el Sistema Internacional de Unidades (SI), el potencial eléctrico se mide en voltios (V) y se denota como V. Matemáticamente se expresa como:
V = U/qo

Donde U es la energía potencial asociada a la carga o a la distribución y qo es una carga de prueba positiva. Puesto que U es un escalar, el potencial también lo es.
A partir de la definición, 1 voltio es simplemente 1 Joule /Coulomb (J/C), donde Joule es la unidad SI para la energía y Coulomb (C) es la unidad para la carga eléctrica.
Supongamos una carga puntual q. Podemos comprobar la naturaleza del campo que esta carga produce mediante una carga de prueba positiva y pequeña, llamada qo, utilizada a modo de sonda.
El trabajo W necesario para mover esta pequeña carga desde el punto a hasta el punto b, es el negativo de la diferencia de energía potencial ΔU entre dichos puntos:
Wa→ b = -ΔU = – (Ub – Ua)
Dividiendo todo entre qo:
Wa→b /qo= – ΔU / qo = – (Ub – Ua) /qo = – (Vb – Va) = -ΔV
Aquí Vb es el potencial en el punto b y Va es el del punto a. La diferencia de potencial Va – Vb es el potencial de a respecto de b y se denomina Vab. El orden de los subíndices es importante, si se cambiara, entonces representaría el potencial de b respecto de a.
Índice del artículo
- 1 Diferencia de potencial eléctrico
- 2 ¿Cómo calcular el potencial eléctrico?
- 3 Ejemplos de potencial eléctrico
- 4 Ejercicio resuelto
- 5 Referencias
De lo señalado anteriormente se desprende que:
-ΔV = Wa→b /qo
Por lo tanto:
ΔV = -Wa→b /qo
Ahora bien, el trabajo se calcula como la integral del producto escalar entre la fuerza eléctrica F entre q y qo y el vector desplazamiento dℓ entre los puntos a y b. Como el campo eléctrico es fuerza por unidad de carga:
E = F/qo
El trabajo para llevar la carga de prueba desde a hasta b es:
Esta ecuación ofrece la manera para calcular directamente la diferencia de potencial si previamente se conoce el campo eléctrico de la carga o de la distribución que lo produce.
Y también se advierte que la diferencia de potencial es una cantidad escalar, a diferencia del campo eléctrico, que es un vector.
De la definición anterior observamos que si E y dℓ son perpendiculares, la diferencia de potencial ΔV es cero. Esto no significa que el potencial en tales puntos sea cero, sino que simplemente Va = Vb, es decir, el potencial es constante.
Las líneas y las superficies donde esto sucede se denominan equipotenciales. Por ejemplo, las líneas equipotenciales del campo de una carga puntual son circunferencias concéntricas a la carga. Y las superficies equipotenciales son esferas concéntricas.
Si el potencial lo produce una carga positiva, cuyo campo eléctrico consiste en líneas radiales salientes a la carga, al alejarnos del campo el potencial se irá haciendo cada vez menor. Como la carga de prueba qo es positiva, siente menos repulsión electrostática mientras más lejos se encuentre de q.
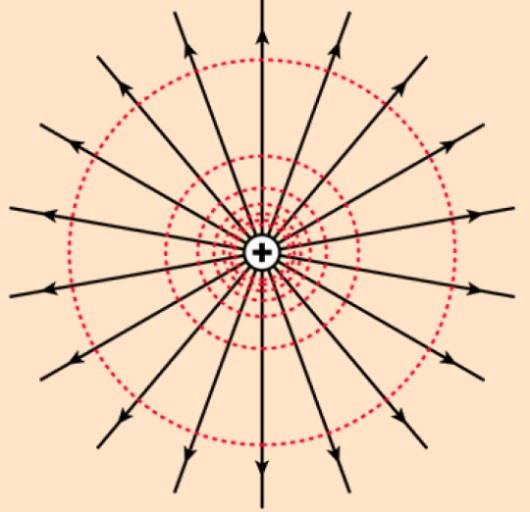
Por el contrario, si la carga q es negativa, la carga de prueba qo (positiva) estará a menor potencial conforme se acerca más a q.
La integral dada anteriormente sirve para encontrar la diferencia de potencial, y por ende el potencial en un punto dado b, si se conoce el potencial de referencia en otro punto a.
Por ejemplo, está el caso de una carga puntual q, cuyo vector campo eléctrico en un punto situado a una distancia r de la carga es:
E =kq/r2r
Donde k es la constante electrostática cuyo valor en unidades del Sistema Internacional es:
k= 9 x 10 9 Nm2 /C2.
Y el vector r es el vector unitario a lo largo de la línea que une a q con el punto P.
Se sustituye en la definición de ΔV:
Eligiendo que el punto b esté a una distancia r de la carga y que cuando a → ∞ el potencial valga 0, entonces Va = 0 y la ecuación anterior queda como:
V = kq/r
Elegir Va = 0 cuando a → ∞ tiene sentido, pues en un punto muy alejado de la carga, es difícil percibir que ella existe.
Cuando hay muchas cargas puntuales distribuidas en una región, se calcula el potencial eléctrico que ellas producen en cualquier punto P del espacio, sumando los potenciales individuales que produce cada una. Así:
V = V1 + V2 + V3 + … VN = ∑ Vi
La sumatoria se extiende desde i = hasta N y el potencial de cada carga se calcula mediante la ecuación dada en la sección anterior.
Partiendo del potencial de una carga puntual, se puede encontrar el potencial que produce un objeto cargado, con un tamaño mensurable, en un punto P cualquiera.
Para ello se divide al cuerpo en muchas pequeñas cargas infinitesimales dq. Cada una contribuye al potencial total con un dV infinitesimal.
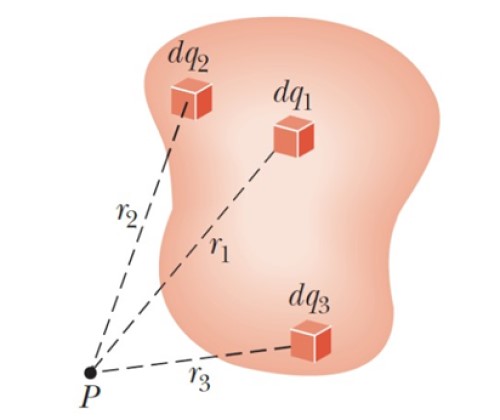
Luego se suman todas estas contribuciones mediante una integral y se obtiene así el potencial total:
Hay potencial eléctrico en diversos dispositivos gracias a los cuales es posible conseguir energía eléctrica, por ejemplo pilas, baterías de automóviles y tomas de corriente. Los potenciales eléctricos también se establecen en la naturaleza cuando hay tormentas eléctricas.
En las pilas y baterías se almacena energía eléctrica a través de las reacciones químicas en su interior. Estas se producen cuando el circuito se cierra, permitiendo que fluya la corriente continua y se encienda un bombillo, o funcione el motor de arranque del automóvil.
Las hay de diversos voltajes: 1.5 V, 3 V, 9 V y 12 V son los más usuales.
A una toma empotrada en la pared se conectan artefactos y electrodomésticos que funcionan con la electricidad comercial de corriente alterna. Dependiendo del lugar, el voltaje puede ser 120 V o 240 V.

Es el que se produce durante las tormentas eléctricas, a causa del movimiento de carga eléctrica a través de la atmósfera. Puede ser del orden de 108 V.

Gracias a una cinta de goma transportadora se produce carga por frotamiento, la cual se acumula sobre una esfera conductora puesta encima de un cilindro aislante. Se genera así una diferencia de potencial que puede ser de varios millones de voltios.

En el corazón hay células especializadas que se polarizan y despolarizan originando diferencias de potencial. Estas pueden ser medidas en función del tiempo mediante un electrocardiograma.
Este examen sencillo se lleva a cabo colocando electrodos sobre el pecho de la persona, capaces de medir las pequeñas señales.
Como son voltajes muy bajos, hay que amplificarlos convenientemente, para luego grabarlos en una cinta de papel o verlos a través de la computadora. El médico analiza los pulsos en búsqueda de anomalías y detectar así problemas cardíacos.
La actividad eléctrica del cerebro también se puede registrar con un procedimiento parecido, llamado electroencefalograma.
Una carga Q = − 50.0 nC se localiza a 0.30 m del punto A y a 0.50 m del punto B, tal como se muestra en la figura siguiente. Responder las siguientes preguntas:
a) ¿Cuál es el potencial en A producido por esta carga?
b) Y ¿cuál es el potencial en B?
c) Si una carga q se mueve desde A hasta B, ¿cuál es la diferencia de potencial a través de la cual lo hace?
d) De acuerdo a la respuesta anterior ¿se incrementa su potencial o disminuye?
e) Si q = – 1.0 nC, ¿cuál es el cambio de su energía potencial electrostática mientras se mueve desde A hasta B?
f) ¿Cuánto trabajo hace el campo eléctrico producido por Q mientras la carga de prueba se mueve desde A hasta B?
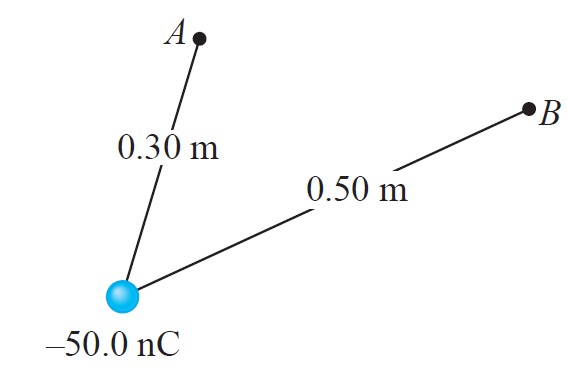
Q es una carga puntual, por lo tanto su potencial eléctrico en A se calcula mediante:
VA = kQ/rA = 9 x 109 x (-50 x 10-9) / 0.3 V = -1500 V
De igual modo
VB = kQ/rB = 9 x 109 x (-50 x 10-9) / 0.5 V = -900 V
ΔV = Vb – Va = -900 – (-1500) V = + 600 V
Si la carga q es positiva su potencial aumenta, pero si es negativa, su potencial disminuye.
ΔV = ΔU/qo → ΔU = qo ΔV = -1.0 x 10-9 x 600 J = -6.0 x 10-7 J.
El signo negativo en ΔU indica que la energía potencial en B es menor que la de A.
Ya que W = -ΔU el campo realiza +6.0 x 10-7 J de trabajo.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 5. Electrostática. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
- Resnick, R. (1999). Física. Vol. 2. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V.
- Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 2. Editorial Reverté.
- Serway, R. Física para Ciencias e Ingeniería. Volumen 2. 7ma. Ed. Cengage Learning.
