Derivadas implícitas: cómo se resuelven y ejercicios resueltos
Las derivadas implícitas son herramientas que se utilizan en una técnica de diferenciación aplicada a funciones. Se aplican cuando no es posible, bajo métodos regulares, realizar el despeje de la variable dependiente que se quiere derivar. Este despeje se realiza en función a la variable independiente.
Por ejemplo, en la expresión 3xy3 – 2y + xy2 = xy, no se puede conseguir la expresión que define a “y” en función de “x”. De manera que al derivar se pueda obtener la expresión diferencial dy/dx.

Índice del artículo
- 1 ¿Cómo se resuelven las derivadas implícitas?
- 2 Regla de la cadena
- 3 Orden operacional
- 4 Implícita de una función
- 5 Historia
- 6 Aplicaciones
- 7 Ejercicios resueltos
- 8 Referencias
Para resolver una derivada implíctia, se parte de una expresión implícita. Por ejemplo: 3xy3 – 2y + xy2 – xy = 0. Esta ya se ha despejado correctamente, sin embargo hacerlo no es una condición necesaria para obtener la derivada de y respecto a x. Después, se deriva cada uno de los elementos respetando la regla de la cadena para funciones mixtas:
3xy3 se compone por 2 variables, por lo tanto d(3xy3) se tratará como la derivada de un producto de funciones.
d(3xy3)/dx = 3y3 + 3y2.(3x) y’ = 3y3 + 9xy2 y’
Donde el elemento y’ se conoce como “y prima” y representa dy/dx
-2y Se deriva según la ley K.U = K.U’
d(-2y) = -2 y’
xy2 supone otro diferencial compuesto por un producto de funciones
d(xy2) = y2 + 2xy y’
-xy se trata de forma homóloga
d(-xy) = -y – x y’
Se sustituyen en la igualdad, conociendo que la derivada de cero es cero.
3y3 + 9xy2 y’ – 2 y’ + y2 + 2xy y’ – y – x y’ = 0
Se agrupan en un lado de la igualdad los elementos que poseen el término y’
3y3 + y2 – y = -9xy2 y’ + 2 y’ + x y’
Se extrae el factor común y’ en el miembro derecho de la igualdad
3y3 + y2 – y = y’ ( -9xy2 + x + 2 )
Por último se despeja el término que multiplica a y’. Obteniéndose así la expresión correspondiente a la derivada implícita de y respecto a x.
y’ = dy/dx = (3y3 + y2 – y)/(-9xy2 + x + 2)
En la derivación implícita se respeta siempre la regla de la cadena. Todas las expresiones diferenciales se darán en función de la variable independiente X. De manera que toda variable θ distinta de X, debe incluir el término dθ/dx después de ser derivada.
Este término aparecerá únicamente en primer grado o con exponente igual a 1. Esta cualidad lo hace completamente despejable bajo métodos tradicionales de factorización. De manera que se hace posible la obtención de la expresión que define al diferencial dθ/dx.
En la regla de la cadena se muestra el carácter progresivo del proceso de diferenciación o derivada. Donde para toda función compuesta f [ g(x) ], se tiene que la expresión diferencial de f será
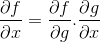
En cada fórmula o ley de derivación que se aplique, se debe tener en cuenta el orden de las variables entre sí. Se respetan los criterios asociados a la variable independiente, sin alterar su correlación con la variable dependiente.
La relación de la variable dependiente al momento de derivar se toma de manera directa.; con la excepción de que se considerará a esta como una segunda función, razón por la cual se aplica el criterio de regla de la cadena para funciones mixtas.
Esto se puede desarrollar en expresiones con más de 2 variables. Bajo los mismos principios se denotarán todos los diferenciales referentes a las variables dependientes.
Gráficamente se maneja el mismo criterio que define a la derivada. Mientras la derivada es la pendiente de la recta tangente a la curva en el plano, el resto de diferenciales pertenecientes a las variables dependientes (dy/dx, dz/dx) representan planos tangentes a los cuerpos vectoriales descritos por las funciones de variable múltiple.
Se dice que una función está implícitamente definida, si la expresión y = f(x) puede representarse como una función de variable múltiple F (x , y) = 0 mientras F esté definido en el plano R2.
3xy3 – 2y + xy2 = xy se puede escribir de la forma 3xy3 – 2y + xy2 – xy = 0
En vista de la imposibilidad de explicitar la función y = f(x).
El cálculo diferencial comenzó a ser nombrado por diversos investigadores matemáticos, alrededor del siglo XVII. La primera vez que se mencionó fue a través de los aportes de Newton y Leibniz. Ambos trataron el cálculo diferencial desde distintos puntos de vista, pero convergiendo en sus resultados.
Mientras Newton se enfocó en la diferenciación como una velocidad o tasa de variación, el enfoque de Leibniz fue más geométrico. Se puede decir que Newton atacó las conjeturas dejadas por Apolonio de Perge y Leibniz las ideas geométricas de Fermat.
La derivación implícita aparece de inmediato al plantearse las ecuaciones diferenciales e integrales. Estas extendieron el concepto geométrico de Leibniz hasta R3 e incluso a espacios multidimensionales.
Las derivadas implícitas se utilizan en diversas situaciones. Son comunes en los problemas de tasa de cambio entre variables relacionadas, donde, según sea el sentido del estudio, se considerarán dependientes o independientes las variables.
También tienen aplicaciones geométricas interesantes, como por ejemplo en problemas de reflexiones o sombras, sobre figuras cuya forma puede modelarse matemáticamente.
Son de frecuente uso en las áreas de economía e ingeniería, así como también en diversas investigaciones de fenómenos naturales y edificaciones experimentales.
Defina la expresión implícita que define a dy/dx
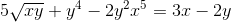
Se diferencia cada elemento de la expresión
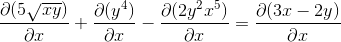
Estableciendo la regla de la cadena en cada caso competente
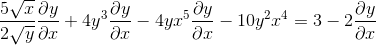
Agrupando en un lado de la igualdad a los elementos que poseen dy/dx
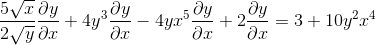
Se factoriza usando el factor común
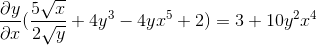
Se despeja obteniendo la expresión buscada
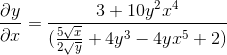
Defina la expresión implícita que define a dy/dx
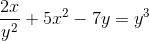
Expresando las derivadas a efectuar
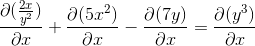
Derivando implícitamente según regla de la cadena
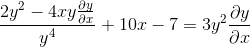
Factorizando elementos comunes
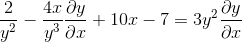
Agrupando el término dy/dx en un lado de la igualdad
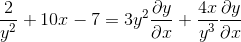
Factor común al elemento diferencial
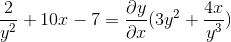
Despejamos y obtenemos la expresión buscada
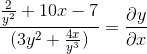
- Calculus of a Single Variable. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 nov. 2008
- The Implicit Function Theorem: History, Theory, and Applications. Steven G. Krantz, Harold R. Parks. Springer Science & Business Media, 9 nov. 2012
- Multivariable Analysis. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 dic. 2010
- System Dynamics: Modeling, Simulation, and Control of Mechatronic Systems. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 mar. 2012
- Calculus: Mathematics and Modeling. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 ene. 1999
