Transformaciones lineales: propiedades, para qué sirven, tipos, ejemplos

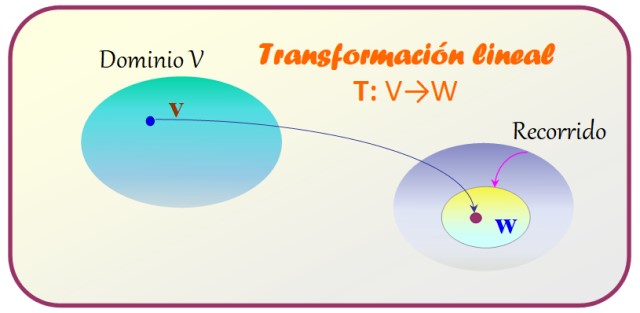
Una transformación lineal, a la que llamaremos simplemente T, relaciona a los elementos de dos espacios vectoriales V y W, asignando a cada vector v perteneciente a V un único vector w que pertenece a W, a través de una operación específica.

Dicha transformación cumple dos condiciones:

-Condición 1

Se refiere a la adición, para que una transformación T sea lineal, tiene que cumplirse que:

T (v + w) = T (v) + T (w)

-Condición 2

La segunda condición representa la homogeneidad en la multiplicación de un escalar por un vector:

T (cv) = c⋅T (v)

La transformación lineal, tal como su nombre lo indica, se encarga de mapear o transformar elementos de V en elementos de W.

La notación para funciones también se utiliza en el caso de las transformaciones lineales, así, el dominio de V es el conjunto de elementos (vectores) a transformar, mientras que el codominio o recorrido es el conjunto resultante.

Un ejemplo de transformación lineal es:

Para indicar que se va a realizar una transformación se usa la letra T. La transformación se va a aplicar a un vector v cuyas componentes son x e y, el cual se ha representado mediante una matriz de una sola columna. El resultado es otro vector w cuyas componentes son x y 0, también representado mediante una matriz columna.

Por lo tanto, esta es una transformación del espacio vectorial R² hacia el espacio vectorial R², que en síntesis se escribe así:

T: R² → R²         

Si tenemos el vector:

La transformación nos devuelve:

Y así con cualquier vector de R². En el ejemplo 1 se comprobará que esta transformación es lineal.

Índice del artículo

• 1 Propiedades de las transformaciones lineales
  • 1.1 Propiedad 1
  • 1.2 Propiedad 2
  • 1.3 Propiedad 3
  • 1.4 Propiedad 4
• 2 Elementos de la transformación lineal
• 3 ¿Para qué sirven las transformaciones lineales?
• 4 Tipos de transformaciones lineales (clasificación)
  • 4.1 Transformaciones lineales sobreyectivas
  • 4.2 Transformaciones lineales biyectivas
  • 4.3 Endomorfismos
  • 4.4 Automorfismos
• 5 Transformaciones lineales especiales
  • 5.1 Operador lineal
  • 5.2 Transformación cero
  • 5.3 Transformación identidad
  • 5.4 Transformación definida por una matriz
  • 5.5 Función lineal
• 6 Aplicaciones
• 7 Ejemplos de transformaciones lineales
  • 7.1 Ejemplo 1
  • 7.2 Ejemplo 2
• 8 Ejercicios resueltos
  • 8.1 – Ejercicio 1
  • 8.2 – Ejercicio 2
• 9 Referencias

Propiedades de las transformaciones lineales

Supongamos una transformación lineal T de V en W, en la cual los vectores v y u pertenecen a V, entonces se cumplen las siguientes propiedades:

Propiedad 1

T (0) = 0

Donde 0 es el vector nulo.

Propiedad 2

T (-v) = – T (v)

Propiedad 3

T (u  – v) = T (u) – T(v)

Propiedad 4

Sea v = c₁v₁ + c₂v₂ + …. +  c_nv_n

 Entonces:

T (c₁v₁ + c₂v₂ + …. +  c_nv_n) = c₁ T(v₁) + c₂ T(v₂) + …. +  c_n T(v_n)

Elementos de la transformación lineal

Sean V y W los ya mencionados espacios vectoriales donde la transformación lineal T transforma elementos de V hacia W. Podemos definir los elementos siguientes:

–Núcleo o kernel de T: es un subconjunto del dominio al que se denota mediante N(T) o ker(T) y comprende todos los elementos de V tales que:

T (v) = 0.

La transformación lineal T (v) = 0 se llama transformación nula.

Naturalmente el vector nulo v = 0 cumple de todas maneras con esta condición, pero el kernel consiste en el conjunto de los vectores no nulos que también la cumplen, para una T dada.

–Imagen de T: es el conjunto de vectores pertenecientes a W tales que son la imagen de por lo menos algún vector en V. Se denota como Im(T) y es subconjunto del espacio vectorial W.

Estos elementos nos servirán para clasificar las transformaciones lineales más adelante.

¿Para qué sirven las transformaciones lineales?

En un principio, las transformaciones lineales trabajan con espacios vectoriales, formados por vectores. Muchas veces asociamos los vectores con fuerzas y otras magnitudes físicas, sin embargo en el procesamiento digital de imágenes, un pixel se puede representar por un vector.

En ese caso, la imagen se puede manipular mediante transformaciones lineales convenientes para obtener los efectos deseados, por ejemplo proyectarse, rotarse, hallar la imagen especular o modificar su tamaño sin cambiar las dimensiones relativas.

Las transformaciones lineales también se usan ampliamente en economía y toma de decisiones, por ejemplo para conocer la cantidad de materia prima requerida para fabricar un determinado lote de productos.

El número de piezas necesario para ensamblar los diversos modelos que produce una fábrica, se pueden trabajar mediante un arreglo matricial, como veremos más adelante.

Tipos de transformaciones lineales (clasificación)

Al igual que las funciones, las transformaciones lineales pueden ser:

-Inyectivas o monomorfismos

-Biyectivas o epimorfismos

-Sobreyectivas o isomorfismos

Además están los siguientes tipos:

-Endomorfismos

-Automorfismos.

Transformaciones lineales inyectivas

Sean V y W espacios  vectoriales y T una transformación lineal T: V → W. T es inyectiva cuando:

Ker (T) = 0

Transformaciones lineales sobreyectivas

Si V y W son  los espacios vectoriales tales que T: V → W, se dice que T es biyectiva cuando:

Im (T) = W

Transformaciones lineales biyectivas

Un transformación lineal T: V → W es biyectiva cuando es a la vez inyectiva y sobreyectiva. Por lo tanto se cumple que:

Ker (T) = 0 e Im (T) = W

Endomorfismos

Son transformaciones lineales en las cuales coinciden el dominio y el codominio.

Automorfismos

Esta clase de transformaciones lineales son endomorfismos biyectivos.

Transformaciones lineales especiales

Operador lineal

Una transformación lineal T: V → V, que va de un espacio vectorial al mismo espacio vectorial se denomina operador lineal.

Transformación cero

Mencionada más arriba, la transformación cero es importante para hallar el kernel de una transformación lineal:

T: V → W tal que T (v) = 0 para cualquier v.

Transformación identidad

T: V → V tal que T (v) = v  para cualquier v.

Transformación definida por una matriz

T: V → W tal que T (v) = Av, donde A es una matriz y v es un vector columna.

Función lineal

Las funciones lineales del tipo y = mx son transformaciones lineales. Tomemos por ejemplo y = 3x y veamos si cumple las dos condiciones del comienzo, probando con dos valores a y b cualesquiera:

f (a+b) = 3 (a+b) = 3a + 3b = f(a)+f(b)

f(ka) = 3(ka) = k⋅(3a) =k⋅f(a)

Efectivamente se trata de una transformación lineal.

Aplicaciones

Las transformaciones lineales tienen aplicaciones matemáticas, como por ejemplo:

-Rotación de ejes coordenados.

-En la solución de sistemas de ecuaciones diferenciales lineales.

-Problemas de autovalores y autovectores.

Y también tienen aplicaciones en otros campos de la ciencia, por ejemplo en mecánica, mecánica cuántica y economía, entre otras áreas.

Ejemplos de transformaciones lineales

Ejemplo 1

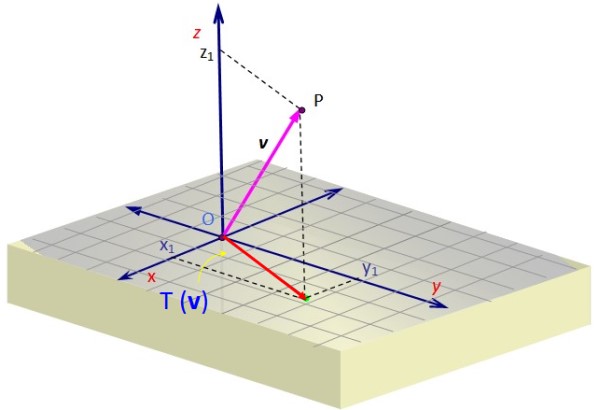
En muchos problemas de Mecánica necesitamos hallar la proyección de un vector v perteneciente al espacio, sobre un determinado plano. Este vector v puede representar por ejemplo una fuerza.

Supongamos que se desea proyectar el vector v = sobre el plano xy. Podemos definir una transformación lineal dada por la siguiente matriz:

Cuando la aplicamos al vector v obtenemos un vector cuya componente z se anula. Geométricamente se representa así, con la proyección de v sobre el plano xy como el vector de color rojo con dos componentes.

Ejemplo 2

Supongamos que se tiene una fábrica que produce tres tipos de carritos de juguete: C1, C2 y C3, para los cuales necesita a su vez tres tipos de piezas en determinadas cantidades para fabricar cada tipo de carrito:

-Ejes o pieza A

-Ruedas o pieza B

-Chasis o pieza C

Para cada tipo de carrito, el número de piezas es diferente, ya que los modelos son distintos. Podemos acomodar las cantidades ordenadamente en una matriz de 3×3, en la cual las columnas están encabezadas por el tipo de carrito, y las filas corresponden a la cantidad de piezas necesarias para elaborar cada modelo.

Este es un ejemplo de transformación dada por una matriz que quedaría así:

Si la fábrica recibe una determinada orden de compra, que consiste en x cantidad de C1, y  de C2 y z de C3, ¿cuántas piezas A, B y C necesita tener disponible para ensamblar los carritos del pedido?

Debemos encontrar una transformación lineal T(x) tal que:

Para obtener el vector Y:

Que nos dará la cantidad de partes que debemos tener en disposición. En el ejercicio resuelto 2 evaluamos la eficacia de las transformaciones lineales para encontrar la cantidad de partes necesaria para cumplir con un determinado pedido.

Ejercicios resueltos

– Ejercicio 1

Comprobar que la siguiente transformación T: R² → R² es lineal:

Solución

Para ello hay que asegurarse de que la transformación cumpla las dos condiciones descritas al comienzo, primero la de adición y luego la del producto de un escalar por un vector. Así que hay que tomar dos vectores v y  u pertenecientes a R², escribiéndolos mediante la notación matricial o especificando las componentes.

Estos vectores son:

v = x₁, y₁

u = x₂, y₂

Primera condición

-Recordando que los vectores se suman componente a componente, se tiene que verificar que:

T (v+u) = T (v) + T (u)

T (v+u) = T (x₁+ x₂ ; y₁ + y₂)

De aquí se obtiene que:

T (x₁+ x₂ ; y₁ + y₂) = (x₁+ x₂; 0)

-Por el otro lado, al aplicar la transformación a cada vector por separado:

T (x₁,y₁) + T (x₂,y₂) = (x₁,0) + (x₂,0)

Al sumar los vectores resultantes se obtiene efectivamente:

w =  (x₁+ x₂; 0)

Como ambos resultados son idénticos, la primera condición se satisface.

Segunda condición

Ahora vamos a comprobar que al multiplicar por un escalar c, este puede salir fuera de la transformación:

T(cv) = c⋅T(v)

Sean:

v = x₁, y₁

c.v = c⋅x₁, c⋅y₁

Entonces:

T(cv) = T (c⋅x₁, c⋅y₁ ) = (c⋅x₁ , 0)

Pero sabemos que del paso anterior que T (v) = T (x₁, y₁ ) =  (x₁ , 0).

Así que como ambas expresiones son idénticas, la segunda condición también se cumple y la transformación es lineal.

– Ejercicio 2

Una fábrica de carritos de juguete ensambla tres modelos de vehículo: C1, C2 y C3, para los cuales necesita las piezas A, B y C que son respectivamente ejes, ruedas y chasis. Las cantidades requeridas se encuentran en la siguiente tabla:

Se le ha pedido a la fábrica que elabore 12 modelos C1, 22 C2 y 16 C3. ¿Cuántas piezas A, B y C se requieren para completar el pedido?

Solución

Se aplica la transformación lineal T(x) = Y, cuyo resultado es el producto entre matrices:

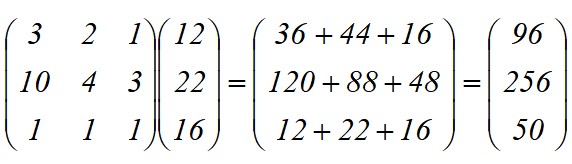
Se requieren en total:

-96 ejes

-256 ruedas

-50 chasis.

Referencias

1. Álgebra y Geometría Analítica. Núcleo e imagen. Clasificación de las transformaciones lineales. Recuperado de: aga.frba.utn.edu.ar.
2. Grossman, S. 2012. Álgebra lineal. 7ma. Edición. McGraw Hill.
3. Gutiérrez, E. 2014. Álgebra lineal y sus aplicaciones. Grupo Editorial Patria.
4. Larson, R. 2016. Fundamentos de Álgebra lineal. 6ta. Edición. Cengage Learning.
5. Wikipedia. Aplicaciones lineales. Recuperado de: es.wikipedia.org.