Aceleración centrípeta: definición, fórmulas, cálculo, ejercicios
La aceleración centrípetaac, también denominada radial o normal, es la aceleración que lleva un objeto móvil cuando describe una trayectoria circular. Su magnitud es v2/r, donde r es el radio del círculo, está dirigida hacia el centro del mismo y es la responsable de que el móvil se mantenga en su recorrido.
Las dimensiones de la aceleración centrípeta son longitud por unidad de tiempo al cuadrado. En el Sistema Internacional son m/s2. Si por alguna razón la aceleración centrípeta desaparece, también lo hace la fuerza que obliga al móvil a mantener la trayectoria circular.

Esto es lo que le sucede a un auto que intenta dar una curva sobre una pista plana y helada, en la que el rozamiento entre el piso y las ruedas es insuficiente para que el coche tome la curva. Por lo tanto la única posibilidad que le queda es la de moverse en línea recta y por eso se sale de la curva.
Índice del artículo
- 1 Los movimientos circulares
- 2 La fuerza centrípeta
- 3 Fórmulas para la aceleración centrípeta
- 4 Ejercicio resuelto
- 5 Referencias
Cuando un objeto se mueve en círculo, en todo momento la aceleración centrípeta está dirigida radialmente hacia el centro de la circunferencia, dirección que es perpendicular a la trayectoria seguida.
Como la velocidad siempre es tangente a la trayectoria, entonces la velocidad y la aceleración centrípeta resultan ser perpendiculares. Por lo tanto la velocidad y la aceleración no siempre tienen la misma dirección.
Bajo estas circunstancias, el móvil tiene la posibilidad de describir la circunferencia con rapidez constante o variable. El primer caso se conoce como Movimiento Circular Uniforme o MCU por sus siglas, el segundo caso será un Movimiento Circular Variable.
En ambos casos, la aceleración centrípeta se encarga de mantener al móvil dando vueltas, ocupándose de que la velocidad varíe únicamente en dirección y en sentido.
Sin embargo, para tener un Movimiento Circular Variable haría falta otra componente de la aceleración en la misma dirección de la velocidad, que se encargue de aumentar o disminuir la celeridad. Esta componente de la aceleración se conoce como aceleración tangencial.
El movimiento circular variable y el movimiento curvilíneo en general poseen ambas componentes de la aceleración, porque el movimiento curvilíneo puede imaginarse como el recorrido por innumerables arcos de circunferencia que componen la trayectoria curva.
Ahora bien, una fuerza se encarga de proporcionar la aceleración. Para un satélite que orbita la tierra, es la fuerza de gravedad. Y puesto que la gravedad actúa siempre perpendicularmente a la trayectoria, no altera la rapidez del satélite.
En tal caso la gravedad actúa como una fuerza centrípeta, que no es una clase especial o aparte de fuerza, sino una que en el caso del satélite, está dirigida radialmente hacia el centro de la tierra.
En otros tipos de movimiento circular, por ejemplo un coche que toma una curva, el rol de la fuerza centrípeta es interpretado por el roce estático y para una piedra atada a una cuerda que se hace girar en círculos, la tensión en la cuerda es la fuerza que obliga al móvil a dar vueltas.
La aceleración centrípeta se calcula mediante la expresión:
ac = v2/r

A continuación se deducirá esta expresión. Por definición la aceleración es la variación de la velocidad en el tiempo:
El móvil emplea un tiempo Δt en el recorrido, el cual es pequeño, puesto que los puntos están muy cercanos.
La figura muestra también dos vectores de posición r1 y r2, cuyo módulo es el mismo: el radio r de la circunferencia. El ángulo entre ambos puntos es Δφ. En verde resalta el arco recorrido por el móvil, denotado como Δl.
En la figura de la derecha se ve que la magnitud de Δv, el cambio en la velocidad, es aproximadamente proporcional a Δl, ya que el ángulo Δφ es pequeño. Pero el cambio en la velocidad está relacionado precisamente con la aceleración. Del triángulo se advierte, por suma de vectores que:
v1 + Δv = v2 → Δv = v2 – v1
Δv es interesante, ya que es proporcional a la aceleración centrípeta. De la figura se advierte que siendo pequeño el ángulo Δφ, el vector Δv es en esencia perpendicular tanto a v1 como a v2 y apunta al centro de la circunferencia.
Aunque hasta aquí los vectores se destacan en negrita, para los efectos de naturaleza geométrica que siguen, se trabaja con los módulos o magnitudes de estos vectores, prescindiendo de la notación vectorial.
Algo más: se necesita hacer uso de la definición de ángulo central, que es:
Δφ= Δl/r
Ahora se comparan ambas figuras, que son proporcionales ya que el ángulo Δφ es común:
Dividiendo entre Δt:
ac=v2/r
Una partícula se mueve en un círculo de 2.70 m de radio. En determinado momento su aceleración es de 1.05 m/s2 en una dirección que hace un ángulo de 32.0º con la dirección de movimiento. Calcule su velocidad:
a) En ese momento
b) 2.00 segundos después, suponiendo aceleración tangencial constante.
Se trata de un movimiento circular variado, puesto que el enunciado indica que la aceleración tiene un ángulo dado con la dirección del movimiento que no es ni 0º (no podría tratarse de un movimiento circular) ni 90º (sería un movimiento circular uniforme).
Por lo tanto las dos componentes -radial y tangencial- coexisten. Se denotarán como ac y at y aparecen dibujadas en la siguiente figura. El vector en verde es el vector aceleración neta o simplemente aceleración a.
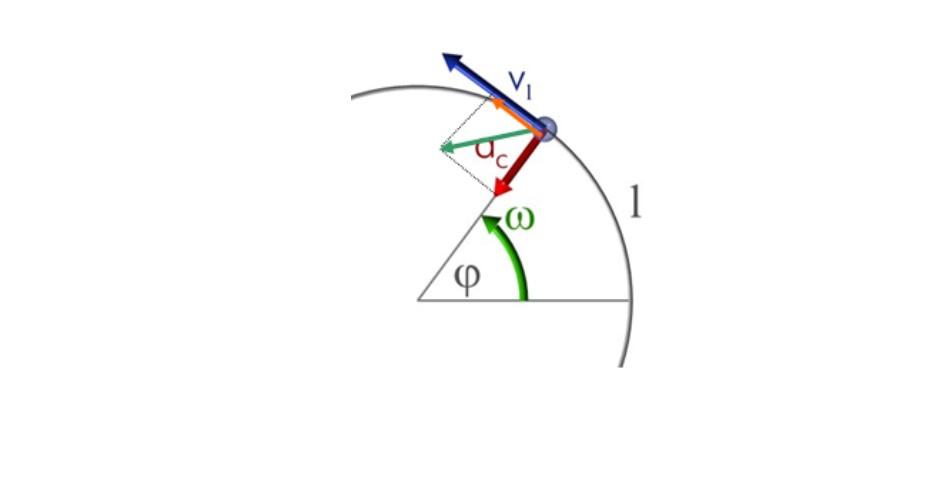
a) Cálculo de las componentes de la aceleración
ac = a.cos θ = 1.05 m/s2 . cos 32.0º = 0.89 m/s2 (en rojo)
at = a.sen θ = 1.05 m/s2 . sen 32.0º = 0.57 m/s2 (en naranja)
Cálculo de la celeridad del móvil
Puesto que ac = v2/r, entonces:
v = vo +at. t = 1.6 m/s + (0.57 x 2) m/s = 2.74 m/s
- Giancoli, D. Physics. 2006. Principles with Applications. Sixth Edition. Prentice Hall. 107- 108.
- Hewitt, Paul. 2012. Conceptual Physical Science. Fifth Edition.Pearson.106 – 108.
