Resta de vectores: método gráfico, ejemplos, ejercicios

La resta de vectores o sustracción vectorial entre los vectores u y v denotada mediante u – v, se calcula sumando el vector u con el vector opuesto a v. Algebraicamente la resta queda expresado así:

u – v = u + (-v)

Es posible llevar a cabo la resta de vectores siguiendo diversos procedimientos, por ejemplo en forma gráfica, de esta manera un vector v se dibuja mediante un segmento de recta orientado –una flecha-.

La longitud de la flecha corresponde al módulo del vector, la inclinación –respecto a una línea de referencia dada- señala la dirección y el extremo señala el sentido del vector.

El vector opuesto a v tiene las mismas longitud y dirección, pero sentido contrario. Entonces, antes de efectuar la resta entre u y v, es preciso dibujar el vector opuesto a v, y sumar este vector a u.

Es muy importante destacar que la resta de vectores no es conmutativa, es decir, el orden de los vectores sí altera el resultado, por lo tanto:

u – v ≠ v – u

El procedimiento gráfico se puede llevar a cabo empleando alguno de estos métodos, cuyos pasos explicaremos seguidamente:

-Método del triángulo.

-Método del paralelogramo.

Índice del artículo

• 1 Método gráfico de resta de vectores
  • 1.1 Método del triángulo
  • 1.2 Método del paralelogramo
• 2 Ejemplos de resta de vectores
  • 2.1 – Ejemplo 1
  • 2.2 – Ejemplo 2
• 3 Ejercicio resuelto
  • 3.1 Solución
• 4 Referencias

Método gráfico de resta de vectores

Método del triángulo

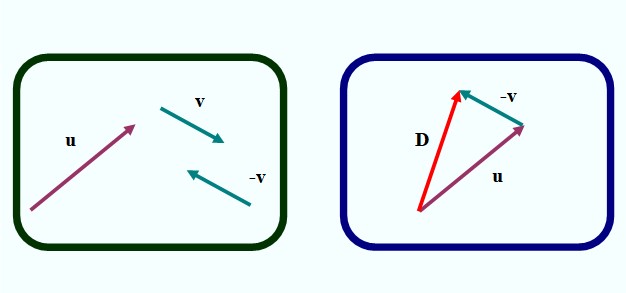
En la figura 1 tenemos el primero de los métodos para restar gráficamente dos vectores. Se trata del método del triángulo, debido a que la figura que se forma al establecer los vectores es un  triángulo, como podemos ver en la imagen izquierda.

Para efectuar la resta u – v procedemos del siguiente modo:

-Dibujar el vector –v a partir del vector v, mediante traslación con regla y escuadra, pero cambiando el sentido de la flecha (imagen izquierda).

-Se traslada al vector –v de tal manera que su origen coincida con  el extremo del vector u (imagen derecha).

-A continuación se dibuja un vector  (en rojo en la imagen derecha) que va desde el origen de u hasta el extremo de v. Lo llamamos D y es el vector diferencia:

D = u – v

Método del paralelogramo

En el método del paralelogramo los vectores a sumar o restar deben coincidir en sus puntos de origen. Supongamos que  queremos hallar u – v con nuestros vectores mostrados anteriormente, los pasos para encontrar la resta de vectores por este método son los siguientes:

-Determinar el vector opuesto a v, que es –v, tal como se describió antes para el método del triángulo.

-Trasladar cuidadosamente los vectores u y –v de tal manera que sus orígenes coincidan.

-Ahora se trazan líneas paralelas segmentadas que parten desde los extremos de cada vector. La figura que se forma es un paralelogramo y en casos especiales en que los vectores sean perpendiculares, resulta un rectángulo o un cuadrado.

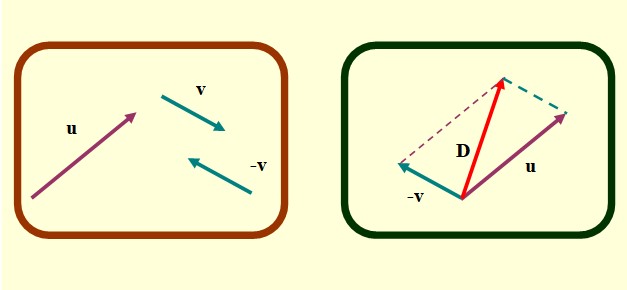
-Finalmente se traza un vector que parte del origen común de u y v hasta el extremo donde se cruzan las líneas paralelas segmentadas. Este es el vector D o sustracción.

Importante

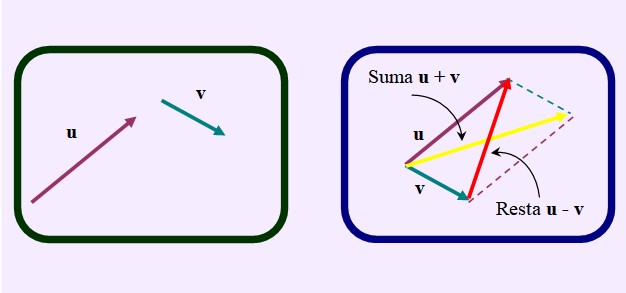
Otra forma de efectuar la resta es dibujar el paralelogramo como si se quisiera sumar los vectores.

Pero en vez de trazar la diagonal habitual de la suma, que va desde el origen común hasta la intersección de las paralelas, se dibuja la diagonal contraria o más corta, como se ve en la figura:

Ejemplos de resta de vectores

– Ejemplo 1

Un barco navega en un río y lo hace en sentido contrario al de la corriente. Un observador en tierra observa que la velocidad del barco se reduce debido a la acción de la corriente.

La velocidad es un vector y en este ejemplo, la velocidad del barco apunta en un sentido y la de la corriente tiene la misma dirección y sentido contrario. La velocidad neta del barco es la suma de ambos vectores.

Por ejemplo, si los instrumentos de la embarcación señalan que se desplaza a v’=+40 km/h y un observador en la orilla mide que el barco se mueve a v=+30 km/h. Como v = v’ +Vc, siendo Vc la velocidad de la corriente que se calcula mediante la resta de las velocidades v y v’ respectivamente: Vc = v – v’ = 30 km/h – 40 km/h = -10 km/h.

– Ejemplo 2

En cinemática tenemos vectores importantes que describen cambios:

-Desplazamiento para los cambios en la posición.

-Velocidad media, para cuantificar qué tan rápido varía la posición en el tiempo.

-Aceleración, para las modificaciones de la velocidad en función del tiempo.

El vector desplazamiento

El vector desplazamiento describe el cambio de posición que experimenta un cuerpo en el transcurso de su movimiento.

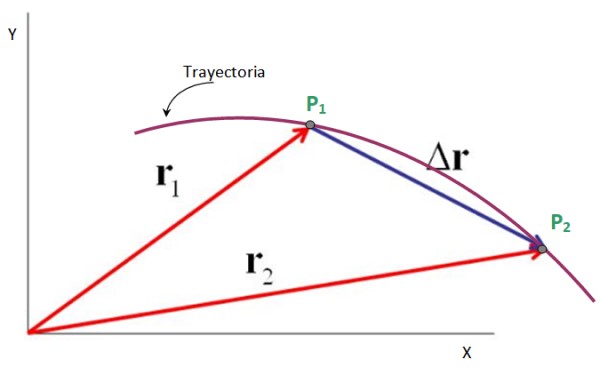
Veamos por ejemplo una partícula que describe la trayectoria plana mostrada en la figura, en la cual pasa del punto P₁ al punto P₂.

Los vectores dirigidos desde el origen del sistema de coordenadas x-y hasta dichos puntos son los vectores de posición r₁ y r₂, mientras que el vector desplazamiento es Δr, que va desde P₁ a P₂. Se cumple que:

Δr = r₂ – r₁

Por lo tanto, el vector desplazamiento es la resta entre el vector de posición final y el vector de posición inicial, tal como se advierte de la siguiente figura. Sus unidades también son las de la posición: metros, pies, millas, centímetros y más.

Los vectores velocidad media y aceleración media

Por su parte, el vector velocidad media v_m se define como el desplazamiento multiplicado por el inverso del intervalo de tiempo:

Ejercicio resuelto

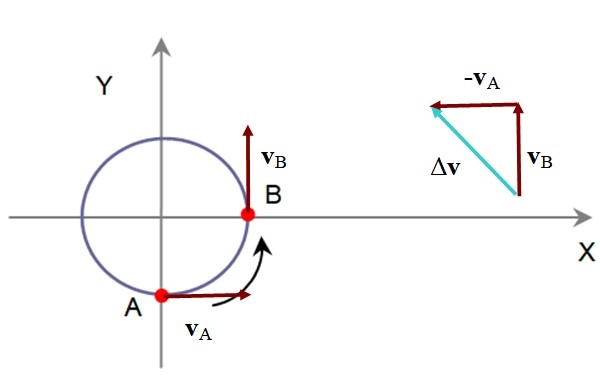
Una partícula que describe una circunferencia tarda 5 s en pasar desde el punto A hasta el punto B. En A tiene una velocidad v_A = 60 km/h hacia el eje +x y en B es v_B = 60 km/h hacia +y. Determinar su aceleración  media en forma gráfica y analítica.

Solución

En forma gráfica, dirección y el sentido de la aceleración media se determinan mediante:

En la siguiente imagen está la resta v_B – v_A, mediante el método del triángulo, ya que la aceleración media a_m es proporcional a Δv. El triángulo formado tiene los dos catetos iguales y por lo tanto los ángulos internos agudos miden 45 º cada uno.

En forma analítica, si la dirección +x coincide con el vector unitario i y la dirección +y con el vector unitario j, entonces:

Δv = 60 km/h j – 60 km/h i

Tomando Δt = 5 s , de acuerdo a la información del enunciado, la aceleración media es:

a_m = (60 km/h j – 60 km/h i) / 5 s = 12 (j–i) km/(h.s)

Referencias

1. Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
2. Bedford, 2000. A. Mecánica para Ingeniería: Estática. Addison Wesley.
3. Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
4. Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
5. Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.
6. Tipler, P. 2006. Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté.