Teorema de Green, demostración, aplicaciones y ejercicios
El teorema de Green es un método de cálculo utilizado para relacionar integrales de línea con integrales dobles de área o superficie. Las funciones implicadas deben estar denotadas como campos vectoriales y definidas dentro de la trayectoria C.
Por ejemplo una expresión de integral de línea puede ser muy complicada de resolver; sin embargo al implementar el teorema de Green, las integrales dobles se vuelven bastante básicas. Es siempre importante respetar el sentido positivo de la trayectoria, esto se refiere al sentido contrario a las agujas del reloj.

El teorema de Green es un caso particular del teorema de Stokes, donde la proyección de la función vectorial se realiza en el plano xy.
Índice del artículo
- 1 Definición
- 2 Demostración
- 3 Aplicaciones
- 4 Historia
- 5 Relación con otros teoremas
- 6 Ejercicios
- 7 Referencias
La expresión del Teorema de Green es la siguiente:
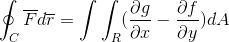
En el primer término se observa la integral de línea definida por la trayectoria “C”, del producto escalar entre la función vectorial “F” y el del vector “r”.
C : Es la trayectoria definida sobre la cual se proyectará la función vectorial siempre y cuando esté definida para ese plano.
F : Función vectorial, donde cada una de sus componentes está definida por una función como tal (f , g).
r : Es un vector tangente a la región R sobre la que se define la integral. En este caso se opera con un diferencial de este vector.
En el segundo término vemos el teorema de Green desarrollado, donde se observa la integral doble definida en la región R de la diferencia de las derivadas parciales de g y f, con respecto a x e y respectivamente. Por un diferencial de área que no es más que el producto de ambos diferenciales bidimensionales (dx.dy).
Este teorema es perfectamente aplicable para el espacio e integrales de superficie.
Para demostrar el teorema de Green de una manera sencilla, esta tarea se desglosará en 2 partes. Primeramente asumiremos que la función vectorial F solo posee definición en el versor i. Mientras la función “g” correspondiente al versor j será igual a cero.
F = f(x,y)i + g(x,y)j = f(x,y)i + 0
r = xi + yj
dr = dxi + dyj
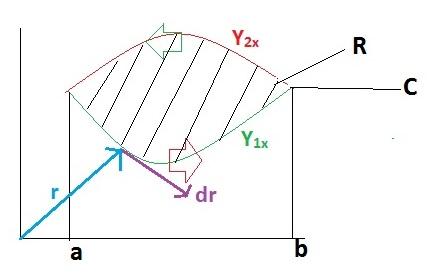
Primero desarrollamos la integral de línea por sobre la trayectoria C, para lo cual se ha sectorizado la trayectoria en 2 tramos que van primeramente desde a hasta b y luego de b hasta a.

Se aplica la definición del teorema fundamental del cálculo para una integral definida.

Se reordena la expresión en una sola integral, se hace factor común al negativo y se invierte el orden de los factores.
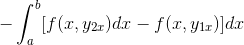
Al observar con detalle esta expresión, se hace evidente que al aplicar los criterios de función primitiva, se está en presencia de la integral de la expresión derivada de f respecto a y. Evaluada en los parámetros
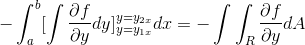
Ahora basta suponer que la función vectorial F está definida únicamente para g(x,y)j. Donde al operar de manera homologa al caso anterior, se obtiene:

Para finalizar, se toman las 2 demostraciones y se unen en el caso donde la función vectorial toma valores para ambos versores. De esta forma se muestra como la integral de línea tras definirse y considerarse como una trayectoria unidimensional, se puede desarrollar completamente para el plano y espacio.
F = f(x,y)i + g(x,y)j
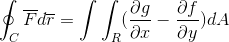
De esta forma queda demostrado el teorema de Green.
Las aplicaciones del teorema de Green son amplias en las ramas de física y matemática. Estas se extienden a cualquier aplicación o uso que se le pueda dar a la integración de línea.
El trabajo mecánico realizado por una fuerza F a través de una trayectoria C, puede ser desarrollado por una integral de línea que se expresa como integral doble de un área mediante el teorema de Green.
Los momentos de inercia de muchos cuerpos sometidos a fuerzas externas en diferentes puntos de aplicación, también responden a integrales de línea desarrollables con el teorema de Green.
Esto tiene múltiples funcionalidades en los estudios de resistencia de materiales bajo uso. Donde los valores externos pueden ser cuantificados y tomados en cuenta previo a la elaboración de diversos elementos.
En general, el teorema de Green facilita la comprensión y definición de las zonas donde las funciones vectoriales están definidas con respecto a una región según una trayectoria.
Fue publicado en 1828 en la obra Mathematical analysis to the theories of electricity and magnetism, escrito por el matemático británico George Green. En ella se exploran apartados bastante determinantes en la aplicación del cálculo en la física, como el concepto funciones de potencial, las funciones de Green y las aplicaciones de su teorema auto titulado.
George Green formalizó su carrera estudiantil a los 40 años, siendo hasta el momento un matemático completamente autodidacta. Tras estudiar en la universidad de Cambridge continuo sus investigaciones, realizando aportes en materia de acústica, óptica e hidrodinámica que siguen vigentes en la actualidad.
El teorema de Green es un caso especial, y surge de otros 2 teoremas muy importantes en la rama del cálculo. Estos son el teorema de Kelvin-Stokes y el teorema de divergencia o de Gauss Ostrogradski.
Partiendo de cualquiera de ambos teoremas se puede llegar al teorema de Green. Ciertas definiciones y proposiciones son necesarias para desarrollar dichas demostraciones.
– En el siguiente ejercicio se muestra cómo transformar una integral de línea en una integral doble respecto a una región R.
La expresión original es la siguiente:
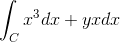

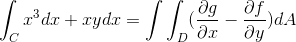
De donde se toman las funciones correspondiente a f y g
f ( x , y ) = x3 g ( x , y ) = yx
df/dy = 0 dg/dx = y

No existe una manera única de definir los límites de integración al aplicar el teorema de Green. Pero sí hay formas donde las integrales luego de ser definidas pueden resultar más simples. De tal forma que la optimización de los límites de integración merece atención.

Donde al resolver las integrales obtenemos:

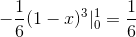
Este valor corresponde en unidades cúbicas a la región debajo de la función vectorial y sobre la región triangular definida por C.
Para el caso de la integral de línea sin efectuar el método de Green, hubiese sido necesario parametrizar las funciones en cada tramo de la región. Esto es, realizar 3 integrales parametrizadas para la resolución. Esto es evidencia suficiente de la eficacia que Robert Green aportó con su teorema al cálculo.
- Introduction to Continuum Mechanics. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23 jul. 2009
- Multivariable Calculus. James Stewart. Cengage Learning, 22 mar. 2011
- An Informal History of Green’s Theorem and Associated Ideas. James Joseph Cross. Department of Mathematics, University of Melbourne, 1975
- Heat Conduction Using Greens Functions. Kevin D. Cole, James V. Beck, A. Haji-Sheikh, Bahman Litkouhi. Taylor & Francis, 16 jul. 2010
- Application of Green’s Theorem to the Extremization of Linear Integrals. Defense Technical Information Center, 1961
