Distancia euclidiana: concepto, fórmula, cálculo, ejemplo
La distancia euclidiana es un número positivo que indica la separación que tienen dos puntos en un espacio donde se cumplen los axiomas y teoremas de la geometría de Euclides.
La distancia entre dos puntos A y B de un espacio euclidiano es la longitud del vector AB perteneciente a la única recta que pasa por dichos puntos.

El espacio que percibimos y donde nos movemos los seres humanos es un espacio tridimensional (3-D), donde se cumplen los axiomas y teoremas de la geometría de Euclides. En este espacio están contenidos subespacios bidimensionales (planos) y subespacios unidimensionales (rectas).
Los espacios euclídeos pueden ser de una dimensión (1-D), de dos dimensiones (2-D), tres dimensiones (3-D) o de n dimensiones (n-D).
Son puntos en el espacio unidimensional X los que pertenecen a la recta orientada (OX), la dirección desde O hacia X es la dirección positiva. Para ubicar los puntos sobre dicha recta se usa el sistema cartesiano que consiste en asignar a cada punto de la recta un número.
Índice del artículo
Se define la distancia euclidiana d(A,B) entre los puntos A y B, ubicados sobre una recta, como la raíz cuadrada del cuadrado de las diferencias de sus coordenadas X:
d(A,B) = √((XB – XA)^2)
Esta definición garantiza que: la distancia entre dos puntos sea siempre una cantidad positiva. Y que la distancia entre A y B sea igual a la distancia entre B y A.
En la figura 1 se muestra el espacio euclidiano unidimensional conformado por la recta (OX) y varios puntos sobre dicha recta. Cada punto tiene una coordenada:
El punto A tiene coordenada XA = 2.5, el B coordenada XB = 4 y el punto C coordenada XC = -2.5
d(A,B) = √((4 – 2.5)2) = 1.5
d(B,A) = √((2.5 – 4)2) = 1.5
d(A,C) = √((-2.5 – 2.5)2) = 5.0
El espacio euclídeo bidimensional es un plano. Los puntos de un plano euclidiano cumplen los axiomas de la geometría de Euclides, por ejemplo:
– Por dos puntos pasa una sola recta.
– Tres puntos sobre el plano forman un triángulo cuyos ángulos internos siempre suman 180º.
– En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de sus catetos.
En dos dimensiones un punto tiene coordenadas X e Y.
Por ejemplo un punto P tiene coordenadas ( XP , YP ) y un punto Q coordenadas ( XQ , YQ ).
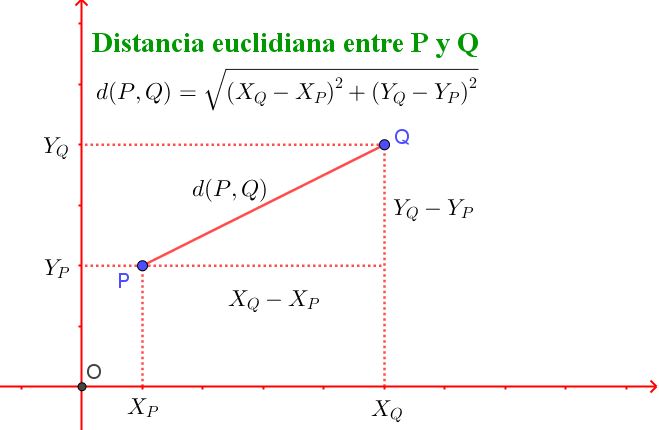
Se define la distancia euclidiana entre el punto P y Q con la siguiente fórmula:
d(P,Q) = √( (XQ – XP)^2 + (YQ – YP)^2 )
Debe notarse que esta fórmula es equivalente al teorema de Pitágoras, tal como lo muestra la figura 2.
No todos los espacios bidimensionales cumplen la geometría euclidiana. La superficie de una esfera es un espacio bidimensional.
Los ángulos de un triángulo sobre una superficie esférica no suman 180º y con ello no se cumple el teorema de Pitágoras, por tanto una superficie esférica no cumple los axiomas de Euclides.
El concepto de coordenadas puede extenderse a dimensiones mayores:
– En 2-D el punto P tiene coordenadas (XP , YP )
– En 3-D un punto Q tiene coordenadas (XQ , YQ, ZQ )
– En 4-D el punto R tendrá coordenadas (XR , YR , ZR , WR )
– En n-D un punto P tendrá coordenadas ( P1 , P2 , P3 , ….. , Pn )
La distancia entre dos puntos P y Q de un espacio euclidiano n-dimensional se calcula con la siguiente fórmula:
d(P,Q) = √( (Q1 – P1)^2 + (Q2 – P2)^2 + …….. + (Qn – Pn)^2 )
El lugar geométrico de todos los puntos Q en un espacio euclidiano n-dimensional que equidistan de otro punto P fijo (el centro) forman una hiperesfera n-dimensional.
A continuación se muestra como se calcula la distancia entre dos puntos ubicados en el espacio tridimensional euclidiano.
Suponga el punto A de coordenadas cartesianas x, y, z dadas por A:( 2, 3, 1) y el punto B de coordenadas B:( -3, 2, 2).
Se quiere determinar la distancia entre estos puntos, para lo cual se hace uso de la relación general:
d(A, B) = √( (-3 – 2)2 + (2 – 3)2 + (2 – 1)2 ) = √( (-5)2 + (-1)2 + (1)2 )
d(A, B) = √( 25 + 1 + 1 ) = √( 27 ) = √( 9 *3 ) = 3 √(3) = 5,196
Se tienen dos puntos P y Q. El punto P de coordenadas cartesianas x, y, z dadas por P:( 2, 3, 1) y el punto Q de coordenadas Q:( -3, 2, 1).
Se pide encontrar las coordenadas del punto medio M del segmento [PQ] que conecta los dos puntos.
Solución:
Se supone que el punto desconocido M tiene coordenadas (X, Y, Z).
Como M es punto medio de [PQ] debe cumplirse que d(P, M) = d(Q, M), por lo que también debe cumplirse d(P, M)^2 = d(Q, M)^2 :
(X – 2)^2 + (Y – 3)^2 + (Z – 1)^2 = (X – (-3))^2 + (Y – 2)^2 + (Z – 1)^2
Como en este caso, el tercer término es igual en los dos miembros la expresión anterior se simplifica a:
(X – 2)^2 + (Y – 3)^2 = (X + 3)^2 + (Y – 2)^2
Se tiene entonces una ecuación con dos incógnitas X e Y. Se requiere de otra ecuación para poder solucionar el problema.
El punto M pertenece a la recta que pasa por los puntos P y Q, la cual podemos calcular de la siguiente manera:
Primero se encuentra el vector director PQ de la recta: PQ = -3-2, 2-3, 1-1> = -5, -1, 0 >.
Luego PM = OP + aPQ, donde OP es el vector posición del punto P y a es un parámetro que pertenece a los números reales.
La ecuación anterior se conoce como ecuación vectorial de la recta, que en coordenadas cartesianas adopta la siguiente forma:
X-2, Y-3, Z-1> = 2, 3, 1> + a -5, -1, 0> = 2 – 5a, 3 – a, 0>
Igualando las componentes correspondientes se tiene:
X – 2 = 2 – 5 a ; Y – 3 = 3 -a ; Z – 1 = 0
Es decir que X = 4 – 5a, Y = 6 – a, por último Z = 1.
Se sustituye en la expresión cuadrática que relaciona X con Y:
(4 – 5a – 2)^2 + (6 – a – 3)^2 = (4 – 5a + 3)^2 + (6 – a – 2)^2
Se simplifica:
(2 – 5a)^2 + (3 -a)^2 = (7 – 5a)^2 + (4 – a)^2
Ahora se desarrolla:
4 + 25 a^2 – 20a + 9 + a^2 – 6a = 49 + 25 a^2 – 70a + 16 + a^2 – 8a
Se simplifica, cancelando términos semejantes en ambos miembros:
4 – 20a + 9 – 6a = 49 – 70a + 16 – 8a
Se despeja el parámetro a:
52 a = 49 + 16 – 4 – 9 = 52 resultando que a = 1.
Es decir que X = 4 – 5, Y = 6 – 1, por último Z = 1.
Finalmente obtenemos las coordenadas cartesianas del punto medio M del segmento [PQ]:
M: (-1, 5, 1).
- Lehmann C. (1972) Geometría analítica. UTEHA.
- Superprof. Distancia entre dos puntos. Recuperado de: superprof.es
- UNAM. Distancia entre variedades sublineales afines. Recuperado de: prometeo.matem.unam.mx/
- wikipedia. Distancia euclidiana. Recuperado de: es.wikipedia.com
- wikipedia. Espacio euclídeo. Recuperado de: es.wikipedia.com
