Leyes de Gossen: explicación con ejemplos
Las leyes de Gossen, creadas por el economista alemán Hermann Gossen (1810-1858), son tres leyes relevantes de la economía relacionadas con la disminución de la utilidad marginal, el coste de adquisición marginal y la escasez.
Gossen fue el primero en explicar la ley de disminución de la utilidad marginal, o primera ley de Gossen, basada en observaciones generales del comportamiento humano. Esta ley afirma que la cantidad de un mismo disfrute disminuye continuamente a medida que se avanza sin interrupción en ese disfrute, hasta alcanzar la satisfacción.

La segunda ley, la ley de utilidad equi-marginal, explica el comportamiento del consumidor cuando tiene recursos limitados, pero deseos ilimitados.
El problema fundamental en una economía es que los deseos humanos son ilimitados, pero no hay recursos adecuados para satisfacer todos los deseos humanos. Por tanto, un individuo racional intenta optimizar los escasos recursos disponibles para alcanzar su máxima satisfacción.
La tercera ley se refiere al valor económico de los productos, el cual resulta de una escasez previa.
Gossen se esforzó por encontrar cada una de estas leyes en todo tipo de actividades económicas.
Índice del artículo
Se conoce como ley de disminución de la utilidad marginal. Establece que cuando un individuo consume más de un producto, la utilidad total aumenta a una tasa decreciente.
Sin embargo, después de cierta etapa, la utilidad total también comienza a disminuir y la utilidad marginal se vuelve negativa. Esto significa que el individuo no necesita más el producto.
Es decir, el deseo de un individuo por un producto en particular se satura cuando lo consume más y más.
Supongamos que se tiene hambre y se poseen algunas naranjas. Comer la primera naranja proporciona una gran cantidad de utilidad. La utilidad marginal de la segunda naranja es ciertamente menor que la de la primera.
Similarmente, la utilidad marginal de la tercera naranja es menor que la de la segunda, y así sucesivamente.
Después de cierta etapa, la utilidad marginal se hace cero y más allá de esta etapa, se vuelve negativa. Esto se debe a que se va saciando a medida que se consumen más y más naranjas.
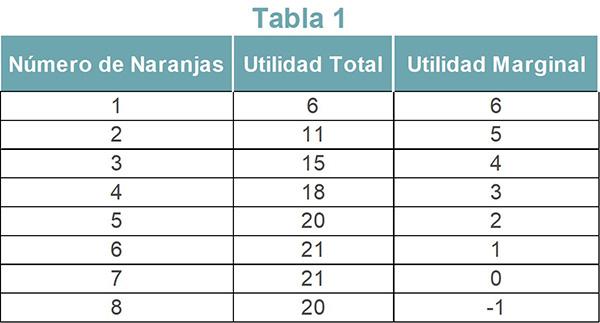
Para comprenderlo mejor, se puede ver la tabla 1. Las cifras son hipotéticas y representan la utilidad marginal del consumo de naranjas para una persona.
Utilidad total
La utilidad total se obtiene al sumar la utilidad marginal de cada unidad consumida de naranja. Según la Tabla 1, la utilidad total de las seis primeras naranjas es 21 (21=6+5+4+3+2+1).
Utilidad marginal
La utilidad marginal de la unidad n-ésima del producto es la diferencia entre la utilidad total de la unidad n-ésima y la utilidad total de la unidad (n-1)-ésima del producto. UMn = UTn – UT(n-1) donde,
UMn= utilidad marginal de la unidad n-ésima.
UTn= Utilidad total de la unidad n-ésima.
UT(n-1)= Utilidad total de la unidad (n-1)-ésima.
En el ejemplo de la Tabla 1, la utilidad marginal de la cuarta naranja es UM4= UT4-UT3= 18-15= 3.
La siguiente figura detalla las trayectorias de las curvas de utilidad total y de utilidad marginal.
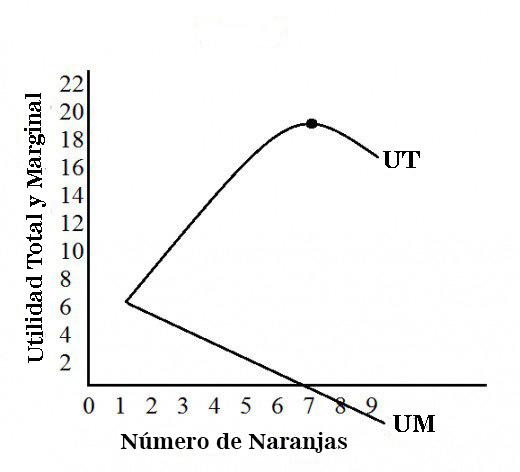
La curva de utilidad total aumenta inicialmente y, luego de cierta etapa, comienza a disminuir. En esta etapa es cuando la curva de utilidad marginal entra en la zona negativa.
La segunda ley dice que cada persona gastará su dinero en diferentes productos, de manera que sea igual la cantidad de todos los placeres.
De este modo, Gossen explicaba que se lograría el máximo disfrute a partir de un nivel uniforme de satisfacción. La segunda ley de Gossen se conoce como la ley de la utilidad equi-marginal.
Supongamos que una persona posee $200. La ley explica cómo la persona asigna los $200 entre sus diferentes deseos para maximizar su satisfacción.
El punto en el que la satisfacción del consumidor es máxima con los recursos dados se conoce como equilibrio del consumidor.
Supongamos que hay dos productos X e Y. El recurso del consumidor es $8. El precio unitario del producto X es $1. El precio unitario del producto Y es $1.
El consumidor gasta sus $8 comprando el producto X. Dado que el precio unitario del producto X es $1, puede comprar 8 unidades.
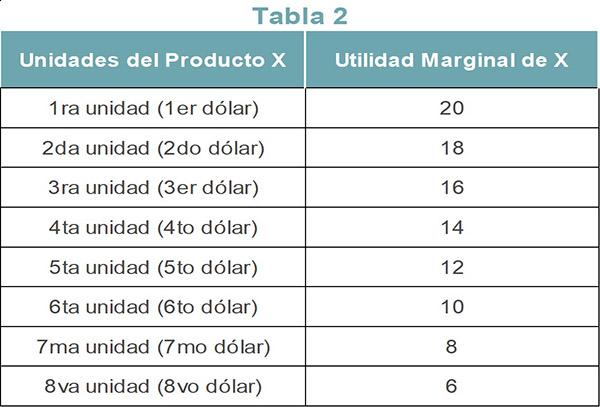
La tabla 2 muestra la utilidad marginal de cada unidad del producto X. Dado que la ley se basa en el concepto de disminución de la utilidad marginal, esta disminuye con cada unidad subsiguiente.
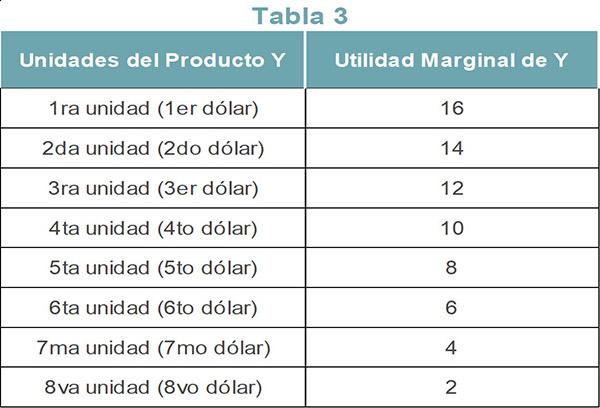
Consideremos ahora que el consumidor gasta sus $8 comprando el producto Y. La tabla 3 muestra la utilidad marginal de cada unidad del producto Y.
Si el consumidor planea asignar sus $8 entre el producto X y el Y, la tabla 4 muestra cómo el consumidor gasta sus ingresos en ambos productos.
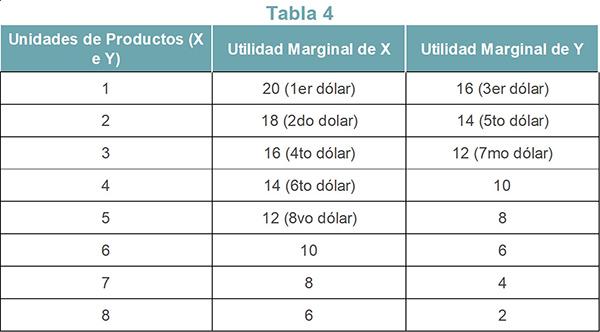
Aplicación de la segunda ley
Dado que la primera unidad del producto X da la mayor utilidad (20), gasta el primer dólar en X. El segundo dólar también se destina al producto X, ya que otorga 18, la segunda más alta.
Tanto la primera unidad del producto Y como la tercera unidad del producto X ofrecen la misma cantidad de utilidad. El consumidor prefiere comprar el producto Y, porque ya ha gastado dos dólares en el producto X.
Del mismo modo, el cuarto dólar lo gasta en X, el quinto dólar en Y, el sexto dólar en X, el séptimo dólar en Y, y el octavo dólar en X.
Así, el consumidor compra 5 unidades del producto X y 3 unidades del producto Y. Es decir, 5 unidades del producto X y 3 unidades del producto Y lo dejan con la mejor cantidad de utilidad total.
De acuerdo con la ley de utilidad equi-marginal, el consumidor está en equilibrio en este punto, experimentando la máxima satisfacción. Para entender esto se puede calcular la utilidad total de los productos consumidos.
Utilidad total= UTx+UTy= (20+18+16+14+12) + (16+14+12) =122. Cualquier otra combinación de productos dejaría al cliente con una menor utilidad total.
Esta ley indica que la escasez es una condición previa necesaria para que exista el valor económico. Es decir, un producto tiene valor solo cuando su demanda excede a su oferta.
Usando la lógica de Gossen, dado que la utilidad marginal disminuye con el consumo, un producto solo podrá tener una utilidad marginal positiva o “valor” si el suministro disponible es menor que el necesario para generar saciedad. De lo contrario, el deseo será saciado y, por tanto, su valor será cero.
Los argumentos de Gossen sobre el valor se basan en las dos leyes anteriores. Según él, el valor es un término relativo. Depende de la relación entre el objeto y el sujeto.
Al aumentar la cantidad, el valor de cada unidad agregada disminuye, hasta que se convierte en cero.
- Kirti Shailes (2018). Gossen’s First and Second Law of Human Enjoyment. Economics Discussion. Tomado de: economicsdiscussion.net.
- Sundaram Ponnusamy (2014). The Law of Diminishing Marginal Utility or Gossen’s First Law. Owlcation. Tomado de: owlcation.com.
- Sundaram Ponnusamy (2016). The Law of Equi-Marginal Utility or Gossen’s Second Law. Owlcation. Tomado de: owlcation.com.
- Economics Concepts (2015). Law of Diminishing Marginal Utility. Tomado de: economicsconcepts.com.
- Wikipedia, the free encyclopedia (2018). Gossen’s laws. Tomado de: en.wikipedia.org.
