Romboide: características, cómo sacar el perímetro y área
Un romboide es una figura plana de cuatro lados, -un cuadrilátero-, en el que sus lados y sus ángulos internos son distintos dos a dos. Por ello el romboide pertenece al grupo de los paralelogramos oblicuos.
Las figuras geométricas forman parte de la naturaleza y en particular las de cuatro lados como el romboide, tienen muchas aplicaciones en la arquitectura y el diseño.

Arriba lo tenemos formando parte de la fachada del estadio de fútbol Allianz Arena en Munich. Son paneles romboidales que se iluminan con los colores del equipo local.
Se trata pues de una figura con mucho dinamismo visual, pues a diferencia de otros cuadriláteros, no tiene eje de simetría. En la siguiente figura se muestran diversos romboides con variadas orientaciones en el plano.
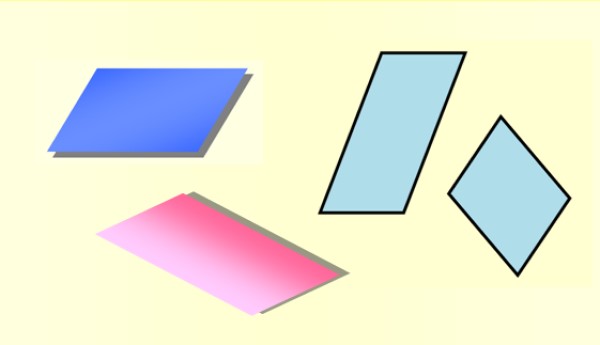
Índice del artículo
Características del romboide
A continuación, las características principales de esta interesante figura geométrica:
-Número de lados: 4.
-Cantidad de vértices: 4.
-Los lados opuestos son iguales y paralelos, en cambio los lados contiguos son desiguales.
-Tiene 4 ángulos internos: dos agudos (menores de 90º), denotados mediante la letra griega α y dos obtusos (mayores de 180º), llamados β (ver figura 3).
-Al sumar dos ángulos contiguos del romboide se obtiene 180º, por lo tanto α y β son suplementarios.
-La suma de los 4 ángulos internos es igual a 360º.
-Una diagonal es un segmento que parte de un vértice y termina en el vértice opuesto.
-El punto en el cual las diagonales del romboide se intersectan se denomina baricentro.
-Las diagonales del romboide tienen tamaños distintos.
Acerca de las diagonales del romboide hay algunos detalles importantes que discutiremos a continuación.
Es muy importante destacar que las diagonales de los romboides no son bisectrices, es decir, no dividen a los ángulos internos de la figura en dos partes iguales.
Las diagonales tampoco son perpendiculares entre sí. Sin embargo, podemos calcularlas fácilmente con el teorema del coseno. Así, la diagonal mayor DM en el romboide de la figura 3 es:
DM = √ (a2 + b2 – 2.ab.cos β)
Y la diagonal menor Dm sería:
Dm = √ (a2 + b2 – 2.ab.cos α)
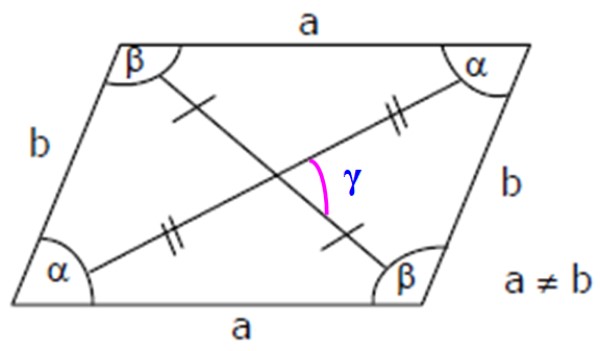
Importante: como α y β son suplementarios, se cumple que:
sen α = sen β
cos α = -cos β
Estas propiedades de las razones trigonométricas hay que tenerlas en cuenta al momento de resolver los ejercicios.
Cómo sacar el perímetro y el área
Para encontrar el perímetro y el área vamos a darle nombre a los lados del romboide, estos serán a y b. Además tenemos la altura del romboide, llamada h, que es la línea dibujada desde uno de los vértices y dirigida perpendicularmente hacia el lado opuesto de la figura.
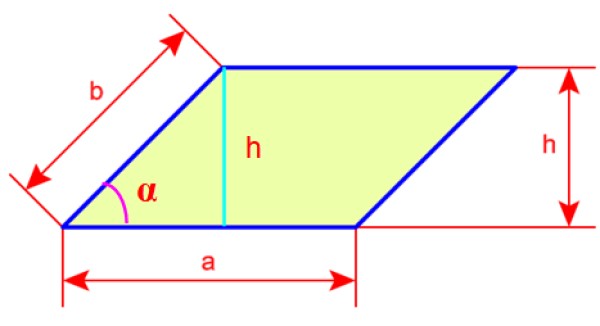
El perímetro del romboide se calcula sumando las longitudes de sus cuatro lados. Llamemos P al perímetro, entonces:
P = 2a + 2b
También lo podemos expresar a través de:
P = 2 (a+b)
Perímetro conociendo la altura
Si nos fijamos bien, la altura h se puede determinar a partir del triángulo de la izquierda en la figura 4. El lado b sería la hipotenusa y la altura h el cateto opuesto al ángulo α, por lo tanto:
sen α = cateto opuesto / hipotenusa
O bien:
sen α = h / b
Entonces despejamos b:
b = h / sen α
Sustituimos en el perímetro P:
P = 2 [a + (h / sen α)]
El área del romboide es la medida de su superficie. Y ya que es un paralelogramo, su área A viene dada por la conocida expresión:
A = base x altura
Que según las figuras 3 y 4 se expresa mediante:
A = a x h
Área conociendo los dos lados y un ángulo interno
Aplicando la trigonometría básica del apartado anterior, encontramos expresiones equivalentes para el área del romboide:
h = b. sen α
Entonces el área queda así:
A = a. b. sen α
Recordando lo que dijimos arriba acerca de los ángulos suplementarios, podemos sustituir sen α por sen β de ser necesario.
Área conociendo las diagonales y el ángulo entre ellas
Finalmente, si conocemos las diagonales DM y Dm, más el ángulo γ entre ellas (ver figura 3), el área se puede calcular mediante el semiproducto de las diagonales por el seno de dicho ángulo:
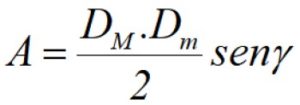
En el siguiente romboide, cuyas dimensiones se dan en unidades arbitrarias u.a., encontrar:
a) El valor del perímetro
b) El área
c) Los ángulos internos α y β
d) La longitud del segmento RX
e) La medida de cada una de las diagonales
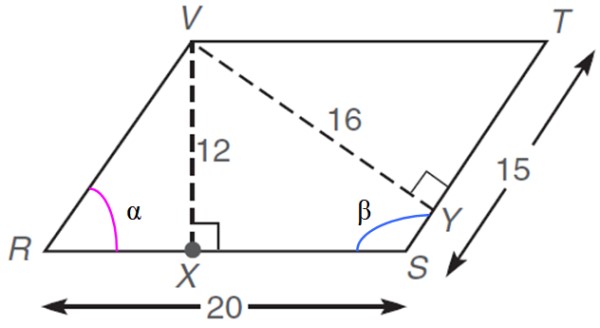
El perímetro P es:
P = 2 (a + b)
Identificamos primer los valores de a y b:
a = 20
b = 15
Sustituimos en la fórmula y calculamos:
P = 2. (20 + 15) = 70 u.a.
El diagrama proporciona la altura h = 12 u.a, por lo tanto el área se puede calcular con la fórmula:
A = a x h
A = 20 x 12 u.a.2 = 240 u.a.2
Sin importar la unidad seleccionada para medir los lados y la altura, el área siempre se expresa en unidades al cuadrado.
El mismo resultado si obtiene al calcular el área con la otra altura del romboide, que vale 16 u.a. En efecto:
A = 16 x 15 u.a.2 = 240 u.a.2
El ángulo α se puede calcular a través de:
h = b. sen α
Ya que se conocen los valores de h y b, por lo tanto:
α = arcsen (h/b) = arcsen (12/15) = 53.13º
Recordando que los ángulos α y β son suplementarios, se cumple:
α + β = 180º ⇒ β = 180 – 53.13º = 126.87º
La longitud sel segmento RX se calcula fácilmente, porque hay bastante información para hallarlo. Por ejemplo mediante:
RX= RV . cos α = 15 . cos 53.13º u.a. = 9 u.a.
También a través del teorema de Pitágoras a través del triángulo rectángulo de lados 15 y 12 u.a:
(RV)2 = (RX)2 + h2
Despejando la longitud del segmento de interés:
RX = √ [(RV)2 – h2] = √ [152 – 122] = √81 = 9
La medida de una de las diagonales, por ejemplo la diagonal que une a los vértices R y T, que es una diagonal mayor, viene dada por el teorema del coseno, como se explicó previamente, así que sustituimos valores allí:
DM = √ (202 + 252 – 2. 20. 15 .cos 126.87º) = 37.22 u.a.
Para la diagonal menor:
Dm = √ (202 + 252 – 2. 20. 15 .cos 53.13º) = 25.79 u.a.
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- Baldor, A. 1973. Geometría y trigonometría. Editorial Cultural Centroamericana.
- E. A. 2003. Elementos de geometría: con ejercicios y geometría del compás. Universidad De Medellín.
- Jiménez, R. 2010. Matemáticas II. Geometría y Trigonometría. Segunda edición. Prentice Hall.
- Polígonos regulares. Recuperado de: mate.ingenieria.usac.edu.gt.
- Universo Fórmulas. Romboide. Recuperado de: universoformulas.com.
- Wikipedia. Romboide. Recuperado de: es.wikipedia.org.
