Vectores equipolentes: definición, notación, ejercicios
Dos o más vectores son equipolentes si tienen el mismo módulo, la misma dirección e igual sentido, aun cuando su punto de origen sea diferente. Recuérdese que las características de un vector son precisamente: origen, módulo, dirección y sentido.
Los vectores se representan mediante un segmento orientado o flecha. En la figura 1 se muestra la representación de varios vectores en el plano, algunos de los cuales son equipolentes según la definición dada inicialmente.
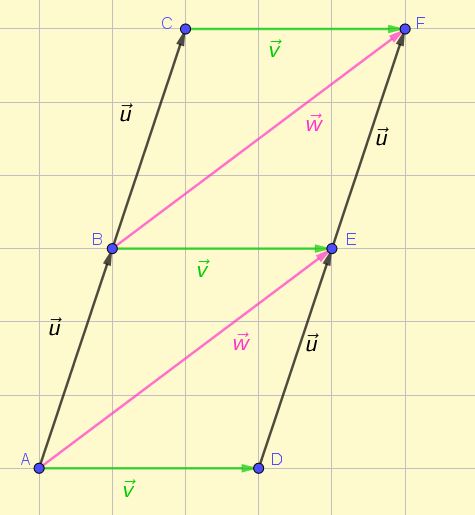
De un primer vistazo es posible apreciar que los tres vectores de color verde tienen el mismo tamaño, la misma dirección y el mismo sentido. Se puede afirmar lo mismo sobre los dos vectores de color rosa y los cuatro vectores negros.
Numerosas magnitudes de la naturaleza tienen un comportamiento de tipo vectorial, tal es el caso de la velocidad, la aceleración y la fuerza, por nombrar solamente algunas. De allí la importancia de caracterizarlos adecuadamente.
Índice del artículo
Para distinguir las cantidades vectoriales de las cantidades escalares frecuentemente se usa la letra de tipo negrita o una flecha sobre la letra. Cuando se trabaja con vectores a mano, sobre el cuaderno, es preciso distinguirlos con la flecha y cuando se usa un medio impreso, se emplean las negritas.
Los vectores pueden denotarse indicando su punto de partida u origen y su punto de llegada. Por ejemplo AB, BC, DE y EF de la figura 1 son vectores, en cambio AB, BC, DE y EF son cantidades escalares o números que indican la magnitud, módulo o tamaño de sus respectivos vectores.
Para indicar que dos vectores son equipolentes se usa el símbolo “∼ “. Con esta notación, en la figura podemos señalar los siguientes vectores que son equipolentes entre sí:
AB∼BC∼DE∼EF
Todos ellos tienen la misma magnitud, dirección y sentido. Cumplen por lo tanto con la normativa que se indicó anteriormente.
Cualquiera de los vectores de la figura (por ejemplo AB) es representante del conjunto de todos los vectores fijos equipolentes. Este conjunto infinito define la clase de vectores libres u.
u = {AB, BC, DE, EF, . . . . .}
Una notación alternativa es la siguiente:
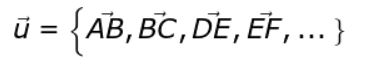
Si no se coloca la negrita o la flechita encima la letra u, es que nos queremos referir al módulo del vector u.
Los vectores libres no están aplicados a algún punto particular.
Por su parte los vectores deslizantes son vectores equipolentes a un vector dado, pero su punto de aplicación debe estar contenido en la recta de acción del vector dado.
Y los vectores opuestos son vectores que tienen igual magnitud y dirección pero sentidos contrarios, aunque en los textos en inglés se les llama de direcciones contrarias ya que la dirección también indica el sentido. Los vectores opuestos no son equipolentes.
¿Cuáles otros vectores de los mostrados en la figura 1 son equipolentes entre sí?
Solución
Aparte de los ya señalados en la sección anterior, se observa a partir de la figura 1 que AD, BE y CE también son vectores equipolentes entre sí:
AD ∼ BE ∼ CE
Cualquiera de ellos es representante de la clase de vectores libres v.
También son equipolentes entre sí los vectores AE y BF :
AE ∼BF
Que son representantes de la clase w.
Los puntos A, B y C están sobre el plano cartesiano XY y sus coordenadas son:
A=(-4,1), B=(-1,4) y C=(-4,-3)
Encuentre las coordenadas de un cuarto punto D de modo tal que los vectores AB y CD sean equipolentes.
Solución
Para que CD sea equipolente a AB debe tener el mismo módulo y la misma dirección que AB .
El módulo de AB elevado al cuadrado es:
|AB|^2 = (-1 – (-4))^2 + (4 -1)^2 = 9 + 9 = 18
Las coordenadas de D son desconocidas por lo que podemos decir: D = (x, y)
Entonces: |CD|^2 = (x -(-4))^2 + (y – (-3))^2
Como |AB|=|CD| es una de las condiciones para que AB y CD sean equipolentes se tiene:
(x + 4)^2 + (y + 3)^2 = 18
Ya que se tienen dos incógnitas se requiere de otra ecuación, la cual puede conseguirse de la condición que AB y CD sean paralelos y en el mismo sentido.
Pendiente del vector AB
La pendiente del vector AB indica su dirección:
Pendiente AB = (4 -1)/(-1 – (-4)) = 3/3 = 1
Indicando que el vector AB forma 45º con el eje X.
Pendiente del vector CD
La pendiente de CD se calcula de forma similar:
Pendiente CD = (y – (-3))/(x -(-4)) = (y + 3)/(x + 4)
Igualando este resultado con la pendiente de AB se tiene la siguiente ecuación:
y + 3 = x + 4
Lo que significa que y = x + 1.
Si este resultado se sustituye en la ecuación de la igualdad de los módulos se tiene:
(x + 4)^2 + (x + 1 + 3)^2 = 18
Simplificando queda:
2 (x+4)^2 = 18,
Que equivale a:
(x+4)^2 = 9
Es decir x+4 = 3 lo que implica que x = -1. De modo que las coordenadas de D son (-1, 0).
Verificación
Las componentes del vector AB son (-1-(-4) ; 4 -1) = (3 ; 3)
y las del vector CD son (-1 -(-4)) ; 0 -(-3)) = (3 ; 3)
Lo que significa que los vectores son equipolentes. Si dos vectores tienen iguales componentes cartesianas tienen igual módulo y dirección, por tanto son equipolentes.
El vector libre u tiene magnitud 5 y dirección 143,1301º.
Encuentre sus componentes cartesianas y determine las coordenadas de los puntos B y C sabiendo que los vectores fijos AB y CD son equipolentes a u. Las coordenadas de A son ( 0, 0 ) y las coordenadas del punto C son (-3,2).
Solución
La situación que plantea el ejercicio puede representarse por la siguiente figura:
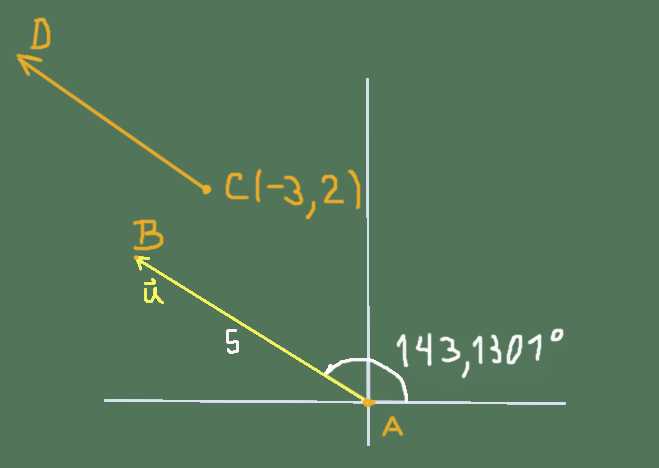
Las componentes cartesianas de u son
u = ( 5*cos(143,1301º) ; 5*sen(143,1301º) )
Haciendo los cálculos queda:
u = ( -4 ; 3 )
Las coordenadas de B son desconocidas por lo que colocaremos B(x,y)
Las coordenadas del vector AB son (x-0 ; y-0), pero como es equipolente con u debe cumplirse la igualdad de componentes, se concluye por tanto que las coordenadas de B son (-4, 3).
De modo semejante las coordenadas del vector CD son (x-(-3)) ; (y – 2) que debe ser equipolente a u, lo que conduce a:
x + 3 = -4 y y -2 = 3
Entonces las coordenadas del punto D serán (-7, 5).
- Cálculo.cc. Vector fijo. Vector libre. Recuperado de: calculo.cc
- Descartes 2d. Vectores fijos y Vectores libres del plano. Recuperado de: recursostic.educacion.es
- Proyecto Guao. Vectores equipolentes. Recuperado de: guao.org
- Resnick,R., Krane, K. (2001). Physics (en inglés). Nueva York: John Wiley & Sons.
- Serway, R.; Jewett, John W. (2004). Physics for Scientists and Engineers (en inglés) (6ª edición). Brooks/Cole.
- Tipler, Paul A. (2000). Física para la Ciencia y la Tecnología. Volumen I. Barcelona: Ed. Reverté.
- Weisstein, E. “Vector”. En Weisstein, Eric W. MathWorld (en inglés). Wolfram Research.
