Lados homólogos: concepto, explicación, ejemplos, ejercicios

¿Qué son los lados homólogos?

Los lados homólogos en dos figuras geométricas planas son los que se corresponden entre sí, guardando semejanza. Por ejemplo, la mano derecha de una persona es homóloga con la mano derecha de otra persona.

En geometría plana, no solo hay lados homólogos, sino vértices y ángulos homólogos también. Para verlo, considérese la siguiente figura, que consiste en dos triángulos idénticos ABC y A’B’C’:

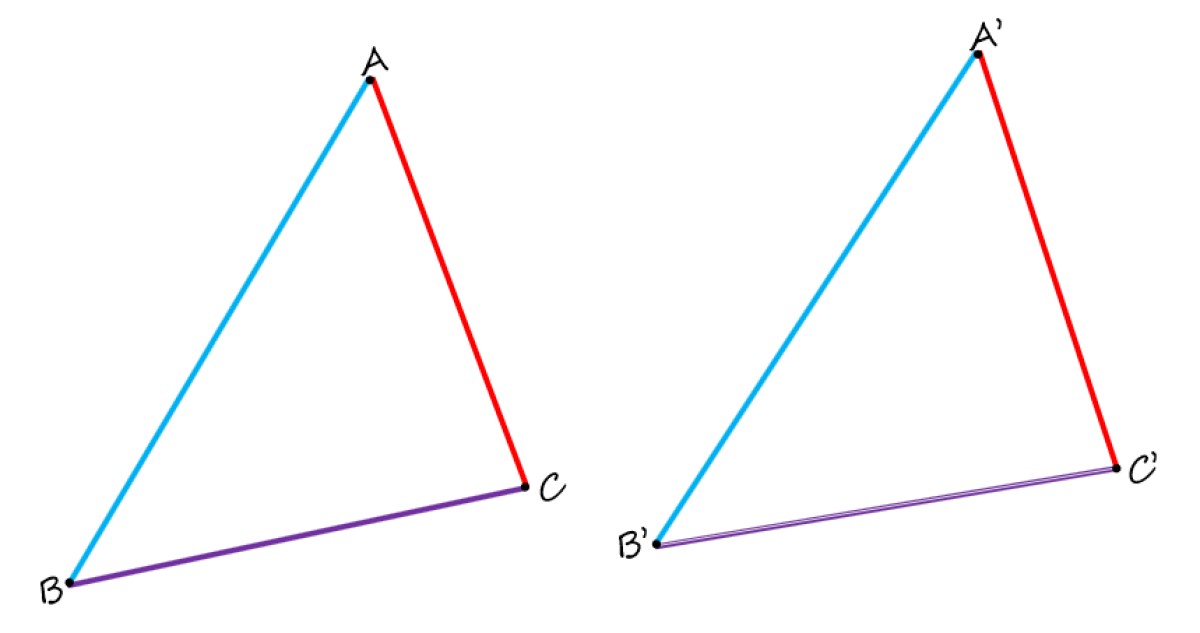
Al compararlos, se observa claramente que los lados AB y A’B’ en color azul son homólogos, pues ocupan una posición semejante en cada triángulo. Los lados BC y B’C’ en morado también son homólogos. Y, por último, el lado AC en color rojo es homólogo al lado A’C’.

Explicación

De lo antes dicho, se desprende que los lados homólogos son aquellos que ocupan la misma posición relativa en figuras de igual forma. En la imagen anterior se utilizaron dos triángulos idénticos para mostrar la idea, pero esta se puede generalizar fácilmente a otras figuras geométricas planas, formadas por lados consecutivos que se cierran.

Estas figuras se denominan polígonos. Por ejemplo, los triángulos y los cuadriláteros son polígonos de 3 y 4 lados respectivamente.

El concepto de lados homólogos es importante porque permite definir criterios de semejanza entre polígonos, como se verá en breve. Las figuras semejantes, tienen exactamente la misma forma y guardan idéntica proporción entre sus lados, aunque no sean del mismo tamaño.

Y aunque hasta ahora se hizo referencia solo a figuras planas, también hay figuras semejantes en tres dimensiones. Se observan fácilmente en los anaqueles de los supermercados, cuando un mismo producto es vendido en envases idénticos, pero con distinto tamaño.

Otras palabras que se utilizan indistintamente en geometría para referirse a los lados homólogos en figuras geométricas son: lados correspondientes, lados respectivos y lados equivalentes.

Vértices y ángulos homólogos

Al igual que con los lados, se definen asimismo los vértices homólogos, que unen pares de lados homólogos. Por ejemplo, los vértices A y A’ de la figura anterior son homólogos. De igual manera, son homólogos los pares de vértices B y B’ y C y C’.

Por último, los ángulos homólogos ocupan la misma posición relativa en las figuras. Los vértices de los ángulos homólogos, son a su vez homólogos.

Para ilustrar la idea, tómese el ángulo entre los lados azul y morado del triángulo izquierdo, que se puede denotar como ∠ABC. Este ángulo tiene su homólogo en el ángulo ∠A’B’C’, del triángulo a la derecha.

El vértice de este ángulo es B, que como se indicó previamente, es homólogo con B’, y los otros dos pares de ángulos homólogos de los triángulos mostrados son:

• ∠BCA y ∠B’C’A’
• ∠CAB y ∠C’A’B’

Semejanza de polígonos

Para que dos polígonos cualesquiera sean semejantes, se deben cumplir las siguientes condiciones:

• Todos los pares de ángulos homólogos tienen la misma medida
• Sus pares de lados homólogos son proporcionales.

Las dos condiciones se deben cumplir simultáneamente para asegurar la semejanza. De inmediato se observa por qué.

En la siguiente figura hay dos cuadriláteros que evidentemente no son semejantes. Se debe a que la primera condición de semajanza se cumple, pero la segunda no:

Si bien en las figuras sus pares de ángulos homólogos tienen la misma medida, porque todos son ángulos rectos (miden 90º), las figuras no son semejantes, porque sus pares de lados no son proporcionales.

En cambio, estos dos cuadriláteros tienen lados homólogos con igual medida, pero los ángulos homólogos no miden igual. Por lo tanto, las figuras claramente no son semejantes.

Razón de semejanza

Si dos figuras son semejantes, el cociente entre los lados homólogos es el mismo y recibe el nombre de razón de semejanza.

Denotando los lados de una de las figuras como a, b, c, d… y los correspondientes de la otra figura como a’, b’, c’, d’…, las figuras son semajantes si:

Perímetros y áreas de figuras semejantes

La razón de semejanza permite obtener relaciones entre los perímetros, las áreas y los volúmenes de dos figuras semejantes.

Razón de perímetros de dos figuras semejantes

El perímetro P de un polígono se define como la suma de todos sus lados. Si se tiene una figura cuyos lados son a’, b’, c’, d’…, su perímetro P’ es:

P’ = a’ + b’ + c’ + d’ ….

Si otro polígono es semejante a este, y sus lados son a, b, c, d…, se cumple que:

Y, por lo tanto:

a = r∙a’

Se puede afirmar otro tanto para los demás lados de esta figura. Así que el perímetro P se expresa como:

P = a + b + c + d …. = r∙a’ + r∙b’ + r∙c’ + r∙d’ + …

Puesto que “r” es un factor común a todos los sumandos, la relación entre P y P’ es:

P = r∙P’

Esto significa que la razón de los perímetros entre dos polígonos semejantes, es igual a la razón de semejanza.

Razón de áreas de dos figuras semejantes

Si dos figuras semejantes tienen respectivamente áreas A y A’, estas se relacionan mediante:

A = r²∙A’

Donde “r” es la razón de semejanza de las figuras.

Razón de volúmenes de dos figuras semejantes

Sean dos figuras tridimensionales semejantes, cuyos volúmenes son, respectivamente, V y V’. La relación entre ellos, a través de “r” es:

V = r³∙V’

Ejemplos

Planos

Se pueden representar porciones de un terreno, la planta de una edificación o incluso una prenda de ropa, a una escala más pequeña sobre una hoja de papel. Los planos tienen la ventaja de poder llevarse consigo y hacer las modificaciones pertinentes con facilidad, antes de ponerlas en práctica sobre el objeto real.

Mapas

Por lo general son representaciones en el plano de una gran extensión de terreno, desde una aldea hasta los continentes. También se hacen a una escala determinada.

Tienen numerosas aplicaciones y los hay de muchos tipos. Por ejemplo, mediante un mapa se puede describir el terreno, y al ubicarse sobre un punto específico, se determina la mejor ruta para ir desde ese punto hasta otro.

Maquetas

Son representaciones tridimensionales a escala de objetos como automóviles, edificios y construcciones en general.

Ejercicio resuelto

Los valores que siguen corresponden a los lados de una pareja de triángulos semejantes. Hallar la razón de semejanza y los valores de “x” y “y”:

Triángulo 1: 5, 8, 10

Triángulo 2: 150, x, y

Solución

La razón de semejanza es el cociente:

r = 150/5 = 30

Por lo tanto:

x = 30 × 8 = 240

y = 10 × 30 = 300