Método de Gauss-Seidel: explicación, aplicaciones, ejemplos
El método de Gauss-Seidel es un procedimiento iterativo para hallar soluciones aproximadas a un sistema de ecuaciones algebraicas lineales con una precisión arbitrariamente elegida. El método se aplica a matrices cuadradas con elementos no nulos en sus diagonales y la convergencia se garantiza si la matriz es diagonalmente dominante.
Fue creado por Carl Friedrich Gauss (1777-1855), el cual le hizo una demostración privada a uno de sus estudiantes en 1823. Posteriormente fue publicado formalmente por Philipp Ludwig von Seidel (1821-1896) en 1874, de ahí que lleve el nombre de ambos matemáticos.

Para una comprensión cabal del método, es preciso saber que una matriz es diagonalmente dominante cuando el valor absoluto del elemento diagonal de cada fila es mayor o igual que la suma de los valores absolutos de los otros elementos de esa misma fila.
Matemáticamente se expresa así:
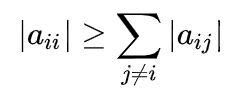
Índice del artículo
- 1 Explicación mediante un caso sencillo
- 2 Aplicaciones
- 3 Ejemplos del método de Gauss-Seidel
- 4 Referencias
Para ilustrar en qué consiste el método de Gauss-Seidel tomaremos un caso sencillo, en el cual se puede encontrar los valores de X y Y en el sistema de ecuaciones lineales 2×2 que se muestra a continuación:
5X + 2Y = 1
X – 4Y = 0
1- En primer lugar hay que determinar si la convergencia es segura. De inmediato se observa que, en efecto, se trata de un sistema diagonalmente dominante, ya que en la primera fila el primer coeficiente tiene mayor valor absoluto que los demás de la primera fila:
|5|>|2|
Igualmente, el segundo coeficiente de la segunda fila también es diagonalmente dominante:
|-4|>|1|
2- Se despejan la variables X e Y:
X = (1 – 2Y)/5
Y = X/4
3- Se coloca un valor inicial arbitrario, denominado “semilla”: Xo=1, Yo=2.
4-Comienza la iteración: para obtener la primera aproximación X1, Y1 se sustituye la semilla en la primera ecuación del paso 2 y el resultado en la segunda ecuación del paso 2:
X1 = (1 – 2 Yo)/5 = (1 – 2×2)/5 = -3/5
Y1 = X1 / 4 = (-3/5) / 4 = -3/20
5- Se procede en forma similar para obtener la segunda aproximación de la solución del sistema de ecuaciones:
X2 = (1 – 2 Y1)/5 = (1 – 2x(-3/20))/5 = 13/50
Y2 = X2/4 = (13/50)/4 = 13/200
6- Tercera iteración:
X3 = (1 – 2 Y2)/5 = (1 – 2 (13/200))/5 = 87/500
Y3 = X3 / 4 = (87/500)/4 = 87/2000
7- Cuarta iteración, como iteración final de este caso ilustrativo:
X4 = (1 – 2 Y3)/5 = (1 – 2 (87/2000))/5 = 913/5000
Y4 = X4 / 4 = (913/5000)/4 = 913/20000
Estos valores coinciden bastante bien con la solución hallada mediante otros métodos de resolución. El lector puede comprobarlo rápidamente con ayuda de algún programa matemático online.
Como puede observarse, en el método de Gauss-Seidel hay que sustituir en la siguiente variable, los valores aproximados obtenidos para la variable previa en ese mismo paso. Esto lo diferencia de otros métodos iterativos como el de Jacobi, en el cual cada paso requiere las aproximaciones de la etapa previa.
El método de Gauss-Seidel no es un procedimiento paralelo, mientras que el de Gauss-Jordan si lo es. También es la razón de que el método de Gauss-Seidel tenga una convergencia más rápida -en menos pasos- que el método de Jordan.
En cuanto a la condición de matriz diagonalmente dominante, esta no siempre se satisface. Sin embargo, en la mayoría de los casos basta con intercambiar las filas del sistema original para que se cumpla la condición. Además, el método converge casi siempre, aun cuando no se cumpla la condición de dominancia diagonal.
El resultado previo, obtenido mediante cuatro iteraciones del método de Gauss-Seidel, puede escribirse en forma decimal:
X4= 0,1826
Y4= 0,04565
La solución exacta al sistema de ecuaciones planteado es:
X= 2/11 = 0,1818
Y= 1/22= 0,04545.
Así que apenas con 4 iteraciones se obtiene un resultado con una milésima de precisión (0,001).
En la figura 1 se ilustra cómo las sucesivas iteraciones convergen rápidamente a la solución exacta.
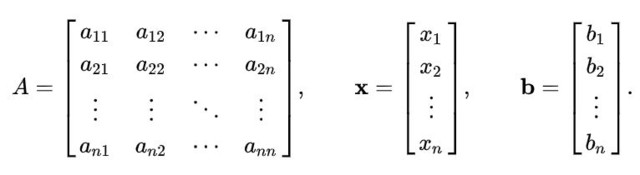
El método de Gauss-Seidel no se limita únicamente a sistema de ecuaciones lineales 2×2. Puede generalizarse el procedimiento anterior para resolver un sistema lineal de n ecuaciones con n incógnitas, el cual se representa matricialmente así:
AX = b
Donde A es una matriz n x n, mientras X es el vector n componentes de las n variables a ser calculadas; y b es un vector que contiene los valores de los términos independientes.
Para generalizar la secuencia de iteraciones aplicadas en el caso ilustrativo a un sistema n x n, del que quiere calcularse la variable Xi, se aplicará la siguiente fórmula:
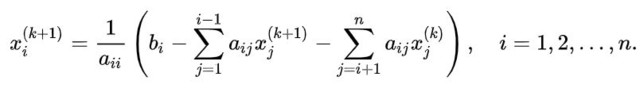
En esta ecuación:
– k es el índice para el valor obtenido en la iteración k.
-k+1 indica el nuevo valor en la siguiente.
El número final de iteraciones queda determinado cuando el valor obtenido en la iteración k+1 difiere del obtenido inmediatamente antes, en una cantidad ε que es justamente la precisión deseada.
Escribir un algoritmo general que permita calcular el vector de soluciones aproximadas X de un sistema lineal de ecuaciones nxn, dadas la matriz de coeficientes A, el vector de términos independientes b, el número de iteraciones (iter) y el valor inicial o “semilla” del vector X.
Solución
El algoritmo consta de dos ciclos “Para”, uno para el número de iteraciones y el otro para el número de variables. Quedaría de la siguiente forma:
Para k ∊ [1..iter]
Para i ∊ [1..n]
X[i] :=( 1/A[i,i] )*( b[i] – ∑j=1n(A[i,j]*X[j]) + A[i,i]*X[i] )
Comprobar el funcionamiento del algoritmo anterior mediante su aplicación en el software matemático SMath Studio de uso libre y gratuito, disponible para Windows y Android. Tomar como ejemplo el caso de la matriz 2×2 que nos sirvió para ilustrar el método de Gauss-Seidel.
Solución
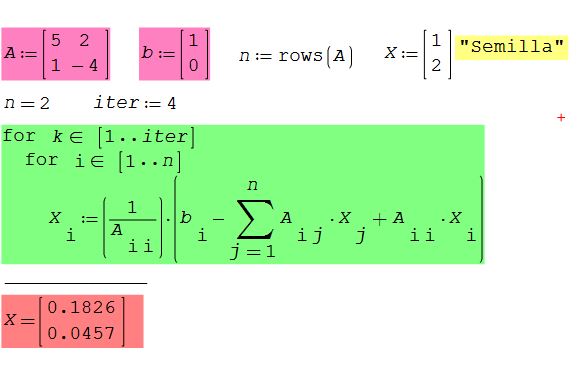
Aplicar el algoritmo de Gauss-Seidel para el siguiente sistema de ecuaciones 3×3, el cual se ha ordenado previamente de modo tal, que los coeficientes de la diagonal son dominantes (es decir de mayor valor absoluto que los valores absolutos de los coeficientes de la misma fila):
9 X1 + 2 X2 – X3 = -2
7 X1 + 8 X2 + 5 X3 = 3
3 X1 + 4 X2 – 10 X3 = 6
Usar como semilla el vector nulo y considerar cinco iteraciones. Comentar el resultado.
Solución

Para el mismo sistema con 10 iteraciones en vez de 5 se obtienen los siguientes resultados: X1=-0.485; X2=1.0123; X3=-0.3406
Esto nos indica que basta con cinco iteraciones para obtener tres decimales de precisión y que el método converja rápidamente a la solución.
Mediante el algoritmo de Gauss-Seidel dado anteriormente, hallar la solución del sistema de ecuaciones 4×4 que se da a continuación:
10 x1 – x2 + 2 x3 + 0 x4 = 6
-1 x1 + 11 x2 – 1 x3 + 3 x4 = 25
2 x1 – 1 x2 + 10 x3 – 1 x4 = -11
0 x1 + 3 x2 – 1 x3 + 8 x4 = 15
Para arrancar el método, haga uso de esta semilla:
x1=0, x2=0, x3=0 y x4=0
Considere 10 iteraciones y estime el error del resultado, comparando con la iteración número 11.
Solución

Al comparar con la siguiente iteración (la número 11), el resultado es idéntico. Las mayores diferencias entre las dos iteraciones son del orden de 2×10-8, lo que significa que la solución mostrada tiene una precisión de por lo menos siete decimales.
- Métodos iterativos de solución. Gauss-Seidel. Recuperado de: cimat.mx
- Métodos numéricos. Gauss-Seidel. Recuperado de: test.cua.uam.mx
- Numérico: Método de Gauss-Seidel. Recuperado de: aprendeenlinea.udea.edu.co
- Wikipedia. Gauss-Seidel method. Recuperado de: en. wikipedia.com
- Wikipedia. Método de Gauss-Seidel. Recuperado de: es.wikipedia.com
