Ley de Biot-Savart: fórmula, demostración, aplicaciones, ejercicios
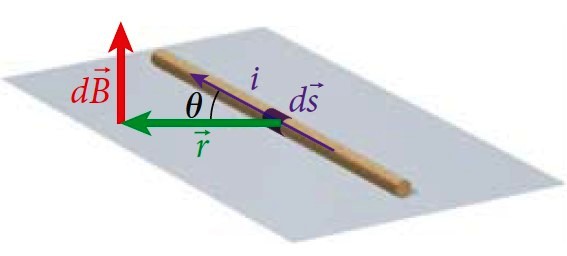
La ley de Biot-Savart establece una relación entre el campo magnético dB en un punto P, producido por un alambre delgado que transporta una corriente I y cuya longitud diferencial es ds. Dicha ley se utiliza para encontrar el campo magnético de distribuciones de corriente mediante el principio de superposición.
Esto significa que para calcular el campo magnético total en el punto P, debemos sumar todas las contribuciones que cada parte diferencial ds del alambre aporta. Y esta suma se hace a través de una integral llevada a cabo sobre toda la distribución de corriente.
De esta manera se puede calcular el campo que producen alambres con corriente de distintas geometrías.
La ley de Biot – Savart lleva el nombre de los dos físicos franceses que la descubrieron en 1820: Jean Marie Biot (1774-1862) y Felix Savart (1791-1841). Para lograrlo, debieron estudiar la intensidad y la forma del campo magnético producido por numerosas distribuciones de corriente.
Índice del artículo
- 1 Fórmula
- 2 Demostración de la ley de Biot-Savart
- 3 Aplicaciones de la ley de Biot-Savart
- 4 Ejercicio resuelto
- 5 Referencias
La expresión matemática de la ley de Biot-Savart es la siguiente:
Mantiene analogías con su equivalente para calcular el campo eléctrico: la ley de Coulomb, solamente que el campo magnético dB en P es perpendicular al plano donde se encuentra el alambre. Esto lo podemos ver en la figura 1.
La expresión anterior también se puede escribir de la siguiente manera:
En ambas expresiones, r es el vector de posición, dirigido desde el elemento de corriente Ids hasta el punto donde se desea calcular el campo.
Por su parte, r con acento circunflejo es el vector unitario que va dirigido en su misma dirección y sentido, pero con módulo igual a 1. El vector r se representa así:
Además de los mencionados vectores, la fórmula contiene la constante μo, llamada permeabilidad del vacío y cuyo valor es:
μo = 4π x10-7 T.m/ A.
Si queremos calcular el vector campo magnético es preciso integrar sobre toda la distribución de corriente, para lo cual necesitamos los datos acerca de su geometría:
La ley de Biot-Savart involucra un producto vectorial entre los vectores Ids y r. El resultado de un producto vectorial entre dos vectores también es un vector.
En este caso el módulo del producto vectorial Ids x r es: (Ids)⋅r⋅senθ, donde θ es el ángulo entre Ids y r, tal como se muestra en la figura 1.
De esta manera la magnitud del campo dB viene dada por:
La dirección y el sentido se pueden determinar con la regla de la mano derecha, que se ilustra en esta figura:
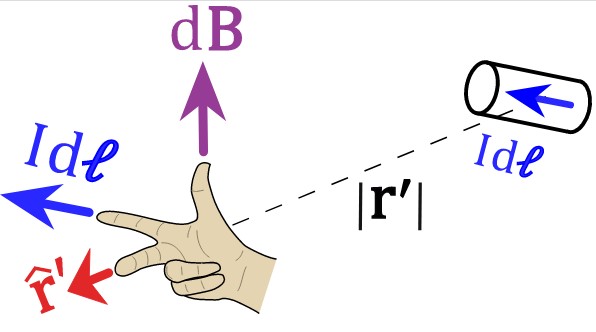
Invitamos al lector para que posicione su mano derecha siguiendo los vectores de las figuras 1 y 2. Para la figura 1, el dedo índice debe apuntar a la izquierda, siguiendo a Ids o Idl, el dedo medio apunta según el vector r unitario.
Y por último el pulgar está dirigido hacia arriba y esta es la dirección del campo magnético.
La ley de Biot-Savart es de carácter eminentemente experimental, lo que quiere decir que su formulación proviene de muchas observaciones acerca del comportamiento del campo magnético producido por alambres de corriente.
Estas fueron las observaciones de los científicos franceses acerca del campo magnético dB:
-La magnitud de dB es inversamente proporcional a r2.
–También es directamente proporcional a la magnitud del elemento de corriente, al que se llama Ids y también al sen θ, donde θ es el ángulo entre los vectores ds y r.
-dB es perpendicular tanto a Ids –la dirección de la corriente- como a r.
-La dirección de dB es tangencial a una circunferencia de radio r centrada en el alambre. En otras palabras, el campo B producido por un segmento de corriente consiste en circunferencias concéntricas al alambra.
-El sentido en que gira B viene dado por la regla del pulgar derecho: se apunta el pulgar derecho en la dirección de la corriente y los cuatro dedos restantes se enroscan alrededor del alambre, siguiendo la circulación del campo.
Todas estas observaciones se combinan en la expresión matemática de la ley descrita previamente.
Cuando la distribución de corriente tiene alta simetría, la integral se puede resolver fácilmente, veamos algunos casos:
Un alambre rectilíneo de longitud L transporta una corriente I, como el que aparece en la figura.
La misma ilustra la geometría necesaria para el cálculo del campo. Este resulta perpendicular a la hoja de papel, saliente al plano si la corriente fluye de izquierda a derecha, y entrante en caso contrario (comprobarlo con la regla de la mano derecha).
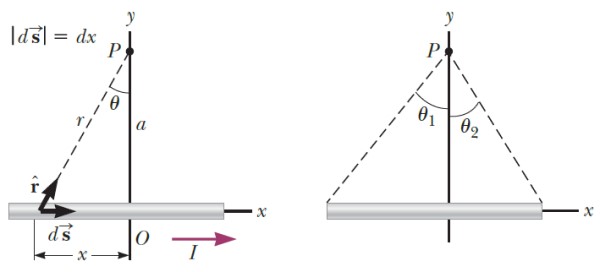
Sea k el vector unitario en la dirección perpendicular al plano, luego de llevar a cabo el proceso de integrar, el campo magnético que el alambre produce en P es:
La espira circular de radio a transporta una corriente como se muestra en la figura y produce un campo magnético dB -en verde oscuro- en el punto P sobre el eje axial, a una distancia x del centro.
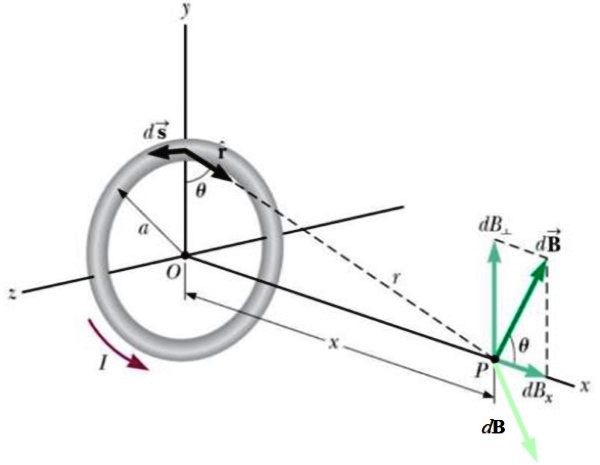
Otro elemento de corriente situado en el lado opuesto, produciría otra contribución al campo dB (verde claro), tal que su componente vertical se cancela con la primera.
El resultado es que el campo magnético neto es horizontal, por lo que únicamente se integra sobre estas componentes, dando como resultado:
Se tiene un alambre sumamente largo que transporta una corriente de 2 A fluyendo como se muestra en la imagen. Calcular la magnitud del campo magnético a una distancia radial de 5 cm del alambre.
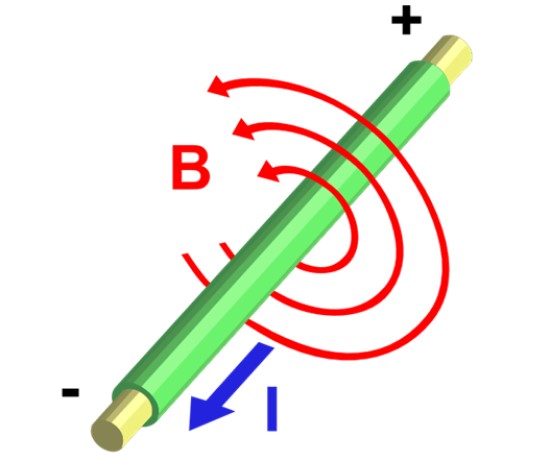
Ya que se trata de un alambre muy largo, podemos tomar la expresión para el segmento rectilíneo y hacer θ1=0º y θ2 = 180º para los ángulos límite. Esto es suficiente para que la longitud del alambre tienda a infinito.
De esta manera tendremos el campo es:
Ahora sustituimos los valores del enunciado:
I = 2 A
r = 5 x10-2 m
μo= 4π x10-7 T.m/ A
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Figueroa, D. 2005. Serie: Física para Ciencias e Ingeniería. Volumen 6. Electromagnetismo. Editado por Douglas Figueroa (USB).
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Resnick, R. 1999. Física. Vol. 1. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volumen 1.
- Serway, R., Jewett, J. 2008. Física para Ciencias e Ingeniería. Volumen 2. 7ma. Ed. Cengage Learning.
