Función sobreyectiva: definición, propiedades, ejemplos
Una función sobreyectiva es toda relación donde cada elemento perteneciente al codominio es imagen de al menos un elemento del dominio. También conocidas como función sobre, son parte de la clasificación de funciones con respecto a la forma en que se relacionan sus elementos.
Por ejemplo una función F : A → B definida por F ( x ) = 2x
Lo cual se lee “F que va de A hasta B definida por F ( x ) = 2x”
Toca definir los conjuntos de partida y llegada A y B.
A : { 1 , 2 , 3 , 4 , 5 } Ahora los valores o imágenes que arrojarán cada uno de estos elementos al ser evaluados en F, serán los elementos del codominio.
F ( 1 ) = 2
F ( 2 ) = 4
F ( 3 ) = 6
F ( 4 ) = 8
F ( 5 ) = 10
Formando así el conjunto B : { 2 , 4 , 6 , 8 , 10 }
Se puede concluir entonces que:
F : { 1 , 2 , 3 , 4 , 5 } → { 2 , 4 , 6 , 8 , 10 } definida por F ( x ) = 2x Es una función sobreyectiva
Cada elemento del codominio, debe resultar de al menos una operación de la variable independiente a través de la función en cuestión. No existe limitante de imágenes, un elemento del codominio puede ser imagen de más de un elemento del dominio y seguirse tratando de una función sobreyectiva.
En la imagen se muestran 2 ejemplos con funciones sobreyectivas.
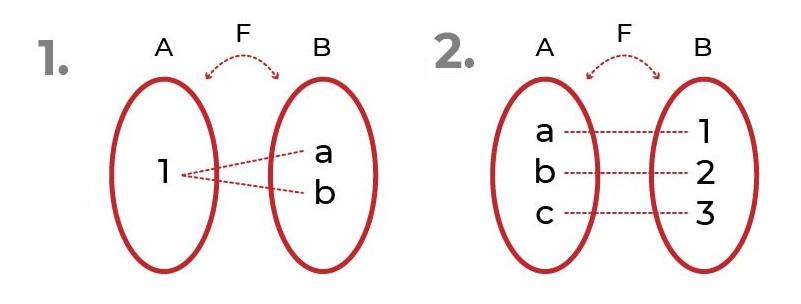
En la primera se observa que las imágenes pueden ser referidas de un mismo elemento, sin esto comprometer la sobreyectividad de la función.
En la segunda vemos una distribución equitativa entre dominio e imágenes. Esto da pie a la función biyectiva, donde se deben cumplir los criterios de función inyectiva y función sobreyectiva.
Otro método para identificar a las funciones sobreyectivas, es verificar si el codominio es igual al rango de la función. Esto quiere decir que si el conjunto de llegada es igual a las imágenes que proporciona la función al evaluar la variable independiente, la función es sobreyectiva.
Índice del artículo
Para considerar sobreyectiva a una función se debe cumplir lo siguiente:
Sea F : Df → Cf
∀ b ℮ Cf E a ℮ Df / F ( a ) = b
Esta es la manera algebraica para establecer que para todo “b” que pertenece a Cf existe un “a” que pertenece a Df tal que, la función F evaluada en “a” es igual a “b”.
La sobreyectividad es una particularidad de las funciones, donde el codominio y el rango son semejantes. Así, los elementos evaluados en la función componen el conjunto de llegada.
En ocasiones una función que no es sobreyectiva, puede someterse a ciertos condicionamientos. Estás nuevas condiciones pueden convertirla en una función sobreyectiva.
Son válidos todo tipo de modificaciones al dominio y codominio de la función, donde el objetico es cumplir las propiedades de sobreyectividad en la relación correspondiente.
Para cumplir las condiciones de sobreyectividad se deben aplicar distintas técnicas de condicionamiento, esto con la finalidad de lograr que cada elemento del codominio esté dentro del conjunto de imágenes de la función.
- Sea la función F : R → R definida por la recta F ( x ) = 8 – x
R : [ Todos los números reales ]
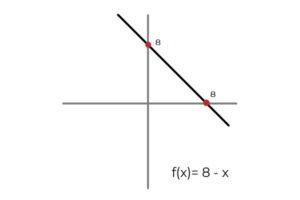
En este caso la función describe una recta continua, la cual abarca todos los números reales tanto en su dominio como rango. Debido a que el rango de la función Rf es igual al codominio R se puede concluir que:
F : R → R definida por la recta F ( x ) = 8 – x es una función sobreyectiva.
Esto aplica para todas las funciones lineales (Funciones cuyo mayor grado de la variable es uno).
- Estudiar la función F : R → R definida por F ( x ) = x2 : Definir si es una función sobreyectiva. En caso de no serlo, muestre los condicionamientos necesarios para hacerla sobreyectiva.
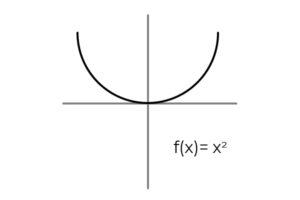
Lo primero a tener en cuenta es el codominio de F, el cual se compone de los números reales R. No existe forma de que la función arroje valor negativos, lo que excluye a los reales negativos de entre las posibles imágenes.
Condicionando el codominio al intervalo [ 0 , ∞ ]. Se evita dejar elementos del codominio sin relacionar a través de F.
Las imágenes se repiten para pares de elementos de la variable independiente, como por ejemplo x = 1 y x = – 1. Pero esto solo afecta a la inyectividad de la función, no siendo un problema para este estudio.
De esta forma se puede concluir que:
F : R →[ 0 , ∞ ) definida por F ( x ) = x2 Es una función sobreyectiva
- Definir las condiciones del codominio que harían sobreyectivas a las funciones
F : R → R definida por F ( x ) = Sen ( x )
F : R → R definida por F ( x ) = Cos ( x )
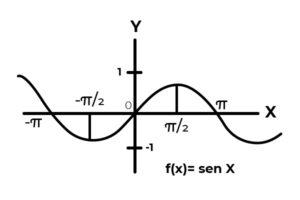
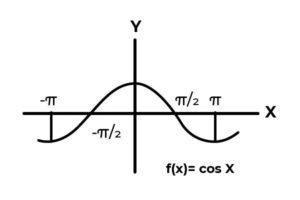
El comportamiento de las funciones trigonométricas es similar al de ondas, siendo muy común encontrar repeticiones de la variable dependiente entre las imágenes. También en la mayoría de los casos el rango de la función se ve limitado a uno o varios sectores de la recta real.
Este es el caso de las funciones Seno y Coseno. Donde sus valores fluctúan en el intervalo [ -1 , 1 ]. Dicho intervalo debe condicionar el codominio para lograr la sobreyectividad de la función.
F : R →[ -1 , 1 ] definida por F ( x ) = Sen ( x ) Es una función sobreyectiva
F : R →[ -1 , 1 ] definida por F ( x ) = Cos ( x ) Es una función sobreyectiva
- Estudiar la función
F : [ 0 , ∞ ) → R definida por F ( x ) = ± √x denote si se trata de una función sobreyectiva
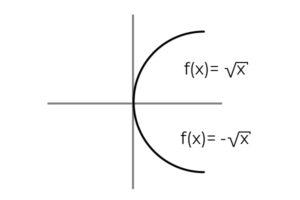
La función F ( x ) = ± √x posee la particularidad que define 2 variables dependientes a cada valor de “ x “ . Es decir, el rango recibe 2 elementos por cada uno que se efectúa en el dominio. Se debe verificar un valor positivo y negativo para cada valor de “ x “.
Al observar el conjunto de partida se nota que el dominio ya ha sido restringido, esto en pro de evitar las indeterminaciones producidas al evaluar un número negativo dentro de una raíz par.
Al verificar el rango de la función se nota que cada valor del codominio pertenece al rango.
De esta manera se puede concluir que:
F : [ 0 , ∞ ) → R definida por F ( x ) = ± √x Es una función sobreyectiva
- Estudiar la función F ( x ) = Ln x denote si se trata de una función sobreyectiva. Condicione los conjuntos de llegada y partida para adaptar la función a los criterios de sobreyectividad.
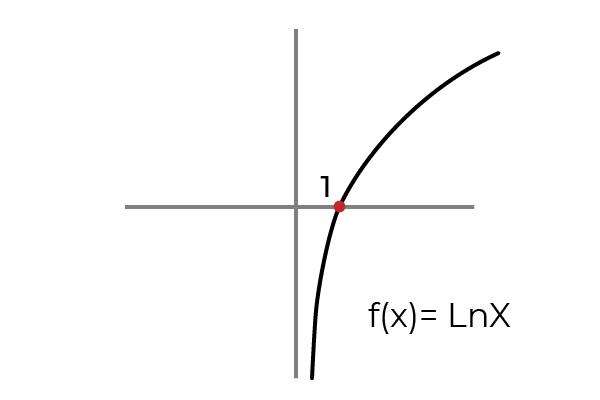
Tal como se muestra en la gráfica la función F ( x ) = Ln x está definida para los valores de “ x “ mayores que cero. Mientras los valores de “ y “ o las imágenes pueden tomar cualquier valor real.
De esta forma podemos restringir el dominio de F ( x ) = al intervalo ( 0 , ∞ )
Mientras el rango de la función se puede mantener como el conjunto de los números reales R.
Considerando esto se puede concluir que:
F : [ 0 , ∞ ) → R definida por F ( x ) = Ln x Es una función sobreyectiva
- Estudiar la función valor absoluto F ( x ) = | x | y designar los conjuntos de llegada y partida que se ajunten a los criterios de sobreyectividad.
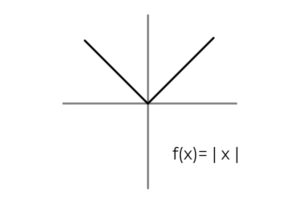
El dominio de la función se cumple para todos los números reales R. De esta forma el único condicionamiento se debe realizar en el codominio, tomando en cuenta que la función valor absoluto solo toma valores positivos.
Se procede a establecer el codominio de la función igualándolo al rango de la misma
[ 0 , ∞ )
Ahora se puede concluir que:
F : [ 0 , ∞ ) → R definida por F ( x ) = | x | Es una función sobreyectiva
- Verificar si las siguientes funciones son sobreyectivas:
- F : ( 0 , ∞ ) → R definida por F ( x ) = Log ( x + 1 )
- F : R → R definida por F ( x ) = x3
- F : R →[ 1 , ∞ ) definida por F ( x ) = x2 + 1
- [ 0 , ∞ ) → R definida por F ( x ) = Log (2x + 3)
- F : R → R definida por F ( x ) = Sec x
- F : R – { 0 } → R definida por F ( x ) = 1 / x
- Introduction to Logic and Critical Thinking. Merrilee H. Salmon. University of Pittsburgh
- Problems in Mathematical Analysis. Piotr Biler, Alfred Witkowski. University of Wroclaw. Poland.
- Elements of Abstract Analysis. Mícheál O’Searcoid PhD. Department of mathematics. University college Dublin, Beldfield, Dublind 4
- Introduction to Logic and to the Methodology of the Deductive Sciences. Alfred Tarski, New York Oxford. Oxford University press.
- Principios de análisis matemático. Enrique Linés Escardó. Editorial Reverté S. A 1991. Barcelona España.
