Heptadecágono: propiedades, diagonales, perímetro, área
El heptadecágono es un polígono regular de 17 lados y 17 vértices. Su construcción puede hacerse al estilo euclidiano, es decir usando solo la regla y el compás. Fue el gran genio de las matemáticas Carl Friedrich Gauss (1777-1855), contando apenas 18 años de edad, quien encontró el procedimiento para su construcción en 1796.
Al parecer, Gauss se sintió siempre muy inclinado por esta figura geométrica, a tal punto que desde el día que descubrió su construcción decidió ser matemático. También se cuenta que quiso que el heptadecágono fuera grabado en su lápida.

Gauss también encontró la fórmula para determinar cuáles polígonos regulares tienen la posibilidad de construirse con regla y compás, ya que algunos no tienen construcción euclidiana exacta.
Índice del artículo
En cuanto a sus características, como todo polígono, es importante la suma de sus ángulos internos. En un polígono regular de n lados, la suma viene dada por:
Sa(n) = (n -2) *180º.
Para el heptadecágono el número de lados n es 17, lo cual significa que la suma de sus ángulos internos es:
Sa(17) = (17 – 2) * 180º = 15 * 180º = 2700º.
Esta suma, expresada en radianes queda así:
Sa(17) = (17 – 2) * π = 15 * π = 15π
De las fórmulas anteriores se puede deducir fácilmente que cada ángulo interno de un heptadecágono tiene una medida α exacta dada por:
α = 2700º/17 = (15/17)π radianes
Se sigue que el ángulo interno en forma aproximada es:
α ≈ 158,824º
Las diagonales y el perímetro son otros aspectos importantes. En cualquier polígono el número de diagonales es:
D = n ( n – 3 ) / 2 y en el caso del heptadecágono, como n = 17, se tiene entonces que D = 119 diagonales.
Por otro lado, si la longitud de cada lado del heptadecágono es conocida, entonces el perímetro del heptadecágono regular se encuentra simplemente sumando 17 veces esa longitud, o lo que es equivalente 17 veces la longitud d de cada lado:
P = 17 d
En ocasiones solo se conoce el radio r del heptadecágono, por lo que es necesario desarrollar una fórmula para este caso.
Con este fin se introduce el concepto de apotema. El apotema es el segmento que va desde el centro del polígono regular hasta el punto medio de un lado. El apotema relativo a un lado es perpendicular a ese lado (ver figura 2).
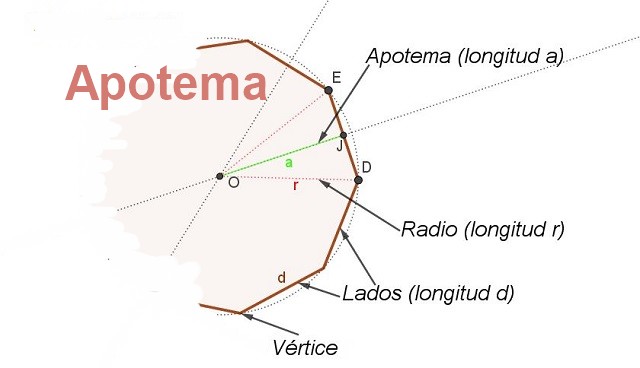
Además el apotema es bisectriz del ángulo con vértice central y lados sobre dos vértices consecutivos del polígono, esto permite encontrar una relación entre el radio r y el lado d.
Si se denomina β al ángulo central DOE y tomando en cuenta que el apotema OJ es bisectriz se tiene EJ = d/2 = r Sen(β/2), de donde se tiene una relación para encontrar la longitud d del lado de un polígono conocido su radio r y su ángulo central β:
d = 2 r Sen(β/2)
En el caso del heptadecágono β =360º/17 por lo que se tiene:
d = 2 r Sen(180º/17) ≈ 0,3675 r
Finalmente se obtiene la fórmula del perímetro del heptadecágono conocido su radio:
P = 34 r Sen(180º/17) ≈ 6.2475 r
El perímetro de un heptadecágono se acerca al perímetro de la circunferencia que lo circunscribe, pero su valor es menor, vale decir que el perímetro de la circunferencia circunscrita es Pcir = 2π r ≈ 6.2832 r.
Para determinar el área del heptadecágono nos referiremos a la figura 2, en la que se muestran los lados y el apotema de un polígono regular de n lados. En dicha figura el triángulo EOD tiene un área igual a la base d (lado de polígono) por la altura a (apotema del polígono) divida entre 2:
Área EOD = ( d x a ) / 2
De modo que conocido el apotema a del heptadecágono y el lado d del mismo su área es:
Área heptadecágono = (17/2) (d x a)
Para conseguir una fórmula para el área del heptadecágono conociendo la longitud de sus diecisiete lados, es necesario conseguir una relación entre la longitud del apotema a y el lado d.
En referencia a la figura 2 se tiene la siguiente relación trigonométrica:
Tan(β/2) = EJ / OJ = (d/2)/ a, siendo β al ángulo central DOE. De modo que el apotema a puede calcularse si se conoce la longitud d del lado del polígono y el ángulo central β:
a = (d/2) Cotan(β/2)
Si ahora se sustituye esta expresión para el apotema, en la fórmula del área del heptadecágono obtenida en la sección previa, se tiene:
Área heptadecágono = (17/4) (d2) Cotan(β/2)
Siendo β =360º/17 para el heptadecágono, por lo que se tiene finalmente la fórmula deseada:
Área heptadecágono = (17/4) (d2) Cotan(180º/17)
En las secciones previas se había encontrado una relación entre el lado d de un polígono regular y su radio r, siendo dicha relación la siguiente:
d = 2 r Sen(β/2)
Esta expresión para d se introduce en la expresión obtenida en el apartado anterior para el área. Si se hacen las sustituciones y simplificaciones pertinentes, se obtiene la fórmula que permite calcular el área del heptadecágono:
Área heptadecágono = (17/2) (r2) Sen(β) = (17/2) (r2) Sen(360º/17)
Una expresión aproximada para el área es:
Área heptadecágono = 3,0706 (r2)
Como era de esperarse, esta área es un poco menor que el área del círculo que circunscribe al heptadecágono Acirc = π r2 ≈ 3,1416 r2. Para ser precisos, es 2% menor que la de su círculo circunscrito.
Para que un heptadecágono tenga lados de 2 cm, ¿qué valor debe tener el radio y el diámetro de la circunferencia circunscrita? Hallar también el valor del perímetro.
Para responder la pregunta es necesario recordar la relación que hay entre el lado y el radio de un polígono regular de n lados:
d = 2 r Sen(180º / n)
Para el heptadecágono n = 17, por lo que d = 0,3675 r, es decir que el radio del heptadecágono es r = 2 cm / 0,3675 = 5,4423 cm o
10,8844 cm de diámetro.
El perímetro de un heptadecágono de 2 cm de lado es P = 17* 2 cm = 34 cm.
¿Cuánto vale el área de un heptadecágono regular de 2 cm de lado?
Hay que remitirse a la fórmula demostrada en la sección precedente, que permite hallar el área de un heptadecágono cuando se tiene la longitud d de su lado:
Área heptadecágono = (17/4) (d2) / Tan(180º/17)
Al sustituir d= 2 cm en la fórmula anterior se obtiene:
Área = 90,94 cm
- C. E. A. (2003). Elementos de geometría: con ejercicios y geometría del compás. Universidad De Medellín.
- Campos, F., Cerecedo, F. J. (2014). Matemáticas 2. Grupo Editorial Patria.
- Freed, K. (2007). Discover Polygons. Benchmark Education Company.
- Hendrik, V. (2013). Generalized Polygons. Birkhäuser.
- IGER. (s.f.). Matemática Primer Semestre Tacaná. IGER.
- Jr. geometry. (2014). Polygons. Lulu Press, Inc.
- Miller, Heeren, & Hornsby. (2006). Matemática: Razonamiento Y Aplicaciones (Décima Edición). Pearson Educación.
- Patiño, M. (2006). Matemáticas 5. Editorial Progreso.
- Sada, M. Polígono regular de 17 lados con regla y compás. Recuperado de: geogebra.org
- Wikipedia. Heptadecágono. Recuperado de: es.wikipedia.com
