Decágono: regular, irregular, propiedades, ejemplos
El decágono es una figura plana con forma de polígono de 10 lados y 10 vértices o puntas. Los decágonos pueden ser regulares o irregulares, en el primer caso todos los lados y ángulos internos tienen la misma medida, mientras que en el segundo los lados y/o los ángulos son diferentes entre sí.
En la figura 1 se muestran ejemplos de decágonos de cada tipo y como podemos ver, el decágono regular es muy simétrico.
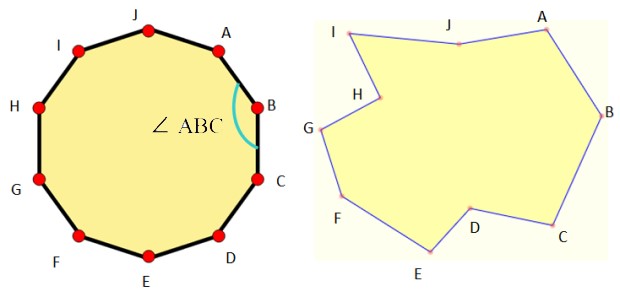
Los elementos básicos de todo decágono son:
-Lados, los segmentos de recta que al unirse forman el decágono.
-Vértices, o puntos entre cada lado consecutivo.
-Ángulos internos y externos entre lados adyacentes.
-Diagonales, segmentos que unen dos vértices no consecutivos.
Los vértices se denominan mediante letras mayúsculas, tal como se muestra en la figura 1, donde se utilizaron las primeras letras del alfabeto, pero se puede utilizar cualquier letra.
Los lados se simbolizan con las dos letras de los vértices entre los que se encuentran, por ejemplo el lado AB es el que está entre los vértices A y B. De igual modo se hace con las diagonales, así tenemos la diagonal AF, que une los puntos A y F.
Para los ángulos usamos este símbolo: ∠, semejante a una L inclinada. Por ejemplo el ángulo ∠ ABC es aquel cuyo vértice es B y cuyos lados son los segmentos AB y BC.
Índice del artículo
En el decágono regular, todos los lados tienen la misma medida, así como los ángulos internos. Por lo tanto se dice que es equilátero (lados iguales) y equiángulo (ángulos iguales). Es una figura muy simétrica
Para encontrar la medida de los ángulos internos de un polígono regular, incluido el decágono regular, se emplea la siguiente fórmula:
Donde:
-I es la medida del ángulo en grados.
-n es el número de lados del polígono. En el caso del decágono n= 10.
Sustituyendo n= 10 en la fórmula anterior obtenemos lo siguiente:
Ahora bien, se dice que un polígono es convexo si sus medidas angulares son menores de 180º, en caso contrario el polígono es cóncavo. Como cualquier ángulo interno del decágono regular mide 144º y es menor de 180º, entonces se trata de un polígono convexo.
La suma de las medidas de los ángulos internos de cualquier polígono es, en grados:
S = (n-2) x 180º; n siempre es mayor que 2
En esta fórmula tenemos que:
-S es la suma de las medidas de los ángulos internos.
-n es el número de lados. Para el decágono n = 10
Aplicando la fórmula para n= 10 resulta:
S = (10 – 2) x 180º = 1440º
Un ángulo exterior se forma entre un lado y la extensión del lado adyacente, veamos:
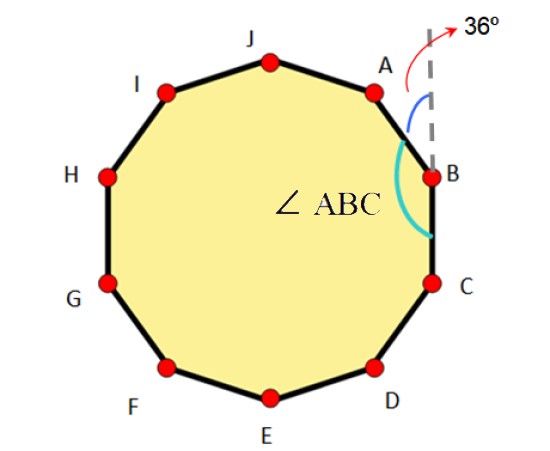
El ángulo ∠ ABC más el ángulo externo suman 180º, es decir, son suplementarios. Por lo tanto el ángulo externo es igual a 180º-144º = 36º, como vemos en la figura.
Como se dijo antes, las diagonales son los segmentos que unen vértices no consecutivos. ¿Cuántas diagonales podemos trazar en un decágono? Cuando el número de vértices es pequeño se pueden contar fácilmente, pero cuando ese número aumenta se puede perder la cuenta.
Por fortuna hay una fórmula para conocer el número de diagonales que tiene un polígono de n lados:
Para el decágono sustituimos n = 10 y se obtiene:
D = 10 x (10 – 3) /2 = 35
En el decágono regular, todas las diagonales se cortan en un punto, que es el centro de la figura:
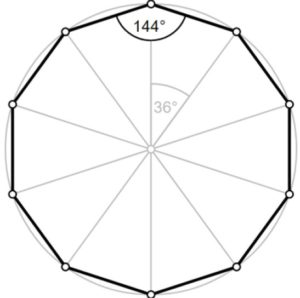
Se define el centro de un polígono como aquel punto equidistante de cualquier vértice. En la figura anterior, el centro coincide con el punto de intersección de todas las diagonales.
Si el decágono regular tiene lado a, su perímetro P es la suma de todos los lados:
P = 10.a
Conociendo la longitud a del lado, el área del decágono regular se calcula mediante:
Una fórmula aproximada para el área es:
Y una tercera opción para encontrar el área es mediante la longitud de la apotema LA. Este es el segmento que une el punto medio de un lado con el centro del polígono.
En tal caso el área se puede calcular mediante la fórmula:
El decágono irregular no es equilátero o equiángulo, y en líneas generales carece de la simetría de la figura regular, aunque algunos decágonos pueden tener eje de simetría.
También pueden ser convexos o cóncavos, si hay ángulos internos mayores de 180º.
El decágono irregular de la figura 1 es cóncavo, ya que algunos de sus ángulos internos son mayores de 180º. Es evidente que existen muchas combinaciones de ángulos y lados que dan lugar a un decágono irregular.
En todo caso, se cumple que:
-Los ángulos internos de un decágono irregular igualmente suman 1440º.
-Asimismo tiene 35 diagonales.
En general no hay una fórmula única para hallar el área de un polígono irregular, ya que los lados y los ángulos son diferentes. Sin embargo, se puede encontrar conociendo las coordenadas de los vértices y calculando los determinantes de Gauss:
-Llamemos (xn , yn ) a las coordenadas de los vértices, con n variando desde 1 hasta 10.
-Se puede empezar desde cualquier vértice, al cual se le asignarán las coordenadas (x1, y1 ). Ahora hay que sustituir los valores de cada coordenada en esta fórmula:
Donde los determinantes son precisamente las operaciones entre paréntesis.
-Es importante tomar nota de que el último determinante involucra de nuevo al primer vértice junto con el último. Para el decágono, quedaría así:
(x10y1 – x1y10)
Importante: Las barras son las de valor absoluto y significan que el resultado final se da con signo positivo siempre.
El procedimiento puede ser laborioso cuando la figura tiene muchos vértices, en el caso del decágono son 10 operaciones, por eso es recomendable hacer una tabla o una lista.
Calcular el área del decágono irregular mostrado en la figura. Las coordenadas de los vértices son A, B, C… J, cuyos valores se muestran a la izquierda.
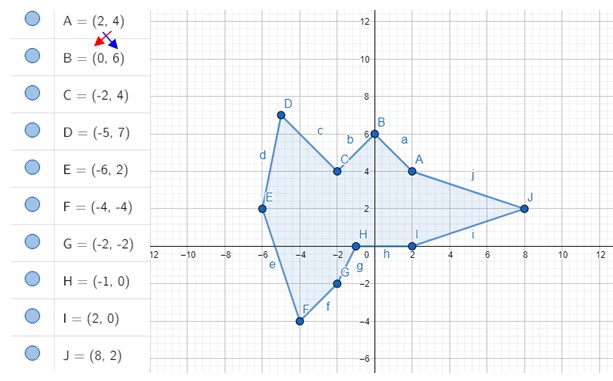
-Hacemos cada una de las 10 operaciones:
- 2×6 – 4×0 = 12 – 0 =12
- 0×4 – 6×(-2) = 0 + 12 =12
- (-2)×7- 4×(-5) = -14 + 20 = 6
- (-5)×2 – 7×(-6) = -10 + 42 = 32
- (-6)×(-4) – 2×(-4) = 24 + 8 =32
- (-4)×(-2) – (-4)×(-2) = 8 – 8 =0
- (-2)×0 – (-2)×(-1) =0 -2
- (-1)×0 – 0×(2) = 0 – 0 = 0
- 2×2 – 0×8 = 4 – 0 = 4
- 8×4 -2×2 = 32 – 4 = 28
-Sumamos los resultados:
12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124
Se obtiene un resultado positivo aún sin las barras de valor absoluto, pero en caso de ser negativo igual se cambia de signo.
-Se divide el resultado anterior entre 2 y esa es el área del polígono:
A=124/2 = 62
A continuación el resumen de las propiedades generales de un decágono, ya sea regular o irregular:
-Tiene 10 lados y 10 vértices.
-La suma de los ángulos internos es 1440º.
-Hay 35 diagonales.
-El perímetro es la suma de todos los lados.
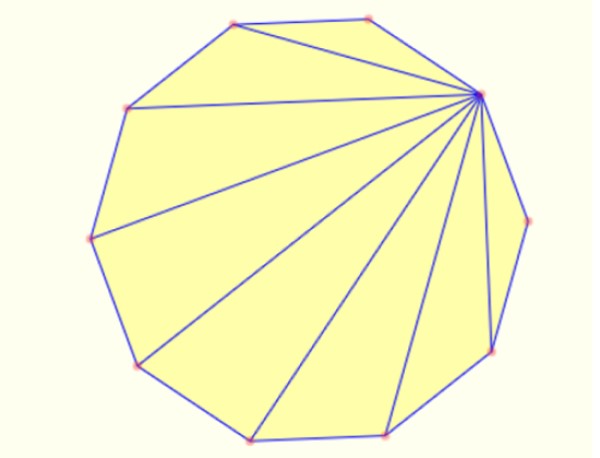
-Se pueden crear triángulos en el interior de un polígono dibujando segmentos desde un vértice hasta todos los demás. En un decágono es posible dibujar 8 triángulos de esta manera, como en el que se muestra a continuación:
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- Decágono.com. Decágono. Recuperado de: decagono.com
- Math Open Reference. Decagon. Recuperado de: mathopenref.com.
- Sangaku Maths. Elementos de un polígono y su clasificación. Recuperado de: sangakoo.com.
- Wikipedia. Decágono. Recuperado de: es.wikipedia.com.
