Distribución de frecuencias: cómo hacer una tabla, ejemplo, ejercicio
Una distribución de frecuencias en estadística se refiere a la tendencia que siguen los datos organizados en grupos, categorías o clases, cuando a cada una se le asigna un número denominado frecuencia, el cual indica cuántos datos hay en cada grupo.
Por regla general se observa que dichas frecuencias se distribuyen en torno a un grupo central: el que tiene el mayor número de datos.
Los grupos que están por encima o por debajo de dicha categoría central disminuyen gradualmente su frecuencia, siendo muy pequeña o insignificante para las categorías más alejadas de la categoría con frecuencia mayor.
La forma de conocer la distribución de frecuencias de un conjunto de datos consiste en primer lugar en crear las categorías y luego hacer la tabla de frecuencias. La representación visual de la tabla de frecuencias se denomina histograma.
Índice del artículo
- 1 Tipos de frecuencia
- 2 Pasos para hacer una tabla de distribución de frecuencias
- 3 Ejercicio resuelto
- 4 Referencias
Hay varios tipos de frecuencias:
1.- Frecuencia absoluta: es la más básica, y a partir de ella se construyen las demás. Consta simplemente del número total de datos correspondientes a una categoría.
2.- Frecuencia relativa: es la frecuencia absoluta de cada categoría dividida entre el número total de datos.
3.- Frecuencia porcentual: es la misma frecuencia relativa pero multiplicada por cien, indicando el porcentaje de aparición de valores en cada categoría.
4.- Frecuencia acumulada: es la suma de las frecuencias absolutas de las categorías inferiores o iguales a la categoría que se esté considerando.
5.- Frecuencia acumulada porcentual: es la sumatoria de las frecuencias porcentuales de las categorías inferiores o iguales a la categoría que se esté observando.
Son varios los pasos que deben seguirse para construir una tabla de distribución de frecuencias.
En primer lugar hay que disponer de los datos, los cuales pueden ser de variada índole: las edades de los niños de un colegio, el número de respuestas correctas en un test, la altura de los empleados de una empresa, el largo de las hojas de un árbol, etc.
Paso 1
Identificar el valor mínimo xmin y el valor máximo xmax en el conjunto de datos x.
Paso 2
Calcular el rango R, que se define como la diferencia entre el valor máximo menos el valor mínimo: R = xmax – xmin.
Paso 3
Determinar el número k de intervalos o clases, las cuales pueden estar preestablecidas. El número k determinará el número de filas que tendrá la tabla de frecuencias.
Paso 4
En caso de que el número de intervalos k no esté previamente dado, entonces debe establecerse de acuerdo a los siguientes lineamientos: el menor número de categorías recomendado es 5, pero puede ser mayor en cuyo caso es preferible elegir un número impar.
Paso 5
Hay una fórmula denominada regla de Sturges que nos da el número de intervalos k recomendado para un conjunto que consta de N datos:
k = [1 + 3,322⋅Log N]
Como el resultado dentro del corchete seguramente será un número real, el corchete nos indica que debe ser redondeado al entero impar más cercano para obtener un valor entero de k.
Paso 6
Se calcula la amplitud A de cada intervalo (clases o categorías) tomando el cociente entre el rango R y el número de intervalos k: A = R/k. Si los datos originales son números enteros, entonces A se redondea al entero más próximo, de lo contrario se deja su valor real.
Paso 7
Determinar los límites inferior Li y superior Ls de cada intervalo o clase. El primer intervalo, o la clase más baja, tiene como límite inferior Li el más pequeño de los datos originales, es decir Li = xmin y como límite superior el valor mínimo más la amplitud del intervalo, esto es Ls = xmin + A.
Paso 8
Los sucesivos intervalos son:
[xmin, xmin + A), [ xmin + A, xmin + 2⋅A), …, [ xmin + (k-1)A, xmin + k⋅A).
Paso 9
Se determina la marca de clase Xc para cada intervalo, mediante la siguiente fórmula: Xc = (Ls – Li) / 2 + Li.
Paso 10
Se coloca el encabezado de la tabla de frecuencia, el cual consta de una fila con las siguientes etiquetas: clases, marca de clase Xc, frecuencia f, frecuencia relativa fr (o frecuencia porcentual f%) y frecuencia acumulada F ( o frecuencia porcentual acumulada F%).
Lo que tendremos a continuación es lo siguiente:
Primera columna de la tabla de frecuencia: contiene los intervalos o clases en los que se han dividido los datos.
Segunda columna: contiene la marca de clase (o punto intermedio) de cada subintervalo.
Tercera columna: contiene la frecuencia absoluta f de cada clase o categoría.
Cuarta y quinta columna: se colocan los valores correspondientes a la frecuencia relativa (o porcentual) y a la frecuencia acumulada F (o acumulada porcentual).
Los siguientes datos corresponden a las respuestas acertadas de un cuestionario de 100 preguntas aplicado a un grupo de 52 estudiantes:
65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.
Seguiremos los pasos para construir la tabla de frecuencia:
1.- Valores mínimo y máximo Xmin = 1, Xmax = 89.
2.- El rango es: R = 89 – 1 = 88
3.- Determinación del número de intervalos de acuerdo a la regla de Sturges: k = [1 + 3,322⋅Log 52] = [ 6,70] = 7.
4.- Cálculo del ancho de los intervalos: A = R / k = 88 / 7 = 12,57 ≈ 13.
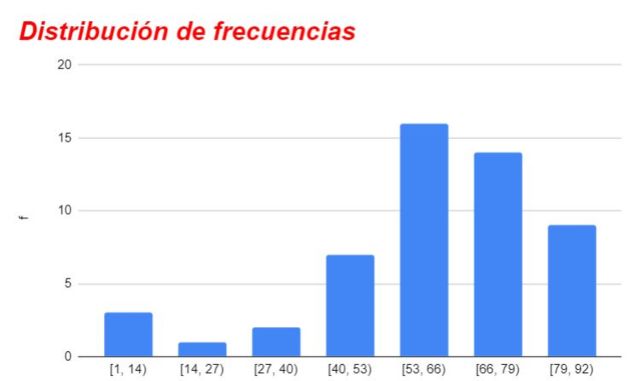
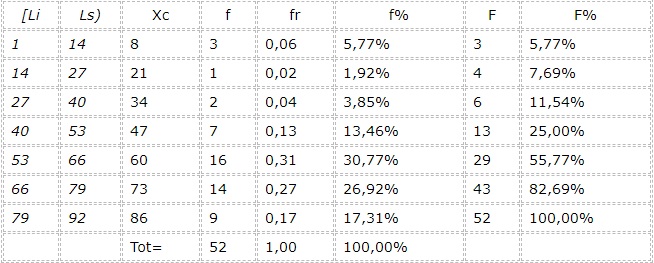
5.- Los intervalos son: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92).
6.- Se determinan las marcas de clase de cada intervalo: 8, 21, 34, 47, 60, 73 y 86.
7.- Se hace la tabla:
El gráfico de las frecuencias para los diferentes intervalos o categorías se muestra en la figura 1.
Un profesor registra el porcentaje de objetivos logrados en la asignatura de física para cada estudiante. Sin embargo, la calificación a cada estudiante, aunque depende del porcentaje de objetivos logrados, está ceñida a ciertas categorías previamente establecidas en el reglamento de estudios de la universidad.
Veamos un caso concreto: en una sección de física se tiene el porcentaje de objetivos logrados para cada uno de los 52 estudiantes:
15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 65, 70, 89, 64, 54, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.
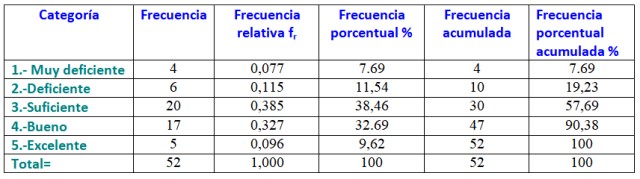
En este ejemplo las categorías o clases se corresponden con la calificación final que se asigna de acuerdo al porcentaje x de objetivos logrados:
1.- Muy deficiente: 1 ≤ x 30
2.- Deficiente: 30 ≤ x 50
3.- Suficiente: 50 ≤ x 70
4.- Bueno: 70 ≤ x 85
5.- Excelente: 85 ≤ x ≤ 100
Para hacer la tabla de frecuencias se procede a ordenar los datos de menor a mayor y se cuenta cuantos datos corresponden a cada categoría, la cual será la calificación que obtendrá el estudiante en la asignatura de física:
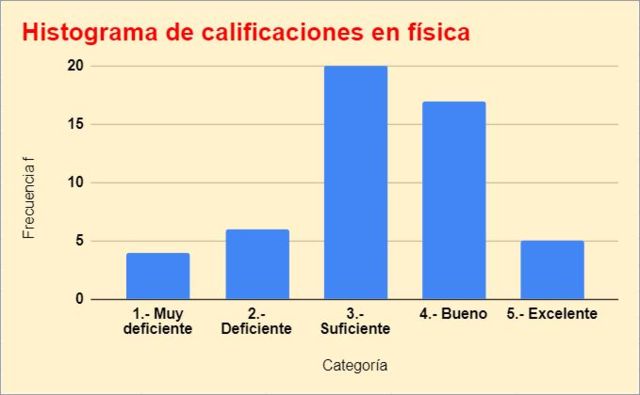
1.- Muy deficiente: 4 estudiantes.
2.- Deficiente: 6 estudiantes.
3.- Suficiente: 20 estudiantes.
4.- Bueno: 17 estudiantes.
5.- Excelente: 5 estudiantes.
A continuación se muestra el histograma de calificaciones, construido a partir de la tabla anterior:
- Berenson, M. 1985. Estadística para administración y economía. Interamericana S.A.
- Canavos, G. 1988. Probabilidad y Estadística: Aplicaciones y métodos. McGraw Hill.
- Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
- Levin, R. 1988. Estadística para Administradores. 2da. Edición. Prentice Hall.
- Spiegel, M. 2009. Estadística. Serie Schaum. 4 ta. Edición. McGraw Hill.
- Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.
