Matemáticas discretas: definición, para qué sirven, teoría de conjuntos
¿Qué son las matemáticas discretas?
Las matemáticas discretas corresponden a un área de la matemática que se encarga de estudiar el conjunto de los números naturales; es decir, el conjunto de números finitos e infinitos contables donde los elementos pueden ser contados por separado, uno por uno.
A esos conjuntos se les conoce como conjuntos discretos; un ejemplo de estos conjuntos son los números enteros, los grafos o expresiones lógicas, y son aplicados en diferentes campos de la ciencia, principalmente en la informática o computación.

Descripción
En la matemática discreta los procesos son numerables, tienen como base los números enteros. Esto significa que no son utilizados números decimales y, por lo tanto, tampoco es usada la aproximación o los límites, como en otras áreas. Por ejemplo, una incógnita puede ser igual a 5 o 6, pero nunca 4,99 o 5,9.
Por otra parte, en la representación gráfica las variables serán discretas y son dadas a partir de un conjunto finito de puntos, que son contados uno a uno, tal como se observa en la imagen:
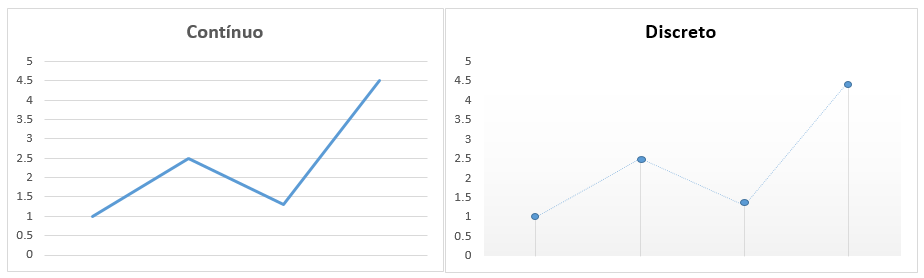
Las matemáticas discretas nacen por la necesidad de obtener un estudio exacto que pueda ser combinado y probado, para así aplicarlo en diferentes áreas.
¿Para qué sirven las matemáticas discretas?
La matemática discreta es utilizada en múltiples áreas. Dentro de las principales se encuentran las siguientes:
Combinatoria
Estudia conjuntos finitos donde los elementos pueden ser ordenados o combinados y recontados.
Teoría de distribución discreta
Estudia eventos que ocurren en espacios donde las muestras pueden ser contables, en los que las distribuciones continuas se usan para aproximarse las distribuciones discretas, o de manera contraria.
Teoría de la información
Se refiere a la codificación de información, usada para el diseño y transmisión y almacenamiento de datos, como por ejemplo señales análogas.
Informática
A través de la matemática discreta se resuelven problemas usando algoritmos, así como también se estudia lo que puede ser computado y el tiempo que tarda para hacerlo (complejidad).
La importancia de las matemáticas discretas en esta área se ha incrementado en las últimas décadas, sobre todo para el desarrollo de lenguajes de programación y de softwares.
Criptografía
Se basa en la matemática discreta para crear estructuras de seguridad o métodos de cifrado. Un ejemplo de esta aplicación son las contraseñas, enviando por separado bits que contienen información.
A través del estudio las propiedades de los números enteros y los números primos (teoría de los números) se pueden crear o destruir esos métodos de seguridad.
Lógica
Se usan estructuras discretas, que por lo general forman un conjunto finito, para así conseguir demostrar teoremas o, por ejemplo, verificar un software.
Teoría de los grafos
Permite la resolución de problemas lógicos, usando nodos y líneas que forman un tipo de gráfico, como se muestra en la siguiente imagen:
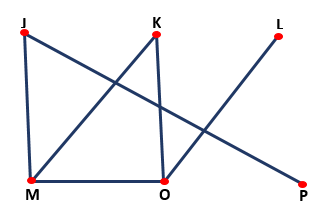
Es un área muy ligada a la matemática discreta porque las expresiones algebraicas son discretas. Por medio de esta se desarrollan circuitos electrónicos, procesadores, programación (álgebra Booleana) y bases de datos (álgebra relacional).
Geometría
Estudia las propiedades combinatorias de objetos geométricos, como por ejemplo, el recubrimiento del plano. Por otra parte, la geometría computacional hace posible desarrollar problemas geométricos aplicando algoritmos.
Teoría de los conjuntos
En las matemáticas discretas los conjuntos (finitos e infinitos numerables) son el principal objetivo de estudio. La teoría de los conjuntos fue publicada por George Cantor, quien demostró que todos los conjuntos infinitos tienen el mismo tamaño.
Un conjunto es una agrupación de elementos (números, cosas, animales y personas, entre otros) que son bien definidos; es decir, que existe una relación según la cual cada elemento pertenece a un conjunto, y se expresa, por ejemplo, a ∈ A.
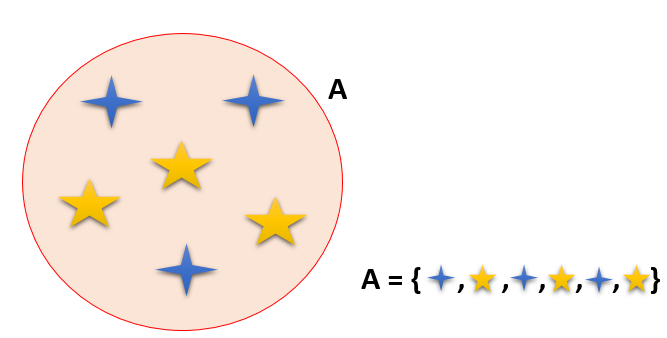
En matemática existen diferentes conjuntos que agrupan determinados números según sus características. Así, por ejemplo, se tienen:
– Conjunto de números naturales N = {0, 1, 2, 3, 4, 5, 6,…+∞}.
– Conjunto de números enteros E = {-∞…, -3, -2, -1, 0, 1, 2, 3,… +∞}.
– Subconjunto de números racionales Q* = {-∞…, – ¼, – ½, 0, ¼, ½,…∞}.
– Conjunto de números reales R = {-∞…, – ½, -1, 0, ½, 1,… ∞}.
Los conjuntos se nombran con letras del alfabeto, en mayúscula; mientras que los elementos se nombran en letras minúsculas, dentro de llaves ({}) y separados por comas (,). Generalmente son representados en diagramas como el de Venn y el de Caroll, así como también de forma computacional.
Con operaciones básicas como unión, intersección, complemento, diferencia y producto cartesiano, los conjuntos y sus elementos son manejados, basados en la relación de pertenencia.
Existen varias clases de conjuntos, los más estudiados en las matemáticas discretas son los siguientes:
Conjunto finito
Es aquel que tiene un numero finito de elementos y que corresponde a un número natural. Así, por ejemplo, A= {1, 2, 3,4} es un conjunto finito que tiene 4 elementos.
Conjunto infinito contable
Es aquel en el cual existe una correspondencia entre los elementos de un conjunto y los números naturales; es decir, que a partir de un elemento se pueden listar sucesivamente todos los elementos de un conjunto.
De esa manera, cada elemento va a corresponder con cada elemento del conjunto de los números naturales. Por ejemplo:
El conjunto de los números enteros Z = {…-2, -1, 0, 1, 2…} puede ser listado como Z = {0, 1, -1, 2, -2…}. De esa forma es posible realizar una correspondencia uno a uno entre los elementos de Z y los números naturales, como se aprecia en la siguiente imagen:
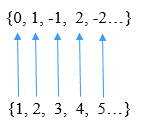
Es un método utilizado para solucionar problemas (modelos y ecuaciones) continuos que deben ser convertidos en problemas discretos, en los que la solución es conocida con la aproximación de la solución del problema continuo.
Visto de otra forma, la discretización trata de sacar una cantidad finita de un conjunto infinito de puntos; de esa forma, una unidad continua es transformada en unidades individuales.
Generalmente este método es usado en el análisis numérico, como por ejemplo en la solución de una ecuación diferencial, por medio de una función que está representada por una cantidad finita de datos en su dominio, aun cuando este es continuo.
Otro ejemplo de la discretización es su uso para convertir una señal análoga a digital, cuando unidades continuas de señal son convertidas en unidades individuales (son discretizadas), y luego codificadas y cuantificadas para obtener señal digital.
Referencias
- Grimaldi, R. P. (1997). Matemáticas discretas y combinatoria. Editorial Addison Wesley Iberoamericana.
- Ferrando, V. Gregori. (1995). Matemática discreta. Reverte.
- Jech, T. (2011). Set Theory. Stanford Encyclopedia of Philosophy.
- José Francisco Villalpando Becerra, A. G. (2014). Matemáticas Discretas: Aplicaciones y Ejercicios. Grupo Editorial Patria.
- Landau, R. (2005). Computing, A First Course in Scientific.
- Merayo, F. G. (2005). Matemática Discreta. Editorial Thomson.
- Rosen, K. H. (2003). Discrete Mathematics and its applications. Editorial McGraw-Hill.
- Schneider, D. G. (1995). A Logical Approach to Discrete Math.
