¿Existen triángulos escalenos con un ángulo recto?

Existen muchos triángulos escalenos con un ángulo recto. Antes de avanzar en el tema, es necesario primero conocer los diferentes tipos de triángulos que existen. Los triángulos se clasifican por dos clases que son: sus ángulos internos y las longitudes de sus lados.
La suma de los ángulos internos de cualquier triángulo es siempre igual a 180º. Pero de acuerdo a las medidas de los ángulos internos se clasifican en:
–Acutángulo: son aquellos triángulos tales que sus tres ángulos son agudos, es decir, que miden menos de 90° cada uno.
–Rectángulo: son aquellos triángulos que tienen un ángulo recto, es decir, un ángulo que mide 90°, y, por tanto, los otros dos ángulos son agudos.
–Obtusángulo: son los triángulos que tienen un ángulo obtuso, es decir, un ángulo cuya medida es mayor de 90°.
Triángulos escalenos con un ángulo recto
El interés en esta parte es determinar si un triángulo escaleno puede tener un ángulo recto.
Según lo dicho arriba, un ángulo recto es un ángulo cuya medida es 90º. Solo falta conocer la definición de un triángulo escaleno, la cual depende de la longitud de los lados de un triángulo.
Clasificación de los triángulos según sus lados
De acuerdo a la longitud de sus lados, los triángulos se clasifican en:
–Equilátero: son todos aquellos triángulos tales que las longitudes de sus tres lados son iguales.
–Isósceles: son los triángulos que poseen exactamente dos lados de igual longitud.
–Escaleno: son aquellos triángulos en los que los tres lados tienen medidas diferentes.
Formulación de una pregunta equivalente
Una pregunta equivalente a la del título es “¿Existen triángulos que tengan los tres lados con medidas diferentes y este tenga un ángulo de 90°?”
La respuesta como se dijo al comienzo es Sí. No es muy difícil justificar esta respuesta.
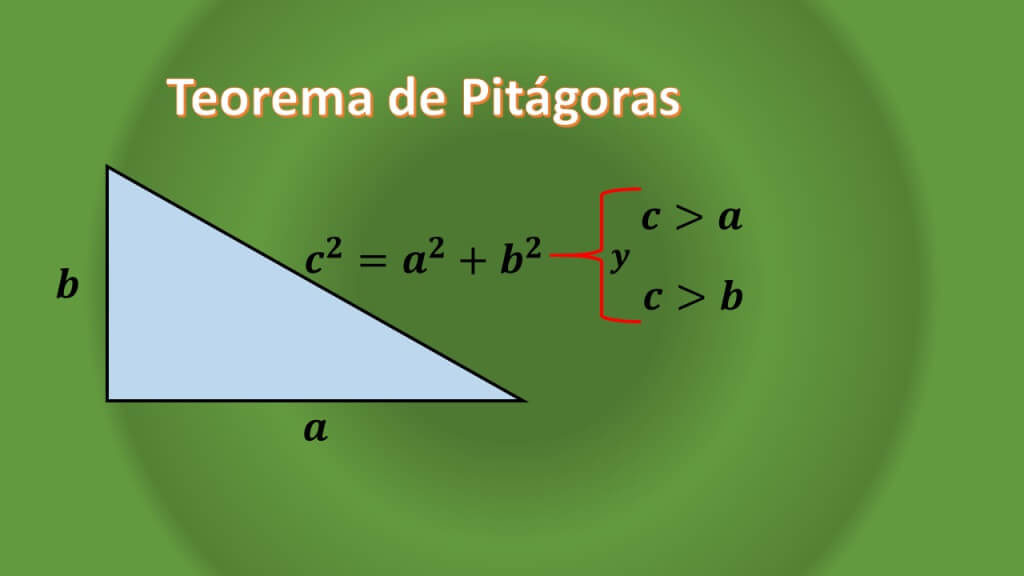
Si se observa con cuidado, ningún triángulo rectángulo es equilátero, esto se puede justificar gracias al teorema de Pitágoras para triángulos rectángulos, que dice:
Dado un triángulo rectángulo tal que las longitudes de sus catetos son “a” y “b”, y la longitud de su hipotenusa es “c”, se tiene que c²=a²+b², con lo cual se puede ver que la longitud de la hipotenusa “c” siempre es mayor que la longitud de cada cateto.
Como no se dice nada sobre “a” y “b”, entonces esto implica que un triángulo rectángulo puede ser Isósceles o Escaleno.
Entonces, solo basta escoger cualquier triángulo rectángulo tal que sus catetos tengan medidas diferentes, y así se habrá escogido un triángulo escaleno que tiene un ángulo recto.
Ejemplos
-Si se considera un triángulo rectángulo cuyos catetos tengan longitudes de 3 y 4 respectivamente, entonces por el teorema de Pitágoras se puede concluir que la hipotenusa tendrá una longitud de 5. Esto implica que el triángulo es escaleno y posee un ángulo recto.
-Sea ABC un triángulo rectángulo con catetos de medidas 1 y 2. Entonces la longitud de su hipotenusa es √5, con lo cual se concluye que ABC es un triángulo rectángulo escaleno.
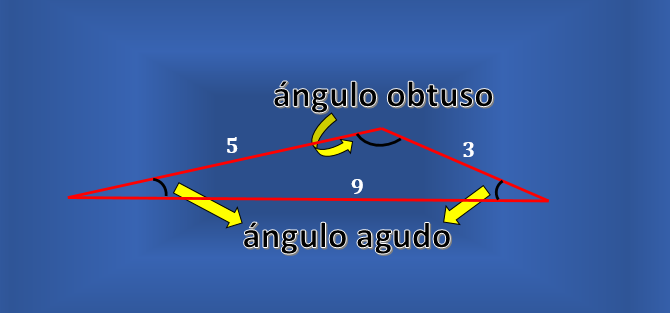
No todo triángulo escaleno posee un ángulo recto. Se puede considerar un triángulo como el de la siguiente figura, el cual es escaleno, pero ninguno de sus ángulos internos es recto.