Derivadas parciales: propiedades, cálculo, ejercicios

Las derivadas parciales de una función con varias variables independientes son las que se consiguen tomando la derivada ordinaria en una de las variables, mientras las otras se mantienen o se toman como constantes.

La derivada parcial en una de las variables, determina cómo varía la función en cada punto de misma, por unidad de cambio la variable en cuestión. 

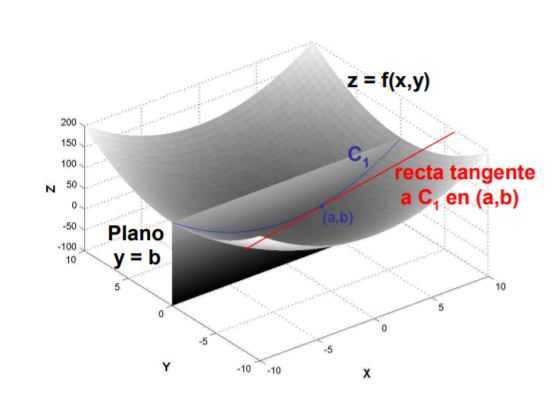
Por su definición, la derivada parcial, se calcula tomando el límite matemático del cociente entre la variación de la función y la variación de la variable respecto a la que se deriva, cuando el cambio de esta última tiende a cero.

Supongamos el caso de una función f que depende de las variables x e y, es decir para cada par (x, y) se asigna un z: 

f: (x,y) → z .

La derivada parcial de la función z = f(x, y), respecto de x se define como:

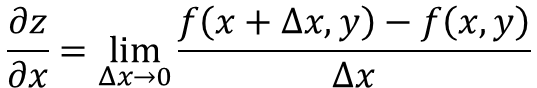
Ahora bien, hay varias maneras de denotar a la derivada parcial de una función, por ejemplo:

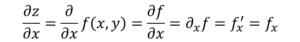
La diferencia con la derivada ordinaria, en cuanto a notación, es que la d de derivación se cambia por el símbolo ∂, conocido como “D de Jacobi”.

Índice del artículo

• 1 Propiedades de las derivadas parciales
  • 1.1 Continuidad
  • 1.2 Regla de la cadena
  • 1.3 Propiedad de cierre o cerradura
  • 1.4 Derivadas parciales sucesivas
  • 1.5 Teorema de Schwarz
• 2 ¿Cómo se calculan las derivadas parciales?
  • 2.1 Ejemplo 1
  • 2.2 Ejemplo 2
• 3 Ejercicios resueltos
  • 3.1 Ejercicio 1
  • 3.2 Ejercicio 2 
• 4 Referencias

Propiedades de las derivadas parciales

La derivada parcial de una función de varias variables, respecto de una de ellas, es la derivada ordinaria en dicha variable y considerando al resto como fijas o constantes. Para hallar la derivada parcial, se pueden usar las reglas de derivación de las derivadas ordinarias.

A continuación las principales propiedades:

Continuidad

Si una función f(x, y) tiene derivadas parciales en x e y en el punto (xo, yo) entonces puede decirse que la función es contínua en ese punto.

Regla de la cadena

Una función f(x,y) con derivadas parciales continuas en x e y, que a su vez depende de un parámetro t a través de x=x(t) y y=y(t), tiene derivada ordinaria respecto de la variable t, la cual se calcula mediante la regla de la cadena:

d_t z = ∂_xz d_tx + ∂_yz d_ty

Propiedad de cierre o cerradura

La derivada parcial respecto a una de las variables de una función f de dos o más variables (x, y, …), es otra función g en esas mismas variables, por ejemplo: 

g(x, y, …) = ∂_y f(x, y, …)

Es decir, la derivación parcial es una operación que va de Rⁿ a Rⁿ. En ese sentido se dice que es una operación cerrada.

Derivadas parciales sucesivas

Se pueden definir las derivadas parciales sucesivas de una función de varias variables, dando lugar a nuevas funciones en las mismas variables independientes.

Sea la función f(x,y). Se pueden definir las siguientes derivadas sucesivas:

f_xx = ∂_xf ;  f_yy = ∂_yyf ; f_xy = ∂_xyf y f_yx = ∂_yxf

Las dos últimas se conocen como derivadas mixtas porque involucran dos variables independientes diferentes.

Teorema de Schwarz

Sea una función f(x,y), definida de tal manera que sus derivadas parciales son funciones continuas en un subconjunto abierto de R².

Entonces, para todos y cada uno de pares (x, y) que pertenezcan a dicho subconjunto, se tiene que las derivadas mixtas son idénticas:

∂_xyf = ∂_yxf

El enunciado anterior se conoce como teorema de Schwarz.

¿Cómo se calculan las derivadas parciales?

Las derivadas parciales se calculan de forma similar a las derivadas ordinarias de funciones en una sola variable independiente. Cuando se toma la derivada parcial de una función de varias variables con respecto a una de ellas, las otras variables se toman como constantes.

A continuación se dan varios ejemplos:

Ejemplo 1

Sea la función:

f(x,y) = -3x² + 2(y – 3)²

Se pide calcular la primera derivada parcial con respecto a x y la primera derivada parcial con respecto a y.

Procedimiento

Para calcular la parcial de f respecto de x, se toma y como constante:

∂_xf = ∂_x( -3x² + 2(y – 3)² ) = ∂_x( -3x² )+ ∂_x( 2(y – 3)² ) = -3 ∂_x(x²) + 0 = -6x.

Y a su vez, para calcular la derivada con respecto a y se toma x como constante:

∂_yf = ∂_y( -3x² + 2(y – 3)² ) = ∂_y( -3x² )+ ∂_y( 2(y – 3)² ) = 0 + 2·2(y – 3) = 4y – 12.

Ejemplo 2

Determinar las derivadas parciales de segundo orden:  ∂_xxf, ∂_yyf, ∂_yxf y ∂_xyf para la misma función f del ejemplo 1.

Procedimiento

En este caso, como ya está calculada la primera derivada parcial en x e y (ver ejemplo 1):

∂_xxf = ∂_x(∂_xf) = ∂_x(-6x) = -6

∂_yyf = ∂_y(∂_yf) = ∂_y(4y – 12) = 4

∂_yxf = ∂_y(∂_xf) = ∂_y(-6x) = 0

∂_xyf = ∂_x(∂_yf) = ∂_x(4y – 12) = 0

Se observa que ∂_yxf = ∂_xyf, cumpliéndose así el teorema de Schwarz, dado que la función f y sus derivadas parciales de primer orden son todas funciones continuas en R².

Ejercicios resueltos

Ejercicio 1

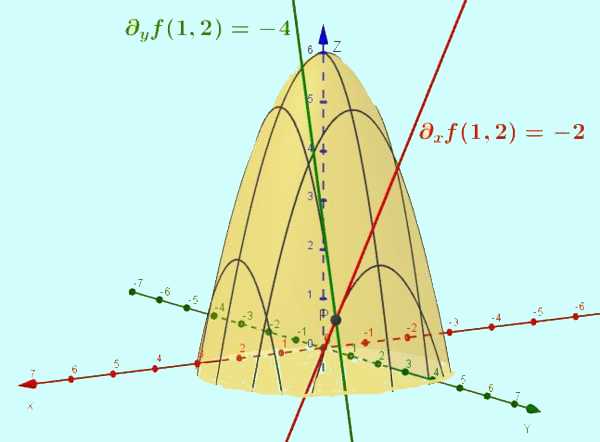
Sea la función:

f(x,y) = -x² – y² + 6

Hallar las funciones g(x,y) = ∂_xf  y h(x,y) = ∂_yf.

Solución

Se toma la derivada parcial de f respecto de x, para lo cual la variable y se hace constante:

g(x, y) = – 2x

De forma semejante, se toma la derivada parcial de g respecto de y, haciendo x constante, resultando para la función h:

h(x, y) = -2y

Ejercicio 2 

Evalúe para el punto (1, 2) las funciones f(x, y) y g(x, y) del ejercicio 1. Interprete los resultados.

Solución

Se sustituyen los valores x=1 e y=2 obteniéndose:

f(1,2) = -(1)² -(2)² + 6= -5 + 6 = 1

Este es el valor que toma la función f cuando se evalúa en ese punto.

La función f(x,y) es una superficie bidimensional y la coordenada z=f(x,y) es la altura de la función para cada par (x,y). Cuando se toma el par (1,2), la altura de la superficie f(x,y) es z = 1.

La función g(x, y) = – 2x representa a un plano en el el espacio tridimensional cuya ecuación es z = -2x o bien -2x + 0 y -z =0.

Dicho plano es perpendicular al plano xz y pasa por el punto (0, 0, 0). Cuando se evalúa en x=1 e y=2 entonces z = -2. Nótese que el valor z=g(x,y) es independiente del valor asignado a la variable y.

Por otra parte, si se intersecta la superficie f(x, y) con el plano y= c, con c constante, se tiene una curva en el plano zx: z = -x² – c² + 6.

En este caso la derivada de z respecto de x coincide con la derivada parcial de f(x,y) respecto de x: d_x z =  ∂_x f .

Al evaluar en el par (x=1, y=2) la derivada parcial en ese punto ∂_x f(1,2) se interpreta como la pendiente de la recta tangente a la curva z= -x² + 2 en el punto (x=1, y=2) y el valor de dicha pendiente es -2.

Referencias

1. Ayres, F. 2000. Cálculo. 5ed. Mc Graw Hill.
2. Derivadas parciales de una función en varias variables. Recuperado de: edificacion.upm.es.
3. Leithold, L. 1992. Cálculo con Geometría Analítica. HARLA, S.A.
4. Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Cálculo. México: Pearson Educación.
5. Gorostizaga J. C. Derivadas Parciales. Recuperado de: ehu.eus
6. Wikipedia. Derivada parcial. Recuperado de: es.wikipedia.com.