Número de Euler o número e: cuánto vale, propiedades, aplicaciones
El número de Euler o número e es una conocida constante matemática que aparece con frecuencia en numerosas aplicaciones científicas y económicas, junto con el número π y otros números importantes en matemática.
Una calculadora científica arroja el siguiente valor para el número e:

e = 2.718281828…
Pero se conocen muchos más decimales, por ejemplo:
e = 2.71828182845904523536…
Y las computadoras modernas han permitido hallar trillones de decimales para el número e.
Se trata de un número irracional, lo cual significa que tiene una cantidad infinita de decimales sin ningún patrón repetitivo (la secuencia 1828 aparece dos veces al principio y ya no se repite más).
Y también quiere decir que el número e no puede obtenerse como el cociente de dos números enteros.
Índice del artículo
El número e fue identificado por el científico Jacques Bernoulli en 1683 cuando estudiaba el problema del interés compuesto, pero con anterioridad había aparecido de forma indirecta en los trabajos del matemático escocés John Napier, quien inventó los logaritmos hacia 1618.
Sin embargo, fue Leonhard Euler en 1727 quien le dio el nombre de número e y estudió intensivamente sus propiedades. Por eso también se lo conoce como el número de Euler y también como base natural para los logaritmos neperianos (un exponente) usados actualmente.
El número e vale:
e = 2.71828182845904523536…
Los puntos suspensivos significan que hay una cantidad infinita de decimales y de hecho, con las computadoras actuales se conocen millones de ellos.
Hay varias formas de definir a e que describimos seguidamente:
El número e como un límite
Una de las diversas formas en que se expresa el número e es la que el científico Bernoulli encontró en sus trabajos sobre el interés compuesto:
En la cual hay que hacer al valor n un número muy grande.
Es fácil comprobar, con ayuda de una calculadora, que cuando n es muy grande, la expresión anterior tiende al valor de e dado más arriba.
Claro que podemos preguntarnos qué tan grande puede hacerse n, así que probemos con números redondos, como estos por ejemplo:
n = 1000; 10.000 o 100.000
En el primer caso se obtiene e = 2.7169239…. En el segundo e = 2.7181459… y en el tercero se acerca mucho más al valor de e: 2.7182682. Ya nos podemos figurar que con n = 1.000.000 o más grandes, la aproximación será todavía mejor.
En lenguaje matemático, el procedimiento de hacer que n se acerque cada vez más a un valor muy grande, se llama límite al infinito y se denota así:
Para denotar al infinito se utiliza el símbolo “∞”.
El número e como una sumatoria
También es posible definir al número e mediante esta operación:
Las cifras que aparecen en el denominador: 1, 2, 6, 24, 120… corresponden a la operación n!, donde:
n! = n. (n-1).(n-2). (n-3)…
Y por definición 0! = 1.
Es fácil comprobar que cuantos más sumandos se agreguen, con mayor precisión se llega al número e.
Hagamos algunas pruebas con la calculadora, agregando cada vez más sumandos:
1 +1+ (1/2) + (1/6) = 2.71667
1 +1+ (1/2) + (1/6) + (1/24) = 2.75833
1 +1+ (1/2) + (1/6) + (1/24) + (1/120) = 2.76667
1 +1+ (1/2) + (1/6) + (1/24) + (1/120) + (1/720) = 2.71806
Mientras más términos se agreguen a la sumatoria, más se parece el resultado a e.
Los matemáticos idearon una notación compacta para estas sumas que involucran muchos términos, utilizando el símbolo de sumatoria Σ:
Esta expresión se lee así “sumatoria desde n = 0 hasta infinito de 1 entre n factorial”.
El número e desde el punto de vista geométrico
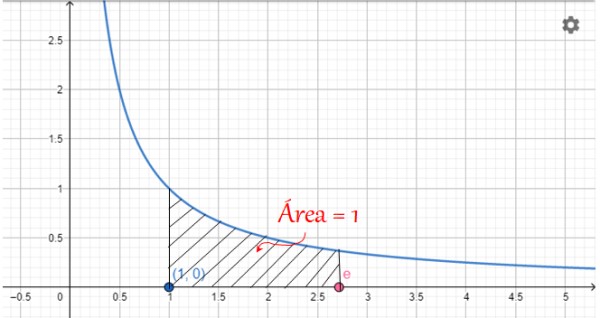
El número e tiene una representación gráfica relacionada con el área bajo la gráfica de la curva:
y = 1/x
Cuando los valores de x están comprendidos entre 1 y e, esta área vale 1, como se ilustra en la siguiente figura:
Algunas de las propiedades del número e son:
-Es irracional, en otras palabras, no puede obtenerse simplemente dividiendo dos números enteros.
-El número e también es un número trascendente, lo que quiere decir que e no es solución de ninguna ecuación polinomial.
-Está relacionado con otros cuatro números famosos en el ámbito de las matemáticas, a saber: π, i, 1 y 0, a través de la identidad de Euler:
eπi + 1 = 0
-Los llamados números complejos pueden expresarse a través de e.
-Constituye la base de los logaritmos naturales o neperianos de la actualidad (la definición original de John Napier difiere un poco).
-Es el único número tal que su logaritmo neperiano vale 1, es decir:
ln e = 1
El número e aparece con mucha frecuencia en el campo de la probabilidad y la estadística, apareciendo en diversas distribuciones, como la normal o gaussiana, la de Poisson y otras.
En ingeniería es frecuente, ya que la función exponencial y = ex está presente en mecánica y electromagnetismo, por ejemplo. Entre las muchas aplicaciones podemos citar:
-Un cable o cadena que cuelga sujeto por los extremos, adopta la forma de la curva dada por:
y = (ex + e-x) /2
-Un condensador C inicialmente descargado, que se conecta en serie a una resistencia R y una fuente de voltaje V para cargar, adquiere una cierta carga Q en función del tiempo t dada por:
Q (t) = CV (1-e-t/RC)
La función exponencial y = A.eBx, con A y B constantes, se utiliza para modelar el crecimiento de las células y el crecimiento bacteriano.
En física nuclear se modela el decaimiento radiactivo y la determinación de edades mediante fechado por radiocarbono.
En el cálculo del interés compuesto el número e surge de manera natural.
Supongamos que se tiene una cierta cantidad de dinero Po, para invertirlo a una tasa de interés del i % anual.
Si se deja el dinero durante 1 año, al cabo de ese tiempo se tendrá:
P (1 año) = Po + Po.i = Po (1+ i)
Tras otro año sin tocarlo, se tendrá:
P (2 años) = Po + Po.i + (Po + Po .i)i = Po +2Po.i + Po.i2 = Po (1+i)2
Y siguiendo de esta manera por n años:
P = Po (1+i)n
Ahora recordemos una de las definiciones de e:
Se parece un poco a la expresión para P, así que debe haber una relación.
Vamos a repartir la tasa de interés nominal i en n períodos de tiempo, de esta manera la tasa de interés compuesto será i/n:
P = Po [1+(i/n)]n
Esta expresión se parece un poco más a nuestro límite, pero todavía no es exactamente igual.
Sin embargo, después de algunas manipulaciones algebraicas se puede demostrar que haciendo este cambio de variable:
h = n/i → i = n/h
Nuestro dinero P se transforma en:
P = Po [1+(1/h)]hi = Po {[1+(1/h)]h}i
Y lo que está entre las llaves, aunque esté escrito con la letra h, es igual al argumento del límite que define al número e, faltando solo tomar el límite.
Hagamos h →∞, y lo que está entre las llaves se transforma en el número e. Esto no significa que tengamos que esperar un tiempo infinitamente grande para retirar nuestro dinero.
Si nos fijamos bien, al hacer h= n/i y tendiendo a ∞, lo que hemos hecho en realidad es repartir la tasa de interés en períodos de tiempo muy, muy pequeños:
i = n/h
Esto se llama capitalización continua. En tal caso la cantidad de dinero se calcula fácilmente así:
P = Po .ei
Donde i es la tasa de interés anual. Por ejemplo, al depositar 12 € al 9 % anual, mediante capitalización continua, al cabo de un año se tiene:
P = 12 x e0.09×1 € = 13.13 €
Con una ganancia de 1.13 €.
- Disfruta las matemáticas. Interés compuesto: Composición periódica. Recuperado de: disfrutalasmatematicas.com.
- Figuera, J. 2000. Matemática 1ro. Diversificado. ediciones CO-BO.
- García, M. El número e en el cálculo elemental. Recuperado de: matematica.ciens.ucv.ve.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Larson, R. 2010. Cálculo de una variable. 9na. Edición. McGraw Hill.
